vÒ mét c¸ch t×m gi¸ trÞ lín nhÊt , nhá nhÊt cña biÓu thøc
chøa hai biÕn sè
§ç B¸ Chñ – Th¸i B×nh tÆng www.mathvn.com
Có nhiều phương pháp để tìm giá trị lớn nhất (GTLN) , giá trị nhỏ nhất (GTNN) của một biểu thức có
từ một biến số trở lên . Bài viết này chúng tôi xin trao đổi về phương pháp tìm cực trị của biểu thức hai
biến số nhờ miền giá trị , trong đó hai biến bị ràng buộc bởi một điều kiện cho trước .
Bài toán : Cho các số thực x , y thoả mãn điều kiện : G(x ; y) = 0 ( hoặc G(x;
y
)0≥
hoặc G(x;
y
)0≤ ) .
Tìm GTLN , GTNN ( nếu có ) của biểu thức P = F(x ; y).
Cách giải :
Gọi T là miền giá trị của P . Khi đó m là một giá trị của T khi và chỉ khi hệ sau có nghiệm (x ; y):
(;) 0
(;)
=
⎧
⎨=
⎩
Gxy
F
xy m
( hoặc (;) 0
(;)
≥
⎧
⎨
=
⎩
Gxy
F
xy m
hoặc (;) 0
(;)
≤
⎧
⎨
=
⎩
Gxy
F
xy m
)
Sau đó tìm các giá trị của tham số m để một trong các hệ trên có nghiệm . Từ đó suy ra miền giá trị
T của P , rồi suy ra GTLN , GTNN ( nếu có ) của P.
Sau đây là các bài toán minh hoạ .
Bài toán 1 : Cho hai số thực x , y thoả mãn điều kiện :
(
)
33 33 3
(1) 1
x
xyy−+ −=xy
Tìm GTLN , GTNN của biểu thức =++
333
F
xyxy
.
Lời giải : Gọi T1 là miền giá trị của F . Ta có 1
mT
∈
⇔hệ sau có nghiệm:
(
)
33 33 3
333
(1) 1
xyy
xyxym
⎧−+ −=
⎪
⎨
⎪++ =
⎩
xy
Đặt :
33
3
S
xy
Pxy
⎧=+
⎪
⎨=
⎪
⎩
. Ta có 2
,,:4
x
ySPS∃⇔∃ ≥P
Hệ trên
22
30 23
S
SP S Sm
S
Pm PmS
⎧⎧
−− = + =
⇔⇔
⎨⎨
+= =−
⎩⎩
Ta có :
2
22 2
4( )
440
3
SS
SPS SS S
−
≥⇔≥ ⇔−≤⇔≤≤04
Từ đó hệ PT đầu có nghiệm ⇔2
() 2 3
f
SS S m=+= có nghiệm 0S4
≤
≤. Vì hàm bậc hai f(S) đồng
biến trên
[
]
0;4 nên PT f(S) = 3m có nghiệm 04S
≤
≤ (0) 3 (4) 0 3 24fmf m
⇔
≤≤ ⇔≤≤
. Do đó
0m⇔≤ ≤8
[
]
10;8T=
Vậy minF = 0 , maxF = 8.
Bài toán 2 : Cho các số thực x, y thoả mãn : 3
≤
22
x-xy+y
Tìm GTLN , GTNN của biểu thức 22
Q = x + x
y
-2
y
Lời giải : Gọi T2 là miền giá trị của Q . Ta có 2
mT
∈
⇔hệ sau có nghiệm:
3
⎧≤
⎨
⎩
22
22
x-xy+y (1)
x+xy-2y=m (2)
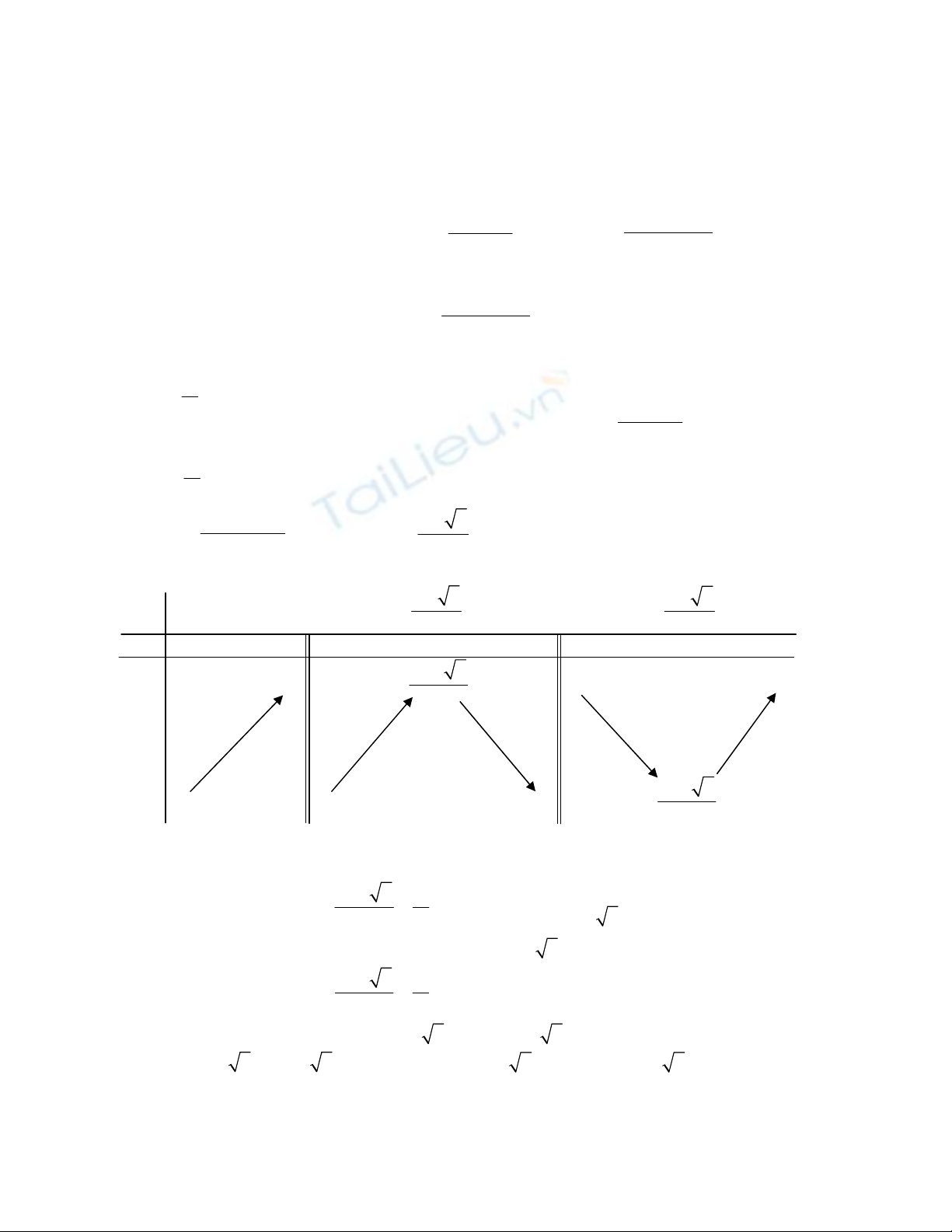
Nếu y = 0 thì hệ (1),(2) ⎧≤
⎪
⇔⎨=
⎪
⎩
2
2
3x
x
m
, suy ra trường hợp này hệ có nghiệm (x ; 0) ⇔≤
≤03m
Nếu y 0 thì đặt x = ty ta có hệ :
≠⎧−+ ≤
⎨+− =
⎩
22
22
(1)3(
(2) (
yt t
yt t m
3)
4)
2)tt+−Từ (4) ta phải có m( > 0 và thay
22
22
m
ytt
=
+
− vào (3) được −+ ≤
+−
2
2
(1)
3
2
mt t
tt
Trường hợp này hệ (1),(2) có nghiệm
⎧+−
⎪
⇔⎨−+
≤
⎪+−
⎩
2
2
2
m( 2) > 0
Ö(1)
3
2
tt
Hmt t
tt
có nghiệm
⎡>
⎧
⎪
⎢⎨
⎢≤ ∈ −∞ − ∪ +∞
⎪
⎢⎩
⇔⎢<
⎧
⎢⎪
⎢⎨≥∈−
⎢⎪
⎩
⎣
0
3
() ã Ö ( ; 2) (1; )
0
3
() ã Ö ( 2;1)
m
ft c nghimt
m
m
ft c nghimt
m
( I ) ( với
−
+
=
+
−
2
2
1
() 2
tt
ft tt ,
{
}
\2;1t∈−R )
Ta có : −+
′=+−
2
22
26
() (2
1tt
ft tt ()
)
, t
′=0±
⇔=
37
2
t
f
Bảng biến thiên của hàm f(t)
t −∞ - 2 −37
2 1 37
2
+ +
∞
f’(t) + + 0 - - 0 +
−127
9 +
∞
1 + ∞
f(t)
1 −∞
−
∞ 12
7
9
+
Từ bảng biến thiên ta có
( I )
⎡>
⎧
⎪
⎢⎨+
⎢≤
⎪
⎢⎡
<≤−+
⎩
⇔⇔
⎢⎢
<
⎧
−
−≤<
⎢⎢
⎣
⎪
⎢⎨−
⎢≥
⎪
⎢⎩
⎣
0
122 3
012
9
0127 0
127 3
9
m
m
m
mm
m
7
Kết hợp các trường hợp trên ta được : −− ≤ ≤−+127 127m.
Do đó ⎡⎤
=−− −+
⎣⎦
3127;127T . Vậy minQ = 127−− , maxQ = 127−+
( Bài này các bạn có thể tham khảo hướng dẫn giải đề số 4 - THTT tháng 6/2007 )
Bài toán 3 : Cho hai số thực x, y thoả mãn : 22
916683(18)
x
yxy xy+++≤−
Tìm GTNN của biểu thức
=
++ +(1)(1Kxx yy )
Lời giải : Gọi T3 là miền giá trị của K . Ta có mT
3
∈
⇔
)
hệ sau có nghiệm:
22
916683(18
(1)(1)
x
yxy xy
xx yy m
⎧+++≤−
⎨++ +=
⎩
Hệ trên
⎧−≤ + ≤
⎧
+++−≤
⎪⎪
⇔⇔
⎨⎨
+++=+
+++=+
⎪⎪
⎩
⎩
2
22
22
33 4 1 (5)
(3 4 ) 2(3 4 ) 3 0
111
111
()() (6)
()() 222
222
xy
xy xy
xym
xym
Dễ thấy : nếu 1
2
m thì hệ vô nghiệm
≤−
Với 1
2
m , xét trong mặt phẳng toạ độ Oxy ta có : tập hợp nghiệm của (5) là miền mặt phẳng
>−
(H) ở giữa hai đường thẳng song song 1:3 4 3 0dxy
+
+= và dx
2:3 4 1 0
+
y−= có chứa cả biên là hai
đường thẳng và , còn tập hợp nghiệm của (6) là đường tròn (C) có tâm I(
1
d2
d1
2
−;1
2
−) , bán kính
1
2
Rm=+
. Trường hợp này hệ (5),(6) có nghiệm
⇔
(C) và (H) có điểm chung
⇔
1
11
(; ) 10 2 100
dId R m m≤⇔ ≤ +⇔≥−
49
( thoả mãn m > 1
2
−
) .
Do đó 3
49 ;
100
T⎡⎞
=− +∞
⎟
⎢
⎣⎠
. Vậy =− 49
min 100
K ( không tồn tại maxK) .
(Bạn đọc tự vẽ hình minh hoạ).
Bài toán 4 : Cho các số thực x, y thoả mãn : 2cos 2cos 3 cos cos 2 cos cos
(2 .
) 2 4 42
x y xy xy++ ++ +
+−≥
Tìm GTLN , GTNN của biểu thức : cos 2 cos 2
M
xy
=
+
Lời giải : Gọi T4 là miền giá trị của M . Ta có
∈
⇔
4
mT hệ sau có nghiệm:
2cos 2cos 3 cos cos 2 cos cos
(2) 2 4 42
(*)
cos 2 cos 2
x y xy xy
xym
++ ++ +
⎧+−≥
⎪
⎨+=
⎪
⎩
Hệ(*) ⇔
cos cos 2 cos cos cos cos
22 22 22
3
1cos cos
(2 ) (22 2)2 42 0 2 2 22 2
22
2
cos cos cos cos cos cos
++ +
⎧⎧
⎧≤+≤
−+ +≤ ≤ ≤
⎪⎪
⎪⎪⎪
⇔⇔
⎨⎨⎨
++
22
2
+
+= +=
⎪⎪⎪
+=
⎩⎪
⎩
xy xy xy xy
mm
m
xy xy xy
vy==
⎪
⎩
Đặt ux ta có hệ :
cos ; cos
22
3
1(
2
1, 1 (8)
2(9)
2
⎧≤+≤
⎪
⎪≤≤
⎨
⎪+
⎪+=
⎩
uv
uv
m
uv
7)
v
Hệ (*) có nghiệm hệ (7),(8),(9) có nghiệm. ⇔
Dễ thấy , với m hệ (7),(8),(9) vô nghiệm .
2≤−
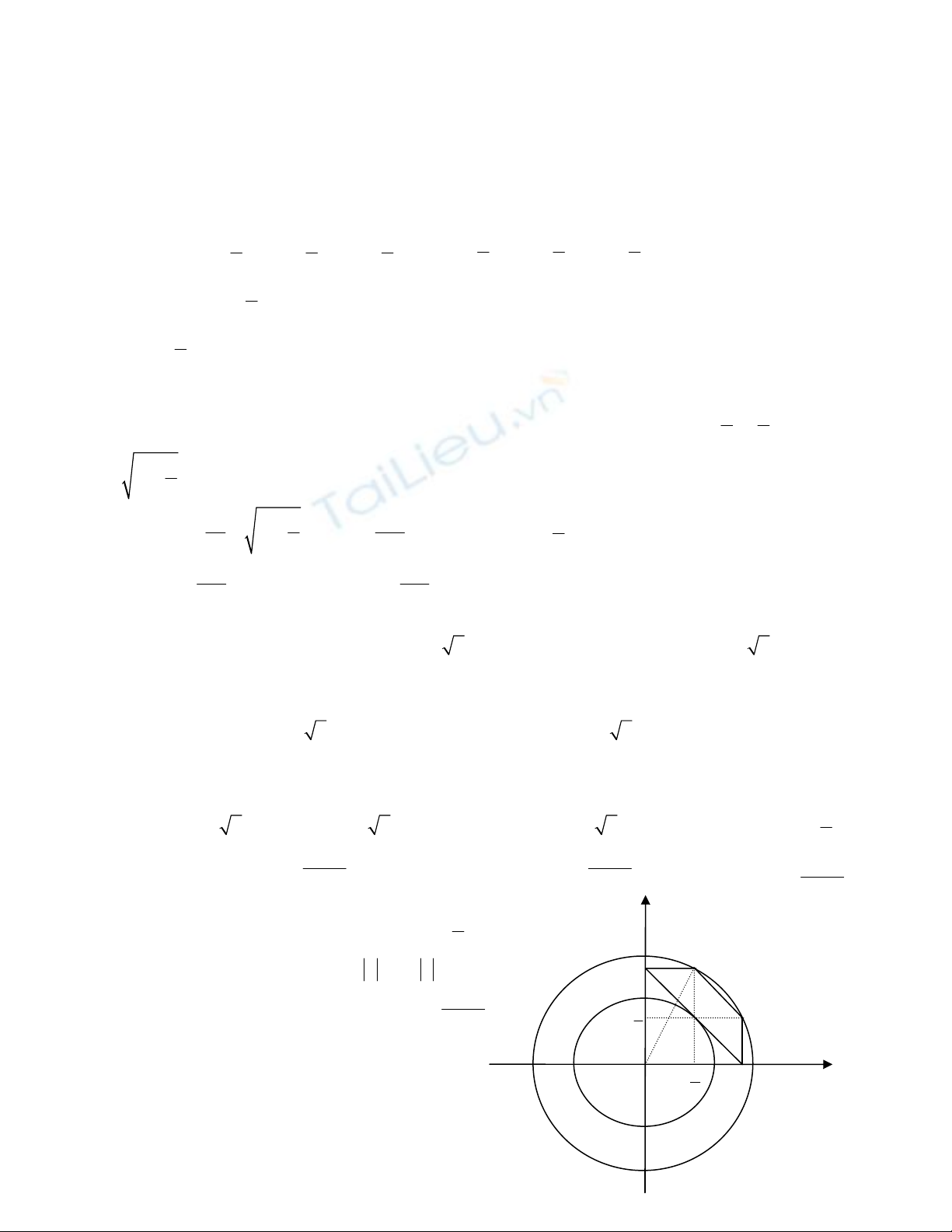
Với m > - 2 , xét trong mặt phẳng toạ độ Ouv
khi đó tập hợp nghiệm của (7) và (8) là hình
O u
A
B
C
D
1
1
1
2
1
2
thang cân ABCD ( gồm các điểm ở trong hình
thang và các điểm trên cạnh hình thang) , còn
tập hợp nghiệm của (9) là đường tròn ( T ) có
tâm O(0 ; 0) , bán kính 2
2
+
=m
R ( hình vẽ )
Từ đó , hệ (7),(8),(9) có nghiệm đường tròn ⇔
( T ) có điểm chung với hình thang ABCD
(; )dOCD R OB⇔≤≤
225
1
222
+
⇔≤ ≤⇔−≤≤
mm1
2
0
( thoả mãn m > - 2)
(Ở đây đường thẳng CD: , đường thẳng AB:
10uv+−= 223uv
+
−=và các tam giác OCD , OAB
cân tại O) .
Do đó 4
1
1; 2
⎡
=−
⎢
⎣⎦
T⎤
⎥
. Vậy minM = -1 , maxM = 1
2
Bài toán 5 : (Tuyển sinh đại học khối A năm 2006 )
Cho hai số thực thay đổi x
≠
0 , y
≠
0 thoả mãn : 22
(x y)xy x y xy
+
=+−
Tìm giá trị lớn nhất của biểu thức 33
11
Axy
=+
Lời giải : Gọi T5 là tập giá trị của A . Ta có 5
mT
∈
⇔hệ sau có nghiệm x
≠
0 , y 0 :
≠
22 22
22
22 2
33 33
(x y)xy x y xy (x y)xy x y xy
(x y)xy x y xy
11 (x y)(x y xy) xy(x y)
mmm
xy (xy) (xy)
⎧⎧
+
=+− + =+−
⎧+=+−
⎪⎪ ⎪
⇔⇔
⎨⎨ ⎨
++− +
+= ==
⎪⎪ ⎪
⎩⎩⎩
2
2
(x y)xy (x y) 3xy
xy
()m
xy
⎧+=+−
⎪
⇔+
⎨=
⎪
⎩
(V)
Đặt ( ) , ta có hệ :
Sxy
Pxy
=+
⎧
⎨=
⎩
2
S4≥P
2
2
SP S 3P
S
() m
P
⎧
=
−
⎪
⎨=
⎪
⎩
(VI)
Hệ (V) có nghiệm x 0 , y 0 hệ (VI) có nghiệm ( S ; P ) thoả mãn .
≠ ≠ ⇔2
S4P≥
Do 22 2 2
13
SP x y xy (x y) y 0
24
=+−=− + >
với mọi x
≠
0 , y
≠
0 S0
P
⇒>
với mọi x 0 , y
≠
≠
0
Từ đó :
• Nếu thì hệ (V) vô nghiệm
m0≤
• Nếu m > 0 thì từ phương trình 2
SS
() m m
PP
=⇒= Sm.⇒= P
thay vào phương trình
đầu của hệ (VI) được : 22
mP mP 3P (m m)P 3=−⇔− = ( vì SP > 0 nên P 0 )
≠
Để có P từ phương trình này thì mm0m1
−
≠⇔ ≠
( m > 0 ) và ta được
3
Pm( m 1)
=− , do đó 3
Sm1
=
−
. Trường hợp này hệ (VI) có nghiệm ( S ; P ) thoả
mãn khi và chỉ khi :
2
S4P≥
2
312
()
m1 m(m1)
≥
−−
2
4( m 1)
3 3m4(m1) m4
m( m 1)
−
⇔≥ ⇔ ≥ − ⇔ ≤
−
0m16(m1)⇔< ≤ ≠
Tóm lại các giá trị của m để hệ (V) có nghiệm x
≠
0 , y
≠
0 là : 0m16,m1
<
≤≠
Do đó :
(
]
{
}
5
T0;16\1=
Vậy : maxA = 16 ( chú ý không tồn tại minA )
Bài toán 6 : ( HSG quốc gia - Bảng A + B năm 2005 )
Cho hai số thực x, y thoả mãn : x3x13y2y
−
+= +−
Hãy tìm giá trị lớn nhất và nhỏ nhất của biểu thức Kxy
=
+
Lời giải : ĐKXĐ :
x1,y≥− ≥−2
Gọi T6 là tập giá trị của K . Ta có hệ sau có nghiệm:
6
mT∈⇔
3( x 1 y 2 ) m
x3x13y2y (VII)
xym xym
⎧
⎧++ + =
−+=+−
⎪⎪
⇔
⎨⎨
+= +=
⎪⎪
⎩⎩
Đặt ux=+1
và vy=+2
thì và hệ (VII) trở thành :
u,v 0≥
22 2
m
uv
3(u v) m 3
uvm3 1m
uv ( m 3)
29
⎧+=
⎪
+=
⎧⎪
⇔
⎨⎨
+=+
⎩⎪=−−
⎪
⎩
⇔
u , v là hai nghiệm của phương trình :
2
22
m1m
t t ( m 3) 0 18t 6mt m 9m 27 0
329
−+ −−=⇔ − +−−=
2
2
(10)
Từ đó , hệ (VII) có nghiệm ( x ; y ) sao cho khi và chỉ khi (10) có hai nghiệm không âm
và điều kiện là :
x1,y≥− ≥−
2
t
t
2
t
9(m 18m 54) 0
m9321
S0 m93
32
m9m27
P0
18
⎧
⎪′
Δ=− − − ≥
⎪+
⎪=≥ ⇔ ≤≤+
⎨
⎪
⎪−−
=≥
⎪
⎩
15
. Do đó 6
9321
T;9
2315
⎡
⎤
+
=+
⎢
⎥
⎣
⎦
Vậy : minK = 9321
2
+ , maxK = 9315+
Bình luận : Ưu thế của phương pháp trên là quy bài toán tìm GTLN , GTNN về bài toán tìm tham số
để hệ có nghiệm , vì vậy không cần chỉ rõ giá trị của biến số để biểu thức đạt GTLN , GTNN . Nếu
dùng các bất đẳng thức để đánh giá thì nhất thiết phải chỉ rõ các giá trị của biến số để tại đó biểu thức
đạt GTLN , GTNN .
Các bạn có thể mở rộng phương pháp này cho biểu thức có nhiều hơn hai biến số .
Cuối cùng mời các bạn vận dụng phương pháp trên để làm các bài tập sau :
Bài 1 : Cho hai số thực x , y thoả mãn : 22
2( ) 7xy xy
+
=++ .
Tìm giá trị lớn nhất , nhỏ nhất của biểu thức
=
−+ −
33
(2) (2Pxx yy)
Bài 2 : Cho hai số thực x , y thoả mãn :
+
++≤(1)(1)xx yy 0
.