§Ò 1.
Thêi gian 90 phót, Kh«ng ®−îc sö dông tμi liÖu,
1. H·y sö dông hμm r¨ng l−îc (cßn gäi lμ hμm trÝch mÉu) ®Ó m« t¶ qu¸ tr×nh trÝch mÉu
tÝn hiÖu còng nh− hai sai sè c¬ b¶n gi÷a ¶nh Fourier liªn tôc vμ kh«ng liªn tôc. Tõ ®ã,
h·y tr×nh bμy ý nghÜa øng dông ®Ó gi¶m thiÓu c¸c sai sè trong qu¸ tr×nh tÝnh c¸c gi¸
trÞ hμm mËt ®é phæ Su(jnΩ), n=0,1, … ,N cña tÝn hiÖu u(t) tõ c¸c gi¸ trÞ u0,u1,
… ,uN cña nã, trong ®ã uk= u(kTa) vμ Ta lμ chu kú lÊy mÉu.
2. Cho ®èi t−îng bÊt ®Þnh kh«ng chøa thμnh phÇn dao ®éng víi hμm truyÒn ®¹t:
S(s) = )( 2
210 sasaas
k
++ , a0,a1,a2,k lμ nh÷ng tham sè ch−a biÕt phô thuéc t .
Ng−êi ta ®· ®iÒu khiÓn ®èi t−îng nμy b»ng bé PID tù chØnh gi¸n tiÕp vμ mét bé tiÒn
xö lý M(s) ®Ó lμm gi¶m ®é qu¸ ®iÒu chØnh hÖ kÝn.
a) H·y x©y dùng c¬ cÊu nhËn d¹ng cho bé ®iÒu khiÓn thÝch nghi (d−íi d¹ng thuËt
to¸n). Nªu râ cÇn trÝch Ýt nhÊt bao nhiªu mÉu tÝn hiÖu th× ®ñ ®Ó cã thÓ x¸c ®Þnh
®−îc c¸c tham sè a0,a1,a2,k cña ®èi t−îng.
b) H·y x©y dùng c¬ cÊu chØnh ®Þnh c¸c tham sè cho hai bé ®iÒu khiÓn trªn.
c) CÇn cã gi¶ thiÕt g× vÒ tèc ®é thay ®æi c¸c tham sè a0,a1,a2,k (nhanh/chËm nh−
thÕ nμo) ®Ó hÖ thèng thÝch nghi trªn lμm viÖc cã hiÖu qu¶)?.
Gîi ý: NÕu ®· cã:
S(s) = )1)(1( 21 sTsTTs
k
++
th× M(s) = sT2
41
1
+ vμ bé ®iÒu khiÓn PID: )
1
1( sT
sT
kD
I
p++ tèi −u ®èi xøng sÏ cã:
TI = T1+4T2 , TD =
21
21
4
4
TT
TT
+, kp =2
2
21
8
)4(
kT
TTT +
3. H·y x©y dùng c¬ cÊu chØnh ®Þnh tham sè cho bé ®iÒu khiÓn ph¶n håi tÝn hiÖu ra y:
u
= p1w−p2y
®Ó ®iÒu khiÓn ®èi t−îng bÊt ®Þnh (tÝn hiÖu vμo lμ u vμ tÝn hiÖu ra lμ y):
S(s) = Tss
k
+
2, k, T lμ hai h»ng sè ch−a biÕt.
sao cho hÖ kÝn b¸m ®−îc theo m« h×nh mÉu:
G(s) = s31
1
+,
X¸c nhËn cña Bé m«n §KT§:
§Ò 2.
Thêi gian 90 phót. Kh«ng ®−îc sö dông tμi liÖu,
1. T¹i sao ph−¬ng ph¸p t×m nghiÖm ph−¬ng tr×nh Yule−Walker ®Ó x¸c ®Þnh tham sè m«
h×nh AR cña ®èi t−îng kh«ng liªn tôc khi ®èi t−îng cã tÝn hiÖu ®Çu vμo lμ ån tr¾ng l¹i
®−îc gäi ph−¬ng ph¸p nhËn d¹ng (chØ ra sai lÖch nμo ®−îc sö dông vμ nghiÖm cña
Yule−Walker sÏ lμm cho sai lÖch ®ã cã gi¸ trÞ nhá nhÊt). Tõ ®ã, h·y nªu ý nghÜa cña
ph−¬ng tr×nh Yule−Walker ®èi víi viÖc nhËn d¹ng chñ ®éng tham sè m« h×nh ARMA
nãi chung.
2. Cho ®èi t−îng bÊt ®Þnh kh«ng chøa thμnh phÇn dao ®éng víi hμm truyÒn ®¹t:
S(s) = 3
3
2
21
1sasasa
k
+++ , a1,a2,a3,k lμ c¸c tham sè ch−a biÕt phô thuéc t .
Ng−êi ta ®· ®iÒu khiÓn ®èi t−îng nμy b»ng bé PID tù chØnh gi¸n tiÕp.
a) H·y x©y dùng c¬ cÊu nhËn d¹ng cho bé ®iÒu khiÓn thÝch nghi (d−íi d¹ng thuËt
to¸n). Nªu râ cÇn trÝch Ýt nhÊt bao nhiªu mÉu tÝn hiÖu th× ®ñ ®Ó cã thÓ x¸c ®Þnh
®−îc c¸c tham sè a1,a2,a3,k cña ®èi t−îng.
b) H·y x©y dùng c¬ cÊu chØnh ®Þnh c¸c tham sè bé ®iÒu khiÓn PID.
c) CÇn cã gi¶ thiÕt g× vÒ tèc ®é thay ®æi c¸c tham sè a1,a2,a3,k (nhanh/chËm nh−
thÕ nμo) ®Ó hÖ thèng thÝch nghi trªn lμm viÖc cã hiÖu qu¶)?.
Gîi ý: NÕu ®· cã:
S(s) = )1)(1)(1( 321 sTsTsT
k
+++
th× bé ®iÒu khiÓn PID: )
1
1( sT
sT
kD
I
p++ tèi −u ®é lín sÏ lμ:
TI = T1+T2 , TD =
21
21
TT
TT
+, kp =
3
21
2kT
TT +
3. H·y x©y dùng c¬ cÊu chØnh ®Þnh tham sè cho bé ®iÒu khiÓn ph¶n håi tÝn hiÖu ra y:
u
= p1w+p2y
®Ó ®iÒu khiÓn ®èi t−îng bÊt ®Þnh (tÝn hiÖu vμo lμ u vμ tÝn hiÖu ra lμ y):
S(s) = Tss
k
+
2, k, T lμ hai h»ng sè ch−a biÕt.
sao cho hÖ kÝn b¸m ®−îc theo m« h×nh mÉu:
G(s) = s51
1
+,
X¸c nhËn cña Bé m«n §KT§:
CuuDuongThanCong.com https://fb.com/tailieudientucntt
§Ò 1.
Thêi gian 90 phót, §−îc sö dông tμi liÖu,
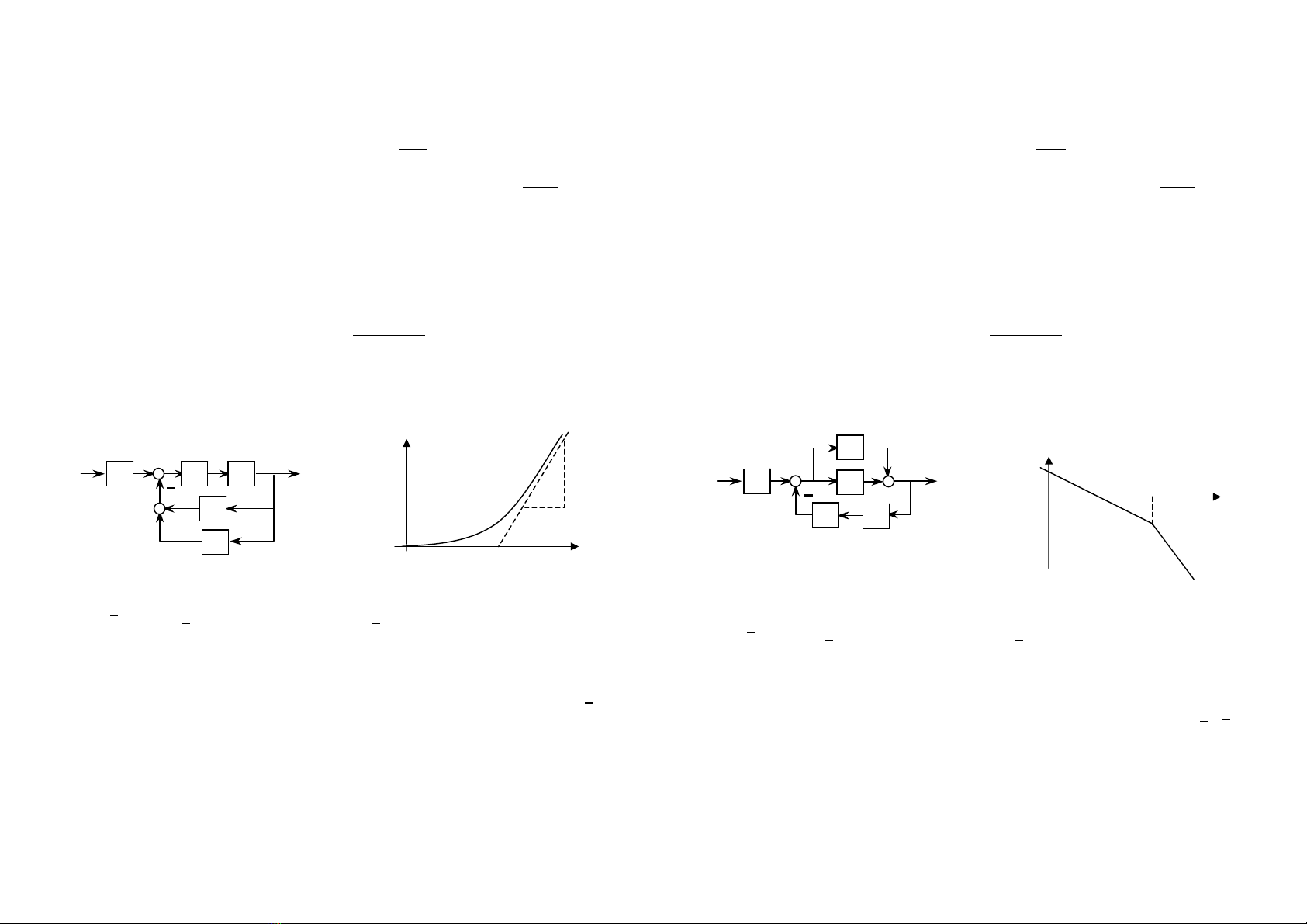
Bμi 1: Cho hÖ kÝn m« t¶ ë h×nh 1.
1. (1 ®iÓm) H·y x¸c ®Þnh hμm truyÒn ®¹t t−¬ng ®−¬ng G(s) cña hÖ.
2. (2 ®iÓm) BiÕt r»ng G1=G2=G3=G4=1 vμ G5=1
1
+s. H·y tÝnh hμm träng l−îng
g(t) vμ hμm qu¸ ®é h(t) cña hÖ. Tõ ®ã kiÓm tra l¹i quan hÖ g(t)= dt
tdh )( .
3. (2 ®iÓm) BiÕt r»ng G1=G3=G4+G5=1 vμ G2 lμ kh©u tÝch ph©n−qu¸n tÝnh bËc
nhÊt cã hμm qu¸ ®é h2(t) cho ë h×nh 2. H·y x¸c ®Þnh k ®Ó hÖ kÝn lμ mét kh©u dao
®éng bËc 2 t¾t dÇn. Tõ ®ã tÝnh cô thÓ ®é qu¸ ®iÒu chØnh Δhmax vμ thêi gian qu¸ ®é
T5% øng víi k=2.
4. (1 ®iÓm) G1=k, G3=G4+G5=1 vμ G2=
12
1
(1 )Ts Ts+. T×m ®iÒu kiÖn cho T1, T2 ®Ó
hÖ kÝn cã d¹ng dao ®éng bËc hai. Chøng minh r»ng thêi gian qu¸ ®é T5% cña hÖ
kh«ng phô thuéc h»ng sè k.
Bμi 2: Cho ®èi t−îng cã m« h×nh tr¹ng th¸i.
dt
xd =01
40
⎛⎞
⎜⎟
⎝⎠
x+⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
1
0u, y=x2, trong ®ã x=⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
2
1
x
x.
1. (1 ®iÓm) H·y thiÕt kÕ bé ®iÒu khiÓn ph¶n håi tr¹ng th¸i sao cho víi nã, hÖ thèng
cã hai ®iÓm cùc míi lμ s1= s2= −2.
2. (1 ®iÓm) H·y x¸c ®Þnh bé quan s¸t tr¹ng th¸i Luenberger ®Ó tÝnh xÊp xØ x
~≈x
tr¹ng th¸i cña ®èi t−îng víi hai ®iÓm cùc cho tr−íc lμ
λ
1= −4 vμ
λ
2= −5.
3. (1,5 ®iÓm) VÏ s¬ ®å khèi m« t¶ hÖ kÝn bao gåm ®èi t−îng ®· cho, bé ®iÒu khiÓn
ph¶n håi tr¹ng th¸i t×m ®−îc ë c©u 1 vμ bé quan s¸t tr¹ng th¸i Luenberger ®· t×m
®−îc ë c©u 2. ViÕt ph−¬ng tr×nh tr¹ng th¸i vμ ®a thøc ®Æc tÝnh cho hÖ kÝn ®ã.
4. (0,5 ®iÓm) Cã thÓ cã bao nhiªu bé ®iÒu khiÓn ph¶n håi tr¹ng th¸i tháa m·n yªu
cÇu nªu trong c©u 1?.
§Ò 2.
Thêi gian 90 phót, §−îc sö dông tμi liÖu,
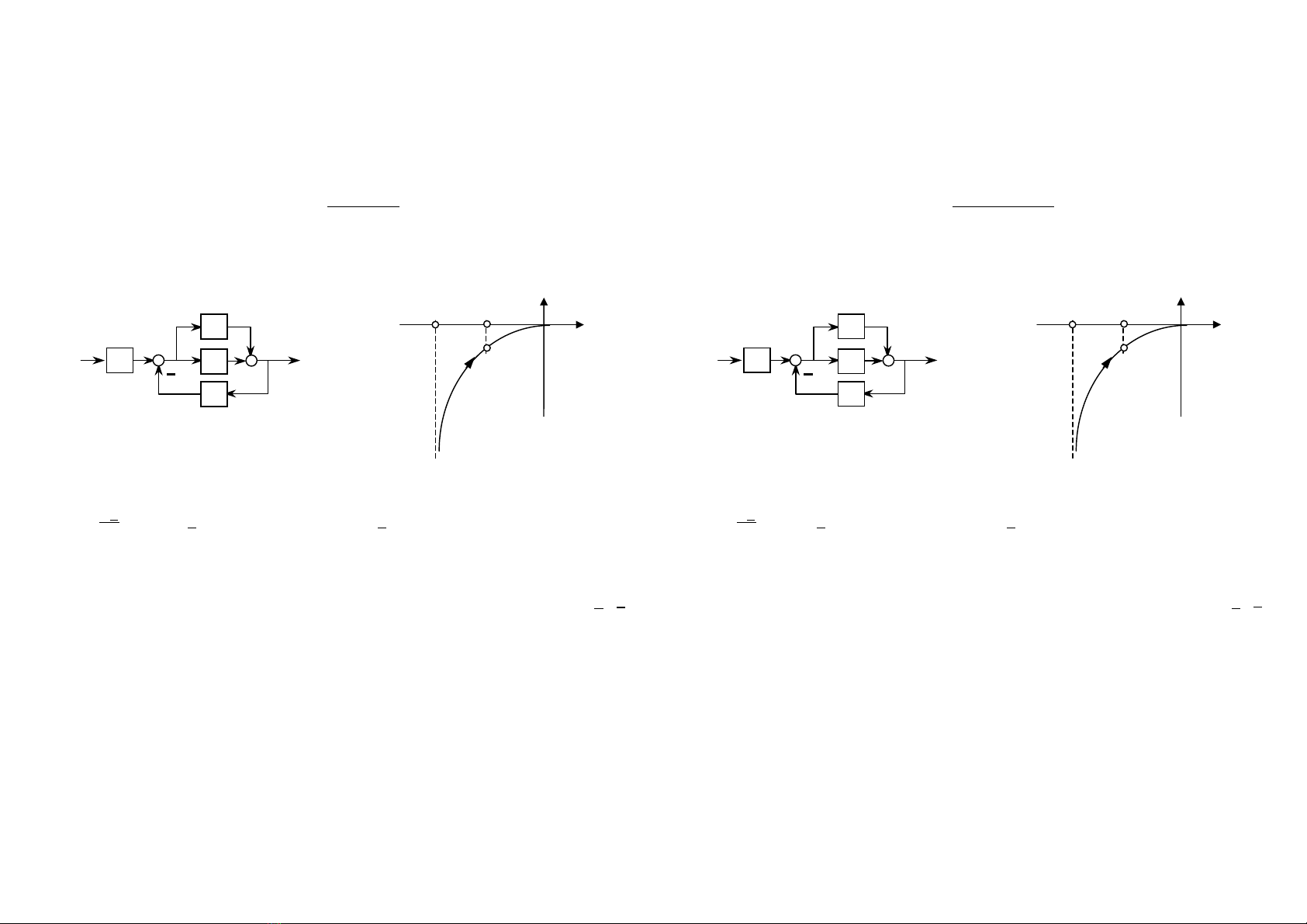
Bμi 1: Cho hÖ kÝn m« t¶ ë h×nh 1.
1. (1 ®iÓm) H·y x¸c ®Þnh hμm truyÒn ®¹t t−¬ng ®−¬ng G(s) cña hÖ.
2. (2 ®iÓm) BiÕt r»ng G1=G2=G3=G4=1 vμ G5=2
1
+s. H·y tÝnh hμm träng l−îng
g(t) vμ hμm qu¸ ®é h(t) cña hÖ. Tõ ®ã kiÓm tra l¹i quan hÖ g(t)= dt
tdh )( .
3. (2 ®iÓm) BiÕt r»ng G1=G3=G4+G5=1 vμ G2 lμ kh©u tÝch ph©n−qu¸n tÝnh bËc
nhÊt cã ®−êng ®å thÞ Bode L2(
ω
) cho ë h×nh 2. H·y x¸c ®Þnh T ®Ó hÖ kÝn lμ mét
kh©u dao ®éng bËc 2 t¾t dÇn. Tõ ®ã tÝnh cô thÓ ®é qu¸ ®iÒu chØnh Δhmax vμ thêi
gian qu¸ ®é T5% øng víi T=0,1.
5. (1 ®iÓm) G1=k, G2=G3=1 vμ G4+G5=
12
1
(1 )Ts Ts+. T×m ®iÒu kiÖn cho T1, T2 ®Ó
hÖ kÝn cã d¹ng dao ®éng bËc hai. Chøng minh r»ng thêi gian qu¸ ®é T5% cña hÖ
kh«ng phô thuéc h»ng sè k.
Bμi 2: Cho ®èi t−îng cã m« h×nh tr¹ng th¸i.
dt
xd =12
01
⎛⎞
⎜⎟
−
⎝⎠
x+⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
1
0u, y=x2, trong ®ã x=⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
2
1
x
x.
1. (1 ®iÓm) H·y thiÕt kÕ bé ®iÒu khiÓn ph¶n håi tr¹ng th¸i sao cho víi nã, hÖ thèng
cã hai ®iÓm cùc míi lμ s1= −2, s2= −4.
2. (1 ®iÓm) H·y x¸c ®Þnh bé quan s¸t tr¹ng th¸i Luenberger ®Ó tÝnh xÊp xØ x
~≈x
tr¹ng th¸i cña ®èi t−îng víi hai ®iÓm cùc cho tr−íc lμ
λ
1=
λ
2= −5.
3. (1,5 ®iÓm) VÏ s¬ ®å khèi m« t¶ hÖ kÝn bao gåm ®èi t−îng ®· cho, bé ®iÒu khiÓn
ph¶n håi tr¹ng th¸i t×m ®−îc ë c©u 1 vμ bé quan s¸t tr¹ng th¸i Luenberger ®· t×m
®−îc ë c©u 2. ViÕt ph−¬ng tr×nh tr¹ng th¸i vμ ®a thøc ®Æc tÝnh cho hÖ kÝn ®ã.
4. (0,5 ®iÓm) Cã thÓ cã bao nhiªu bé ®iÒu khiÓn ph¶n håi tr¹ng th¸i tháa m·n yªu
cÇu nªu trong c©u 1?.
H×nh 1
u
y
G1 G2G3
G4
G5
h2(t)
t
H×nh 2
2
k
1 H×nh 1
u
y
G1
G2G3
G4
G5
L
2(
ω
)
ω
H×nh 2
4
T−1
−
20dB/dec
−40dB/dec
CuuDuongThanCong.com https://fb.com/tailieudientucntt
§Ò thi l¹i (§Ò 1)
Thêi gian 90 phót, §−îc sö dông tμi liÖu,
Bμi 1: Cho hÖ kÝn m« t¶ ë h×nh 1.
1. (1 ®iÓm) H·y x¸c ®Þnh hμm truyÒn ®¹t t−¬ng ®−¬ng G(s) cña hÖ.
2. (2 ®iÓm) BiÕt r»ng G1=G4=1 vμ G2+G3 lμ kh©u tÝch ph©n−qu¸n tÝnh bËc nhÊt
cã ®−êng ®å thÞ ®Æc tÝnh tÇn biªn−pha cho ë h×nh 2. H·y tÝnh hμm träng l−îng
g(t) vμ hμm qu¸ ®é h(t) cña hÖ.
3. (2 ®iÓm) G1=k, G4=1 vμ G2+G3=
12
1
(1 )Ts Ts+. T×m ®iÒu kiÖn cho T1, T2 ®Ó hÖ
kÝn cã d¹ng dao ®éng bËc hai. Chøng minh r»ng thêi gian qu¸ ®é T5% cña hÖ
kh«ng phô thuéc h»ng sè k.
Bμi 2: Cho ®èi t−îng cã m« h×nh tr¹ng th¸i.
dt
xd =02
13
⎛⎞
⎜⎟
−
⎝⎠
x+1
2
⎛⎞
⎜⎟
⎝⎠
u, y=x2, trong ®ã x=⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
2
1
x
x.
1. (1 ®iÓm) H·y thiÕt kÕ bé ®iÒu khiÓn ph¶n håi tr¹ng th¸i sao cho víi nã, hÖ thèng
cã hai ®iÓm cùc míi lμ s1 = −2+5j, s2 = −2−5j.
2. (1 ®iÓm) H·y x¸c ®Þnh bé quan s¸t tr¹ng th¸i Luenberger ®Ó tÝnh xÊp xØ x
~≈x
tr¹ng th¸i cña ®èi t−îng víi hai ®iÓm cùc cho tr−íc lμ
λ
1=
λ
2= −5.
3. (1,5 ®iÓm) VÏ s¬ ®å khèi m« t¶ hÖ kÝn bao gåm ®èi t−îng ®· cho, bé ®iÒu khiÓn
ph¶n håi tr¹ng th¸i t×m ®−îc ë c©u 1 vμ bé quan s¸t tr¹ng th¸i Luenberger ®· t×m
®−îc ë c©u 2. ViÕt ph−¬ng tr×nh tr¹ng th¸i vμ ®a thøc ®Æc tÝnh cho hÖ kÝn ®ã.
4. (0,5 ®iÓm) Cã thÓ cã bao nhiªu bé ®iÒu khiÓn ph¶n håi tr¹ng th¸i tháa m·n yªu
cÇu nªu trong c©u 1?.
§Ò thi l¹i (§Ò 2)
Thêi gian 90 phót, §−îc sö dông tμi liÖu,
Bμi 1: Cho hÖ kÝn m« t¶ ë h×nh 1.
1. (1 ®iÓm) H·y x¸c ®Þnh hμm truyÒn ®¹t t−¬ng ®−¬ng G(s) cña hÖ.
2. (2 ®iÓm) BiÕt r»ng G1=G4=1 vμ G2+G3 lμ kh©u tÝch ph©n−qu¸n tÝnh bËc nhÊt
cã ®−êng ®å thÞ ®Æc tÝnh tÇn biªn−pha cho ë h×nh 2. H·y tÝnh hμm träng l−îng
g(t) vμ hμm qu¸ ®é h(t) cña hÖ.
3. (2 ®iÓm) G1= G4=1 vμ G2+G3=
12
(1 )(1 )
k
Ts Ts++
. T×m ®iÒu kiÖn cho k, T1, T2
®Ó hÖ kÝn cã d¹ng dao ®éng bËc hai. X¸c ®Þnh thêi gian qu¸ ®é T5% cña hÖ vμ sai
lÖch tÜnh khi tÝn hiÖu vμo lμ 1(t).
Bμi 2: Cho ®èi t−îng cã m« h×nh tr¹ng th¸i.
dt
xd =02
11
⎛⎞
⎜⎟
⎝⎠
x+1
2
⎛⎞
⎜⎟
⎝⎠
u, y=x2, trong ®ã x=⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
2
1
x
x.
1. (1 ®iÓm) H·y thiÕt kÕ bé ®iÒu khiÓn ph¶n håi tr¹ng th¸i sao cho víi nã, hÖ thèng
cã hai ®iÓm cùc míi lμ s1 = −3+2j, s2 = −3−2j.
2. (1 ®iÓm) H·y x¸c ®Þnh bé quan s¸t tr¹ng th¸i Luenberger ®Ó tÝnh xÊp xØ x
~≈x
tr¹ng th¸i cña ®èi t−îng víi hai ®iÓm cùc cho tr−íc lμ
λ
1=
λ
2= −4.
3. (1,5 ®iÓm) VÏ s¬ ®å khèi m« t¶ hÖ kÝn bao gåm ®èi t−îng ®· cho, bé ®iÒu khiÓn
ph¶n håi tr¹ng th¸i t×m ®−îc ë c©u 1 vμ bé quan s¸t tr¹ng th¸i Luenberger ®· t×m
®−îc ë c©u 2. ViÕt ph−¬ng tr×nh tr¹ng th¸i vμ ®a thøc ®Æc tÝnh cho hÖ kÝn ®ã.
4. (0,5 ®iÓm) Cã thÓ cã bao nhiªu bé ®iÒu khiÓn ph¶n håi tr¹ng th¸i tháa m·n yªu
cÇu nªu trong c©u 1?.
H×nh 1
u
y
G1
G4
G3
G2
ImG
H×nh 2
2 ReG1
ω
=1
ω
=0
ω
=
∞
H×nh 1
u
y
G1
G4
G3
G2
ImG
H×nh 2
4 ReG 2
ω
=1
ω
=0
ω
=∞
CuuDuongThanCong.com https://fb.com/tailieudientucntt
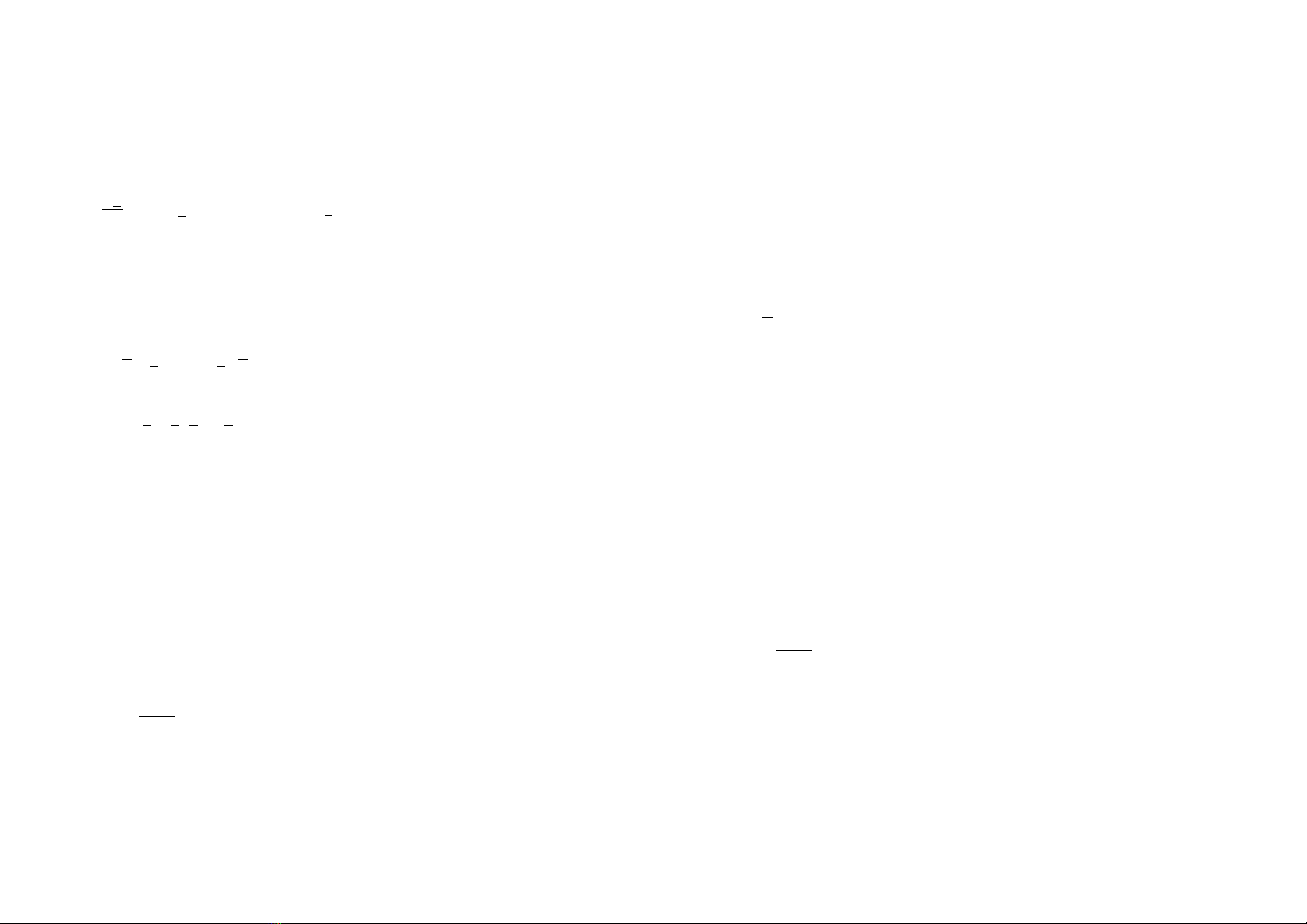
§Ò 1.
Thêi gian 90 phót
§−îc sö dông tμi liÖu,
1. a) (1 ®iÓm) §Ó cã thÓ ¸p dông ®−îc ph−¬ng ph¸p biÕn ph©n th× bμi to¸n tèi −u cÇn
ph¶i tháa m·n nh÷ng ®iÒu kiÖn nμo?.
b) (3 ®iÓm) Cho ®èi t−îng víi mét tÝn hiÖu vμo u m« t¶ bëi
dt
xd =ux ⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
1
0
01
20 , trong ®ã x = ⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
2
1
x
x lμ vector biÕn tr¹ng th¸i.
H·y x¸c ®Þnh bé ®iÒu khiÓn ph¶n håi tr¹ng th¸i hoμn toμn ®Ó æn ®Þnh ®èi t−îng
theo quan ®iÓm tèi −u n¨ng l−îng, tøc lμ víi bé ®iÒu khiÓn ®ã, khi cã mét nhiÔu
t¸c ®éng tøc thêi ®¸nh bËt hÖ ra khái ®iÓm c©n b»ng 0 th× sau ®ã hÖ cã kh¶ n¨ng
tù quay vÒ ®iÓm c©n b»ng 0 vμ n¨ng l−îng cÇn thiÕt cho qu¸ tr×nh tù quay vÒ tÝnh
theo
Q=∫
∞
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
0
2
2
1
106
24
2
1dtuxxT
lμ nhá nhÊt.
(Gîi ý: xTEx=xTETx)
2. (2 ®iÓm) Cho bμi to¸n tèi −u tÜnh
Q = 2121
2
2
2
121082 uuuuuu +−−+ → min
a) H·y t×m nghiÖm bμi to¸n theo ph−¬ng ph¸p Newton/Raphson víi 2 b−íc tÝnh kÓ tõ
®iÓm xuÊt ph¸t tïy ý ®−îc chän tr−íc.
b) Cã nhËn xÐt g× vÒ nghiÖm t×m ®−îc.
3. §Ó ®iÒu khiÓn ®èi t−îng bÊt ®Þnh (tÝn hiÖu vμo lμ u vμ tÝn hiÖu ra lμ y):
S(s) = Ts
k
+3, k, T lμ hai h»ng sè ch−a biÕt.
ng−êi ta sö dông bé ®iÒu khiÓn:
u
= p1w−p2y
a) (3 ®iÓm) H·y x©y dùng c¬ cÊu chØnh ®Þnh sao cho hÖ kÝn b¸m ®−îc theo m« h×nh
mÉu (biÖn luËn ®Ó bμi to¸n cã nghiÖm):
G(s) = s41
1
+,
b) (1 ®iÓm) Cã thÓ xem c¬ cÊu chØnh ®Þnh t×m ®−îc chÝnh lμ kh©u nhËn d¹ng tham sè
m« h×nh ®èi t−îng ®−îc kh«ng vμ t¹i sao?
§Ò 2.
Thêi gian 90 phót
§−îc sö dông tμi liÖu,
1. a) (1 ®iÓm) §Ó cã thÓ ¸p dông ®−îc ph−¬ng ph¸p quy ho¹ch ®éng cña Bellman th× bμi
to¸n tèi −u cÇn ph¶i tháa m·n nh÷ng ®iÒu kiÖn nμo?.
b) (3 ®iÓm) Cho hÖ m« t¶ bëi
xk+1= axk+buk, k=0,1,2,3
trong ®ã a,b lμ hai h»ng sè cho tr−íc. H·y x¸c ®Þnh d·y tÝn hiÖu ®iÒu khiÓn
u0,u1,u2,u3 ®Ó ®−a hÖ tõ mét ®iÓm tr¹ng ®Çu x0 tïy ý, nh−ng cho tr−íc tíi ®−îc
®iÓm tr¹ng th¸i x4 bÊt kú vμ chi phÝ cho qu¸ tr×nh chuyÓn ®æi tr¹ng th¸i ®ã tÝnh
theo
Q=∑
=
+
3
0
22 )(
2
1
kkk ux
lμ nhá nhÊt.
2. (2 ®iÓm) Cho bμi to¸n tèi −u tÜnh
Q = 2121
2
2
2
11452 uuuuuu +−−+ → min
a) H·y t×m nghiÖm bμi to¸n theo ph−¬ng ph¸p Newton/Raphson víi 2 b−íc tÝnh kÓ tõ
®iÓm xuÊt ph¸t tïy ý ®−îc chän tr−íc.
b) Cã nhËn xÐt g× vÒ nghiÖm t×m ®−îc.
3. §Ó ®iÒu khiÓn ®èi t−îng bÊt ®Þnh (tÝn hiÖu vμo lμ u vμ tÝn hiÖu ra lμ y):
S(s) = Ts
k
+2, k, T lμ hai h»ng sè ch−a biÕt.
ng−êi ta sö dông bé ®iÒu khiÓn:
u
= p1w−p2y
a) (3 ®iÓm) H·y x©y dùng c¬ cÊu chØnh ®Þnh sao cho hÖ kÝn b¸m ®−îc theo m« h×nh
mÉu (biÖn luËn ®Ó bμi to¸n cã nghiÖm):
G(s) = s61
1
+,
b) (1 ®iÓm) Cã thÓ xem c¬ cÊu chØnh ®Þnh t×m ®−îc chÝnh lμ kh©u nhËn d¹ng tham sè
m« h×nh ®èi t−îng ®−îc kh«ng vμ t¹i sao?
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Thêi gian 90 phót
§−îc sö dông tμi liÖu,
1. Cho bμi to¸n tèi −u tÜnh
Q = 22
121 212
2514uuu uuu+−− + → min víi u=(u1,u2)T
a) (1,5 ®iÓm) H·y x¸c ®Þnh u2 theo ph−¬ng ph¸p Newton/Raphson víi 2 b−íc tÝnh kÓ
tõ ®iÓm xuÊt ph¸t u0 tïy ý ®−îc chän tr−íc.
b) (1 ®iÓm) H·y chØ r»ng u2 t×m ®−îc ë b−íc a) lμ nghiÖm u* cña bμi to¸n ®· cho.
2. Cho ®èi t−îng víi mét tÝn hiÖu vμo u vμ hai biÕn tr¹ng th¸i m« t¶ bëi
dt
xd =⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
00
10 x + ⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
1
0u, trong ®ã x = ⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
2
1
x
x lμ vector biÕn tr¹ng th¸i.
a) (2,5 ®iÓm) H·y x¸c ®Þnh bé ®iÒu khiÓn ph¶n håi tr¹ng th¸i hoμn toμn ®Ó æn ®Þnh
®èi t−îng theo quan ®iÓm tèi −u n¨ng l−îng, tøc lμ víi bé ®iÒu khiÓn ®ã, khi cã
mét nhiÔu t¸c ®éng tøc thêi ®¸nh bËt hÖ ra khái ®iÓm c©n b»ng 0 th× sau ®ã hÖ cã
kh¶ n¨ng tù quay vÒ ®iÓm c©n b»ng 0 vμ n¨ng l−îng cÇn thiÕt cho qu¸ tr×nh tù
quay vÒ tÝnh theo
Q = ∫
∞++
0
22
2
2
1)(
2
1dtbuaxx , a, b > 0
lμ nhá nhÊt.
b) (0,5 ®iÓm) H·y chØ r»ng víi bé ®iÒu khiÓn t×m ®−îc, hÖ kÝn lμ æn ®Þnh.
c) (0,5 ®iÓm) H·y viÕt l¹i bé ®iÒu khiÓn ph¶n håi tr¹ng th¸i t×m ®−îc d−íi d¹ng ph¶n
håi tÝn hiÖu ra vμ tõ ®ã chØ r»ng b¶n th©n bé ®iÒu khiÓn ®ã lμ kh«ng æn ®Þnh.
3. Cho ®èi t−îng tuyÕn tÝnh
dt
xd =2
2
12 1122
x
xxuxdxd
⎛⎞
⎜⎟
⎜⎟
−++ +
⎝⎠
cã d1(t), d2(t) lμ hai tham sè bÊt ®Þnh phô thuéc thêi gian.
a) (2,5 ®iÓm) H·y x©y dùng bé ®iÒu khiÓn thÝch nghi ®Ó hÖ kÝn lu«n b¸m ®−îc theo
m« h×nh mÉu:
m
dx
dt =⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−− 11
10 xm + ⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
1
0w
b) (0,5 ®iÓm) Víi bé ®iÒu khiÓn t×m ®−îc, ng−êi ta cã thÓ x¸c ®Þnh ®−îc hai tham sè
bÊt ®Þnh d1(t), d2(t) cña ®èi t−îng ®−îc kh«ng vμ t¹i sao.
4. (1 ®iÓm) H·y chØ r»ng ®èi t−îng cã hμm truyÒn ®¹t S(s)= 21
s
s
kh«ng thÓ ®iÒu
khiÓn æn ®Þnh ®−îc theo nguyªn lý ph¶n håi ®Çu ra b»ng mét bé ®iÒu khiÓn æn ®Þnh.
Thêi gian 90 phót
§−îc sö dông tμi liÖu,
1. Cho bμi to¸n tèi −u tÜnh
Q = 22
121 212
2514uuu uuu+−− + → min víi u=(u1,u2)T
a) (1,5 ®iÓm) H·y x¸c ®Þnh u2 theo ph−¬ng ph¸p Newton/Raphson víi 2 b−íc tÝnh kÓ
tõ ®iÓm xuÊt ph¸t u0 tïy ý ®−îc chän tr−íc.
b) (1 ®iÓm) H·y chØ r»ng u2 t×m ®−îc ë b−íc a) lμ nghiÖm u* cña bμi to¸n ®· cho.
2. Cho ®èi t−îng víi mét tÝn hiÖu vμo u vμ hai biÕn tr¹ng th¸i m« t¶ bëi
dt
xd =⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
00
10 x + ⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
1
0u, trong ®ã x = ⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
2
1
x
x lμ vector biÕn tr¹ng th¸i.
a) (2,5 ®iÓm) H·y x¸c ®Þnh bé ®iÒu khiÓn ph¶n håi tr¹ng th¸i hoμn toμn ®Ó æn ®Þnh
®èi t−îng theo quan ®iÓm tèi −u n¨ng l−îng, tøc lμ víi bé ®iÒu khiÓn ®ã, khi cã
mét nhiÔu t¸c ®éng tøc thêi ®¸nh bËt hÖ ra khái ®iÓm c©n b»ng 0 th× sau ®ã hÖ cã
kh¶ n¨ng tù quay vÒ ®iÓm c©n b»ng 0 vμ n¨ng l−îng cÇn thiÕt cho qu¸ tr×nh tù
quay vÒ tÝnh theo
Q = ∫
∞++
0
22
2
2
1)(
2
1dtbuaxx , a, b > 0
lμ nhá nhÊt.
b) (0,5 ®iÓm) H·y chØ r»ng víi bé ®iÒu khiÓn t×m ®−îc, hÖ kÝn lμ æn ®Þnh.
c) (0,5 ®iÓm) H·y viÕt l¹i bé ®iÒu khiÓn ph¶n håi tr¹ng th¸i t×m ®−îc d−íi d¹ng ph¶n
håi tÝn hiÖu ra vμ tõ ®ã chØ r»ng b¶n th©n bé ®iÒu khiÓn ®ã lμ kh«ng æn ®Þnh.
3. Cho ®èi t−îng tuyÕn tÝnh
dt
xd =2
2
12 1122
x
xxuxdxd
⎛⎞
⎜⎟
⎜⎟
−++ +
⎝⎠
cã d1(t), d2(t) lμ hai tham sè bÊt ®Þnh phô thuéc thêi gian.
a) (2,5 ®iÓm) H·y x©y dùng bé ®iÒu khiÓn thÝch nghi ®Ó hÖ kÝn lu«n b¸m ®−îc theo
m« h×nh mÉu:
m
dx
dt =⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−− 11
10 xm + ⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
1
0w
b) (0,5 ®iÓm) Víi bé ®iÒu khiÓn t×m ®−îc, ng−êi ta cã thÓ x¸c ®Þnh ®−îc hai tham sè
bÊt ®Þnh d1(t), d2(t) cña ®èi t−îng ®−îc kh«ng vμ t¹i sao.
4. (1 ®iÓm) H·y chØ r»ng ®èi t−îng cã hμm truyÒn ®¹t S(s)= 21
s
s
kh«ng thÓ ®iÒu
khiÓn æn ®Þnh ®−îc theo nguyªn lý ph¶n håi ®Çu ra b»ng mét bé ®iÒu khiÓn æn ®Þnh.
CuuDuongThanCong.com https://fb.com/tailieudientucntt