Ch đ 1ủ ề
VÉC T TRONG KHÔNG GIANƠ
PH NG PHÁPƯƠ :
Đ bi u di n m t véc t qua các véc t ể ể ễ ộ ơ ơ
khác ,ch ng minh m t đ ng th c véc ứ ộ ẳ ứ
t ,ch ng minh hai véc t vuông góc hay ba ơ ứ ơ
véc t đ ng ph ng …,ta s d ng các quy ơ ồ ẳ ử ụ
t c :ba đi m,hình bình hành,trung ắ ể
tuy n,trung đi m,tr ng tâm tam giác,tr ng ế ể ọ ọ
tr ng t di n,đ ng chéo hình h p ọ ứ ệ ườ ộ
B
S
D
C
O
G
A
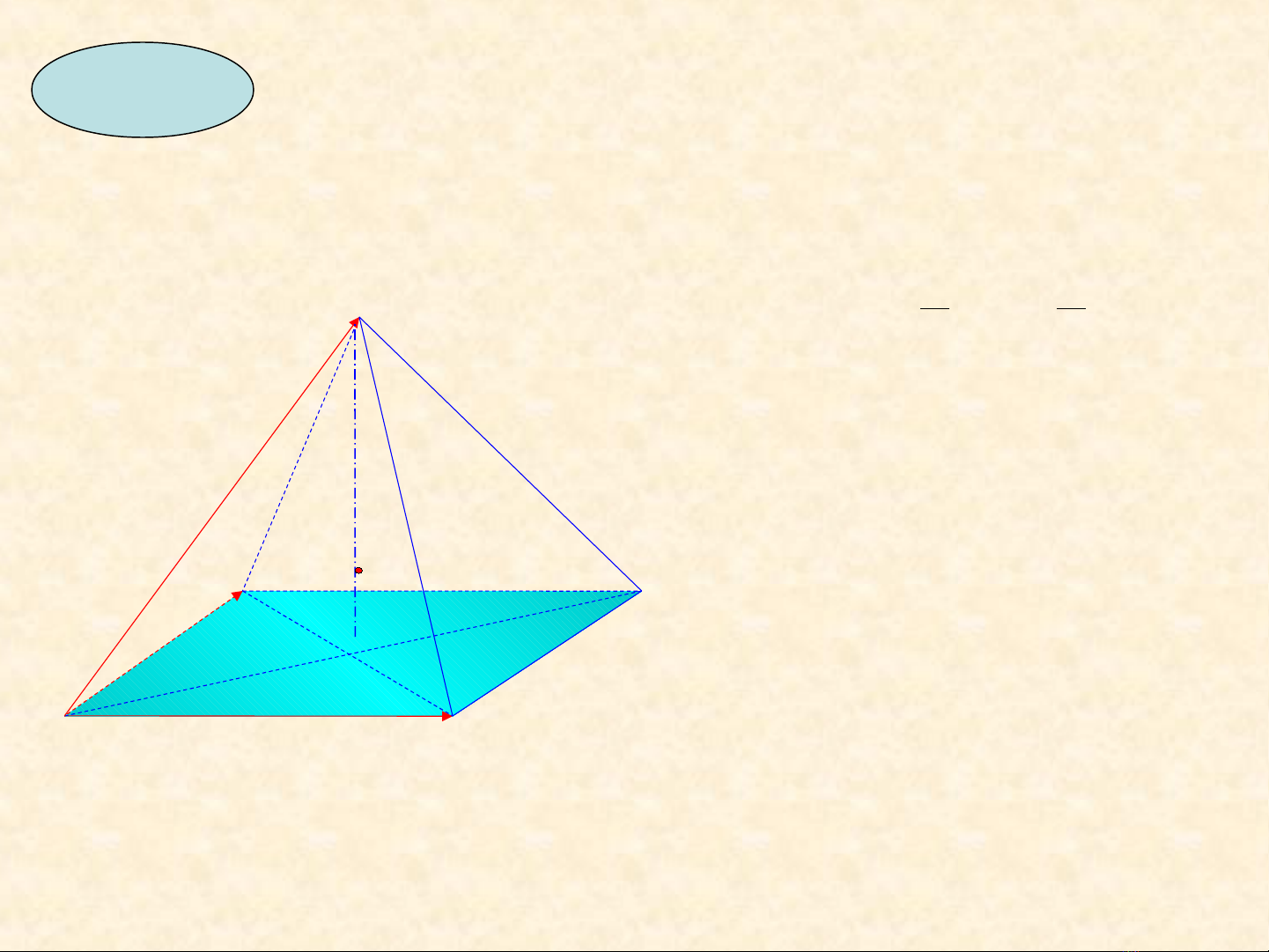
Ví d 1ụCho hình chóp S.ABCD có đáy là hình bình hành
tâm O.Ch ng minh r ng: 1)ứ ằ
( )
) 2
)2
3 1
)2 2
i AB AD AS SB SD
ii SO BA SC DB
iii SO DC AD SB SD
+ − = +
− − =
+ − = −
uuur uuur uuur uur uuur
uuur uuur uuur
uuur uuur uuur uur uuur
2) Tìm đi m G sao cho ể
GS GA GB GC GD O
+ + + + =
uuur uuur uuur uuur uuur ur
O
O
'
D'
A'
B'
C'
AB
C
D
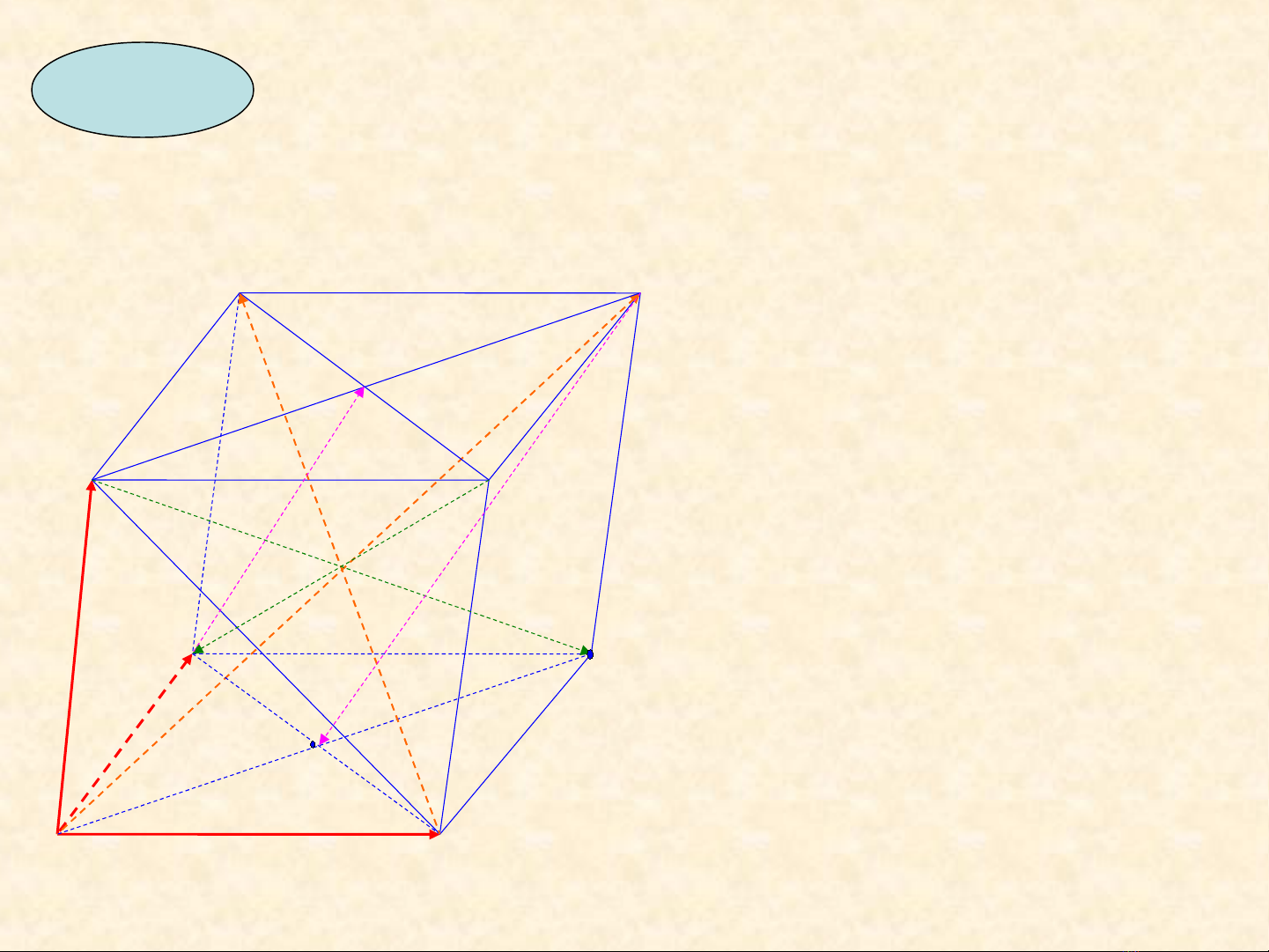
Ví d 2ụCho hình h p ộ
ABCD.A/B/C/D/ có tâm hai
đáy l n l t là O và O/.Các ầ ượ
véc t ơ
, ,AB a AD b AA c
′
= = =
uuur r uuur r uuur r
Hãy bi u di n các vec t ể ễ ơ
, , , ,BD A C B D DO C O
′ ′ ′ ′ ′
uuuur uuuur uuuur uuuur uuuur
theo
, ,a b c
r r r
A
B
C
D
M
G
I
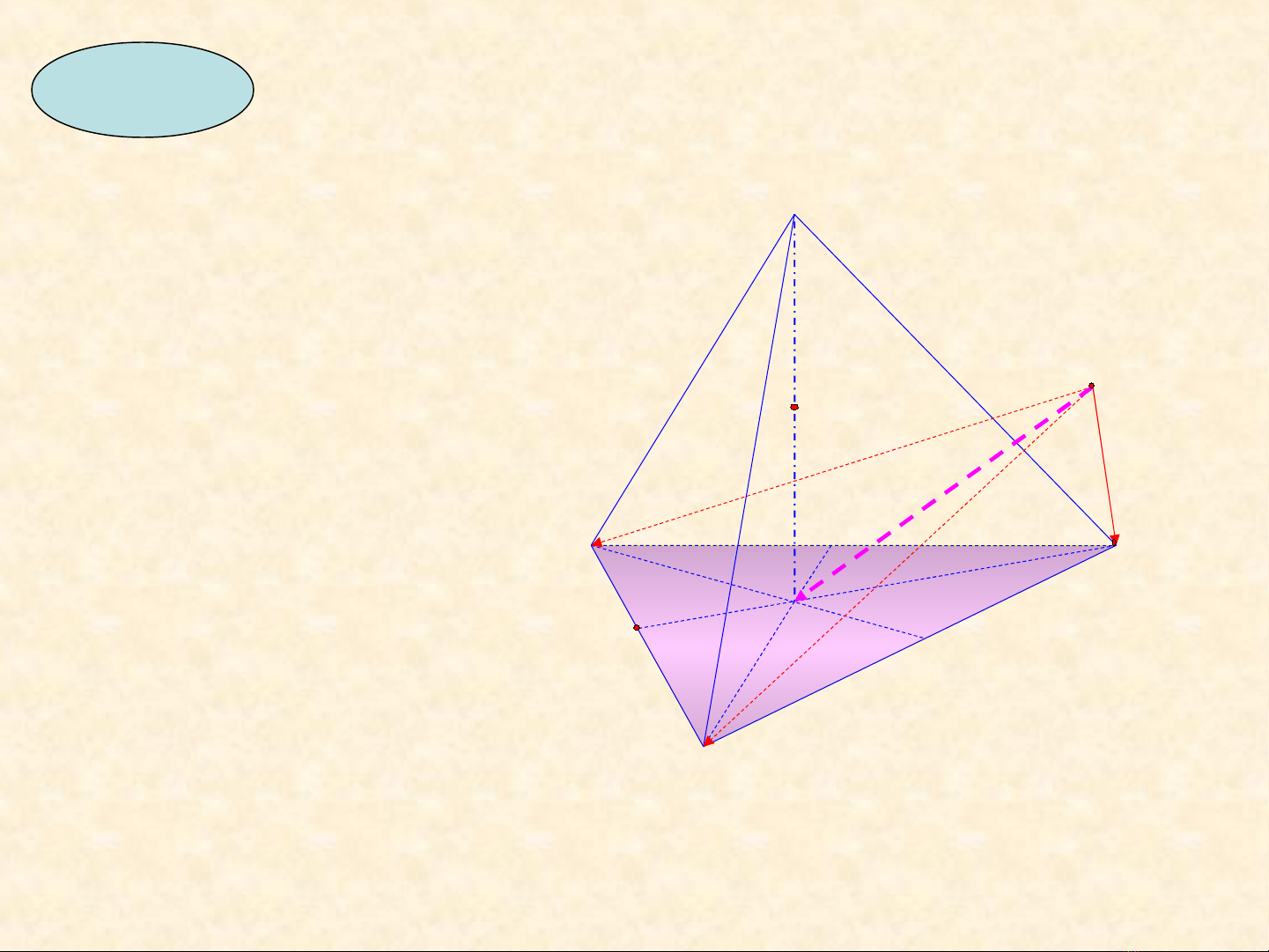
Ví d 3ụ
Cho t di n ABCD,G là ứ ệ
tr ng tâm tam giác BCD,I là ọ
trung đi m AG,M là đi m ể ể
b t kỳ.Ch ng minh r ngấ ứ ằ :
) 3
)3
a MB MC MD MG
b IA IB IC ID O
+ + =
+ + + =
uuur uuuur uuuur uuuur
uur uur uur uur ur
M
O'
O
D'
A' B'
C'
AB
C
D
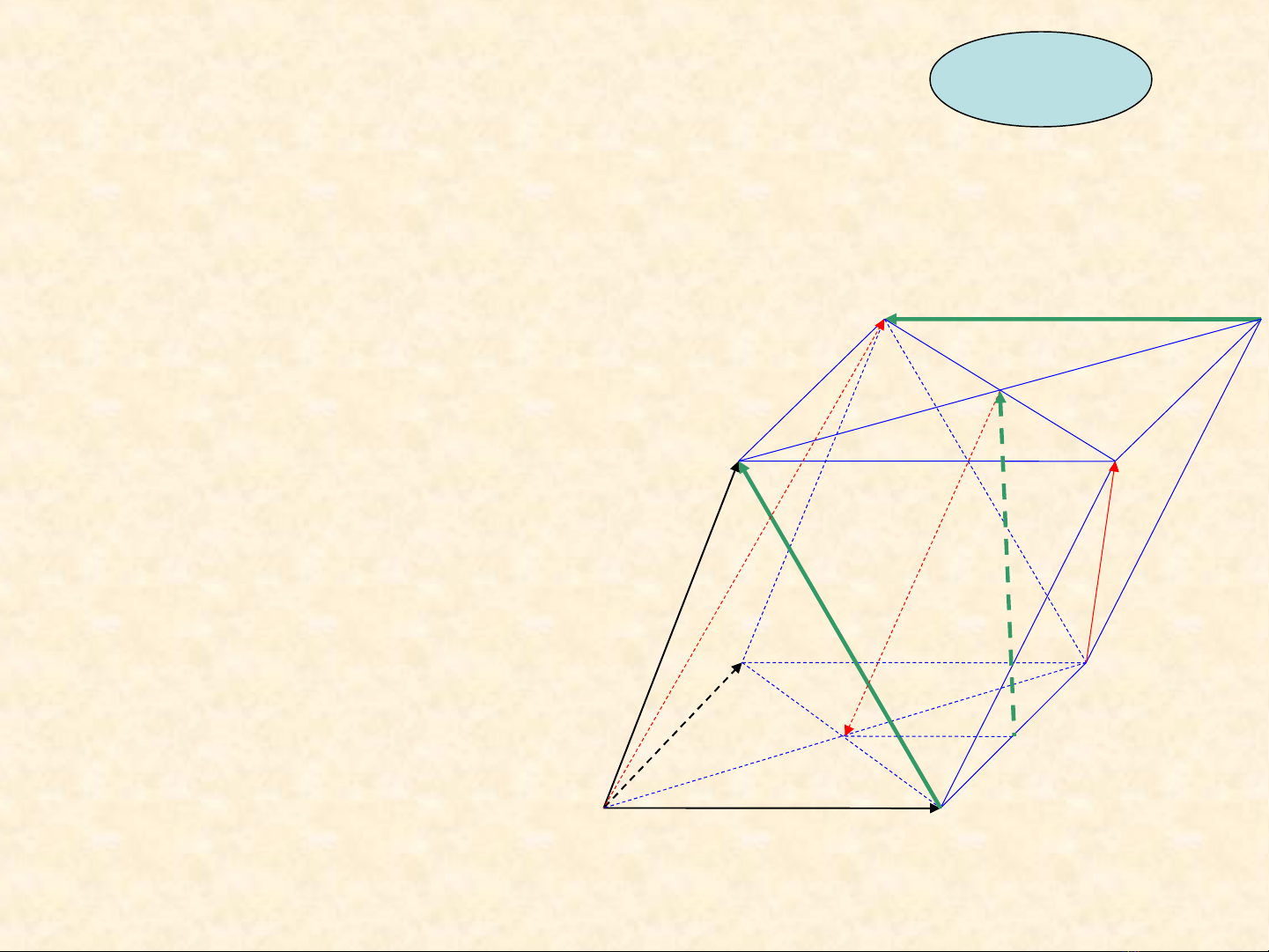
Ví d 4ụ
Cho hình h pộ
.ABCD A B C D
′ ′ ′ ′
có tâm hai đáy l n l t là O ầ ượ
và O/.M là trung đi m c a ể ủ
BC,các vec t ơ
, ,AB a AD b AA c
′
= = =
uuur r uuur r uuur r
Hãy bi u di n các vec tể ễ ơ
, , , , ,AD O O CC BA C D O M
′ ′ ′ ′ ′ ′
uuur uuuur uuuur uuur uuuur uuuur
theo
r i suy ra các b ba vec t đ ng ph ng : ồ ộ ơ ồ ẳ
( ) ( )
, , ; , ,AD O O CB BA C D O M
′ ′ ′ ′ ′ ′ ′
uuuur uuuur uuur uuur uuuur uuuur