Bài giảng Dự báo và phân tích dữ liệu - Phùng Thanh Bình

Chia sẻ: Fvdx Fvdx | Ngày: | Loại File: PDF | Số trang:33

Thêm vào BST

Báo xấu

189
lượt xem 30
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng Dự báo và phân tích dữ liệu nhằm giới thiệu phương pháp luận Box-Jenkins, mô hình AR(p), mô hình MA(q) Mô hình ARMA(p,q) Mô hình ARIMA(p,d,q) Mô hình SARIMA, và các ví dụ minh họa.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Dự báo và phân tích dữ liệu - Phùng Thanh Bình

AutoRegressive Integrated Moving Average Dự báo và Phân tích dữ liệu (12/11/2013) Phùng Thanh Bình ptbinh[a-còng]ueh.edu.vn
NỘI DUNG  Giới thiệu  Phương pháp luận Box-Jenkins  Mô hình AR(p)  Mô hình MA(q)  Mô hình ARMA(p,q)  Mô hình ARIMA(p,d,q)  Mô hình SARIMA  Ví dụ minh họa
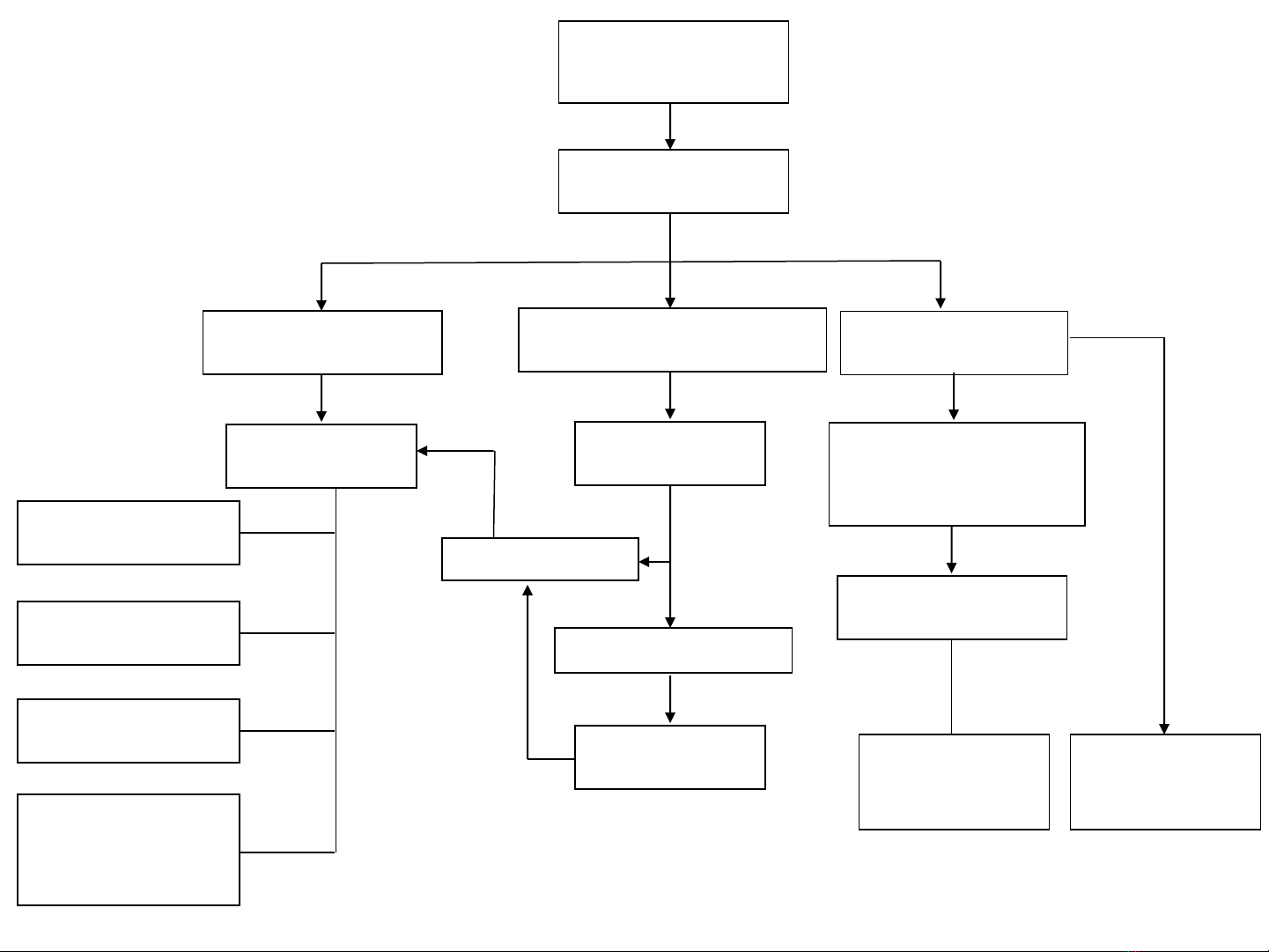
BOX-JENKINS Yt METHODOLOGY Ln(Yt) Stationary Nonstationary Seasonal p, q ∆LnYt Seasonal difference Diagnostic Checking AR(p) Stationary p, q, P, Q MA(q) NonStationary ARMA(p,q) ∆2LnYt Holt- SARIMA Winters Practical ARMA(p,q) Comparison
BOX-JENKINS METHODOLOGY Step 1 Calculate the ACF and PACF of the raw data, and check whether the series is stationary or not. If the series is stationary go to step 3, if not go to step 2. Step 2 Take the log and the 1st diff.of the raw data and calculate the ACF and PACF for the first logarithic differenced series. Step 3 Examine the graphs of the ACF and PACF and determine which models would be good starting points. Step 4 Estimate those models. Step 5 Diagnostic checking for each of these estimated models: a) Check to see if the parameter of the longest lag is significant. If not, then you probably have too many parameters, and should decrease the order of p and/or q. b) Check the ACF and PACF of the errors. If the model has at least enough parameters, then all ACFs and PACFs will be insignificant. c) Check the AIC and SBC together with the adj-R2 of the estimated models to detect which model is the parsimonious one (i.e., the one that minimizes AIC and SBC and has the highest adj-R2). d) Check the RMSE and compare the fitted – actual value graphs (especially at turning points). If the series is highly volatile (e.g., stock prices, gold prices, and other commodity prices), we sometimes check whether the ARCH effects exist. If yes, we should apply the ARCH/GARCH models for the data. Step 6 If changes in the original model are needed, go back to step 4.
AUTOREGRESSIVE (AR) MODEL  Giả sử Yt là một chuỗi dừng  Mô hình AR(p) có dạng sau đây: Yt = B0 + B1Yt-1 + … + BpYt-p + ut (1) ut: white noise error term  Độ trễ p được xác định theo lối thực nghiệm, dựa vào các tiêu chí như AIC, hoặc theo PACF!  PACF? Partial AutoCorrelation Function
AUTOREGRESSIVE (AR) MODEL  PACF3 Yt = b0 + b1Yt-1 + b2Yt-2 + b3Yt-3 + et (2) Yt-3 = c0 + c1Yt-1 + c2Yt-2 + v3 (3) Yt = a0 + b3v3 + rt (4)  PACFk Yt = b0 + b1Yt-1 + … + bkYt-k + et (5) Yt-k = c0 + c1Yt-1 + … + ct-k-1Yt-k-1 + vk (6) Yt = a0 + bkvk + rt (7)
AUTOREGRESSIVE (AR) MODEL  AR(p) phù hợp với chuỗi thời gian có dạng: • Các hệ số tự tương quan (ACF) giảm từ từ xuống giá trị 0; và • Các hệ số tự tương quan riêng (PACF) sẽ giảm xuống giá trị 0 ngay sau khi độ trễ p.
AR(1) AR(1) AR(2) AR(2)
MOVING AVERAGE (MA) MODEL  Giả sử Yt là một chuỗi dừng  Mô hình MA(q) có dạng sau đây: Yt = + ut + C1ut-1 + … + Cqut-q (8)  Độ trễ q được xác định theo lối thực nghiệm, dựa vào các tiêu chí như AIC, hoặc theo ACF!  ACF? AutoCorrelation Function
AUTOREGRESSIVE (AR) MODEL  MA(q) phù hợp với chuỗi thời gian có dạng: • Các hệ số tự tương quan (ACF) sẽ giảm xuống giá trị 0 ngay sau khi độ trễ q; và • Các hệ số tự tương quan riêng (PACF) giảm từ từ xuống giá trị 0.
MA(1) MA(1) MA(2) MA(2)
AUTOREGRESSIVE MOVING AVERAGE(ARMA) MODEL  Giả sử Yt là một chuỗi dừng  Mô hình ARMA(p,q) có dạng sau đây [kết hợp (1) và (8)]: Yt = A + B1Yt-1 + … + BpYt-p + ut + C1ut-1 + … + Cqut-q (9)  Độ trễ p và q được xác định như ở mô hình AR và MA.
TỔNG QUÁT ACF PACF Decays exponentially or Significant spikes AR(p) with damped sine wave through lag p pattern or both Significant spikes Decays exponentially or MA(q) through lag q with damped sine wave pattern or both ARMA(p,q) Exponential decay Exponential decay
ARMA(1,1)
ARIMA(p,d,q)  “Integrated of order d”?  Xác định p, d, q như thế nào?  So sánh giữa các mô hình?  Xem hệ số gắn với độ trễ xa nhất có ý nghĩa thống kê hay không  Giản đồ tự tương quan phần dư  Các tiêu chí AIC, SIC  RMSE, MAE, …  Quan sát đồ thị, …  XÁC ĐỊNH MÔ HÌNH ARIMA THỰC TẾ?
ARIMA(p,d,q)  VÍ DỤ (Y là một chuỗi dừng): • AR(2) hoặc ARMA(2,0) ls Y c AR(1) AR(2) • MA(3) hoặc ARMA(0,3) ls Y c MA(1) MA(2) MA(3) • ARMA(1,2) ls Y c AR(1) MA(1) MA(2)
ARIMA(p,d,q)  VÍ DỤ (Y là một chuỗi dừng ở sai phân bậc 1): • ARIMA(2,1,0) ls D(Y) c AR(1) AR(2) • ARIMA(0,1,3) ls D(Y) c MA(1) MA(2) MA(3) • ARIMA(1,1,2) ls D(Y) c AR(1) MA(1) MA(2)
ARIMA(p,d,q)  VÍ DỤ [log(Y) là một chuỗi dừng ở sai phân bậc 1]: • ARIMA(2,1,0) ls D(log(Y)) c AR(1) AR(2) • ARIMA(0,1,3) ls D(log(Y)) c MA(1) MA(2) MA(3) • ARIMA(1,1,2) ls D(log(Y)) c AR(1) MA(1) MA(2)
SARIMA(p,d,q;P,Q)  Dữ liệu tháng: P = 12, Q = 12  Dữ liệu quý: P = 4, Q = 4  VÍ DỤ (Y là chuỗi dừng, theo quý): • SARIMA(2,0,0;4,0) ls Y c AR(1) AR(2) SAR(4) • SAMRIA(0,0,3;4,4) ls Y c MA(1) MA(2) MA(3) SAR(4) SMA(4)
ARIMA thực tế  VÍ DỤ (Y là chuỗi dừng, p = 3, 7, 15; q = 1, 5, 15) ls Y c AR(3) AR(7) AR(15) MA(1) MA(5) MA(15) (10) Giả sử hệ số của MA(15) không có ý nghĩa thống kê, và hệ số ACF7 ≠ 0, và PACF5 ≠ 0), ta ước lượng lại như sau: ls Y c AR(3) AR(5) AR(7) AR(15) MA(1) MA(5) MA(7) (11)