PHÂN TÍCH DỮ LIỆU
KIỂM ĐỊNH GIẢ THUYẾT,
HỒI QUY
# Phân tích tương quan - 2
biến định lượng
-Mối liên quan giữa hai biến định lượng có thể
được biểu thị dưới dạng biểu đồ chấm và hệ số
tương quan
-Nếu cả hai biến đều có phân bố chuẩn, thì hệ số
tương quan Pearson’s là có giá trị
- Nếu không,cần phải sử dụng hệ số tương quan
Spearman’s
-Từ thực đơn dọc chọn:
Analyse/ Correlate/ Bivariate
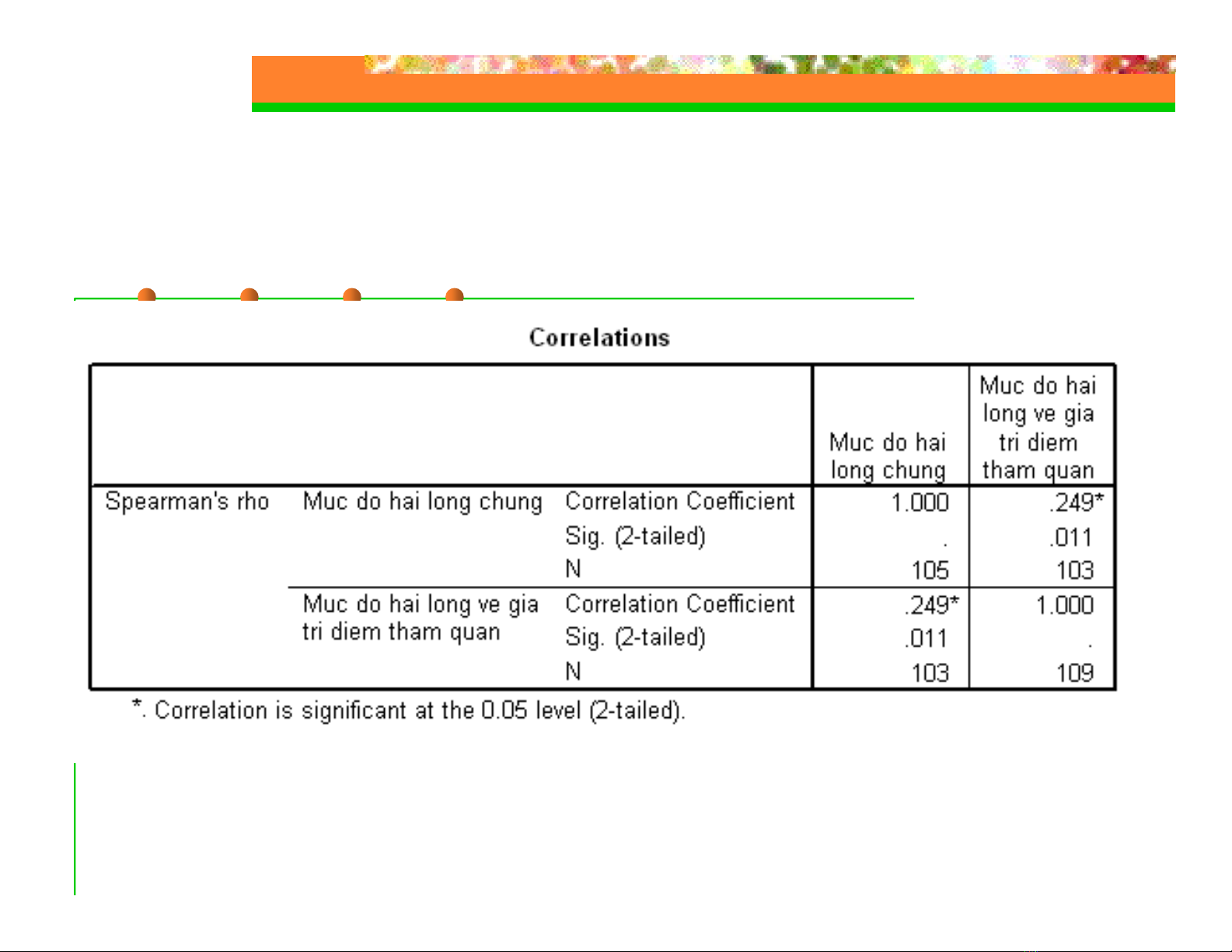
# Hệ số tương quan
Kiểm định trung bình tổng thể
# Kiểm định giả thuyết về trung bình
của một tổng thể:
Nếu muốn so sánh giá trị trung bình của
một tổng thể với một giá trị cụ thể nào đó,
sử dụng One-sample T-test
-Vào menu, chọn Analyze/ Compare
Means/ One-sample T-test
-Chọn biến đưa vào khung Test Variable
- Khai báo Test Value
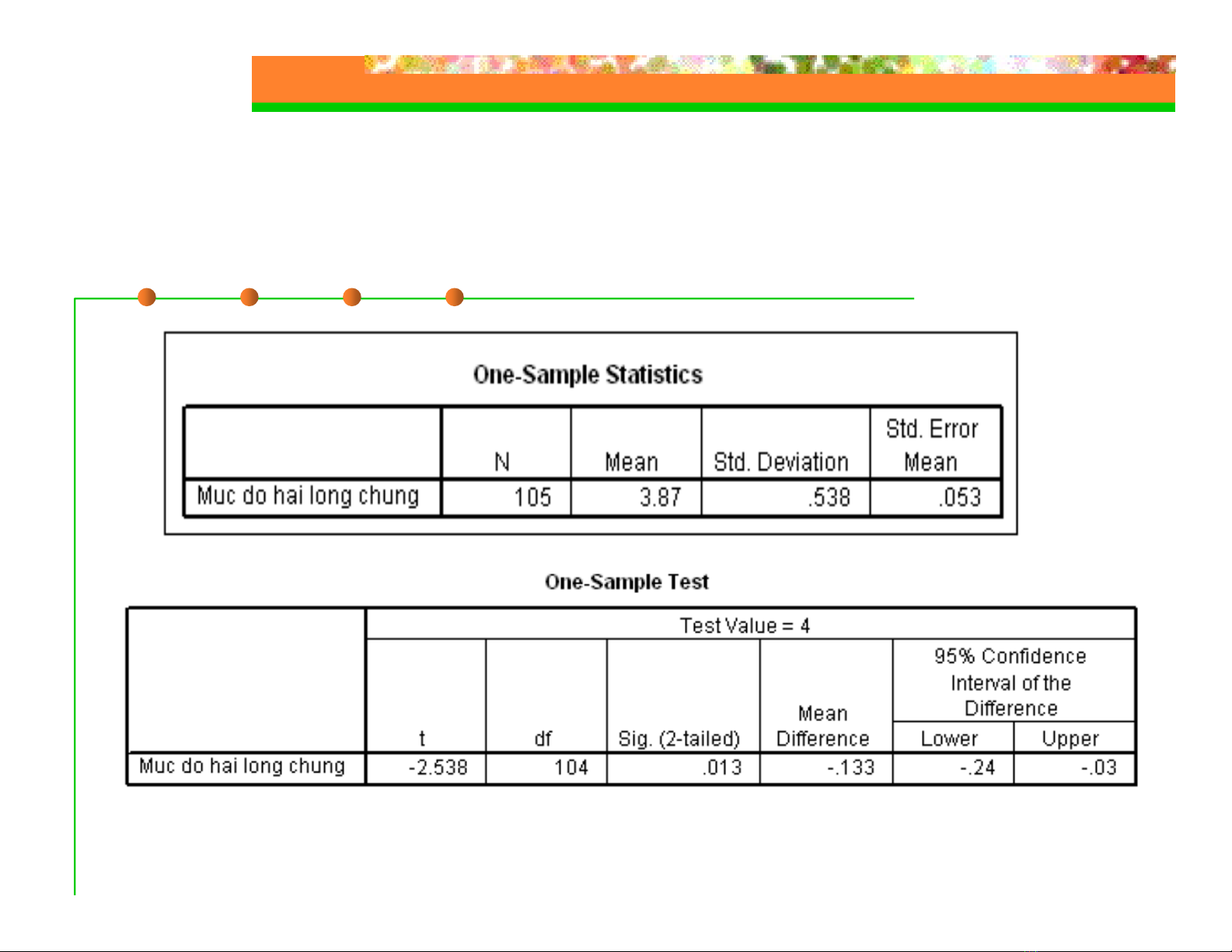
# Ví dụ: Kiểm định One-sample
T-test