I. B n ch t c a đa c ng tuy nả ấ ủ ộ ế
Đa c ng tuy n là t n t i m i quan h ộ ế ồ ạ ố ệ
tuy n tính gi a m t s ho c t t ế ữ ộ ố ặ ấ
c các bi n đc l p trong mô ả ế ộ ậ
hình.
Xét hàm h i qui k bi n :ồ ế
Yi = 1+ 2X2i + …+ kXki + Ui
- N u t n t i các s ế ồ ạ ố 2, 3,…,k không
đng th i b ng 0 sao cho :ồ ờ ằ
Ch ng 6ươ
Đa c ng tuy nộ ế
2X2i + 3X3i +…+ kXki + a = 0
(a : h ng s )ằ ố
Thì gi a các bi n đc l p x y ra hi n ữ ế ộ ậ ả ệ
t ng ượ đa c ng tuy n hoàn h oộ ế ả .
- N u t n t i các s ế ồ ạ ố 2, 3,…,k không
đng th i b ng 0 sao cho :ồ ờ ằ
2X2i + 3X3i +…+ kXki + Vi = 0
(Vi : sai s ng u nhiên)ố ẫ
Thì gi a các bi n đc l p x y ra hi n ữ ế ộ ậ ả ệ
t ng ượ đa c ng tuy n không hoàn ộ ế
Ta có : X3i = 5X2i có hi n t ng ệ ượ
c ng tuy n hoàn h o gi a Xộ ế ả ữ 2 và X3 và
r23 =1
X4i = 5X2i + Vi có hi n t ng ệ ượ
c ng tuy n không hoàn h o gi a Xộ ế ả ữ 2
và X , có th tính đc rể ượ = 0.9959.
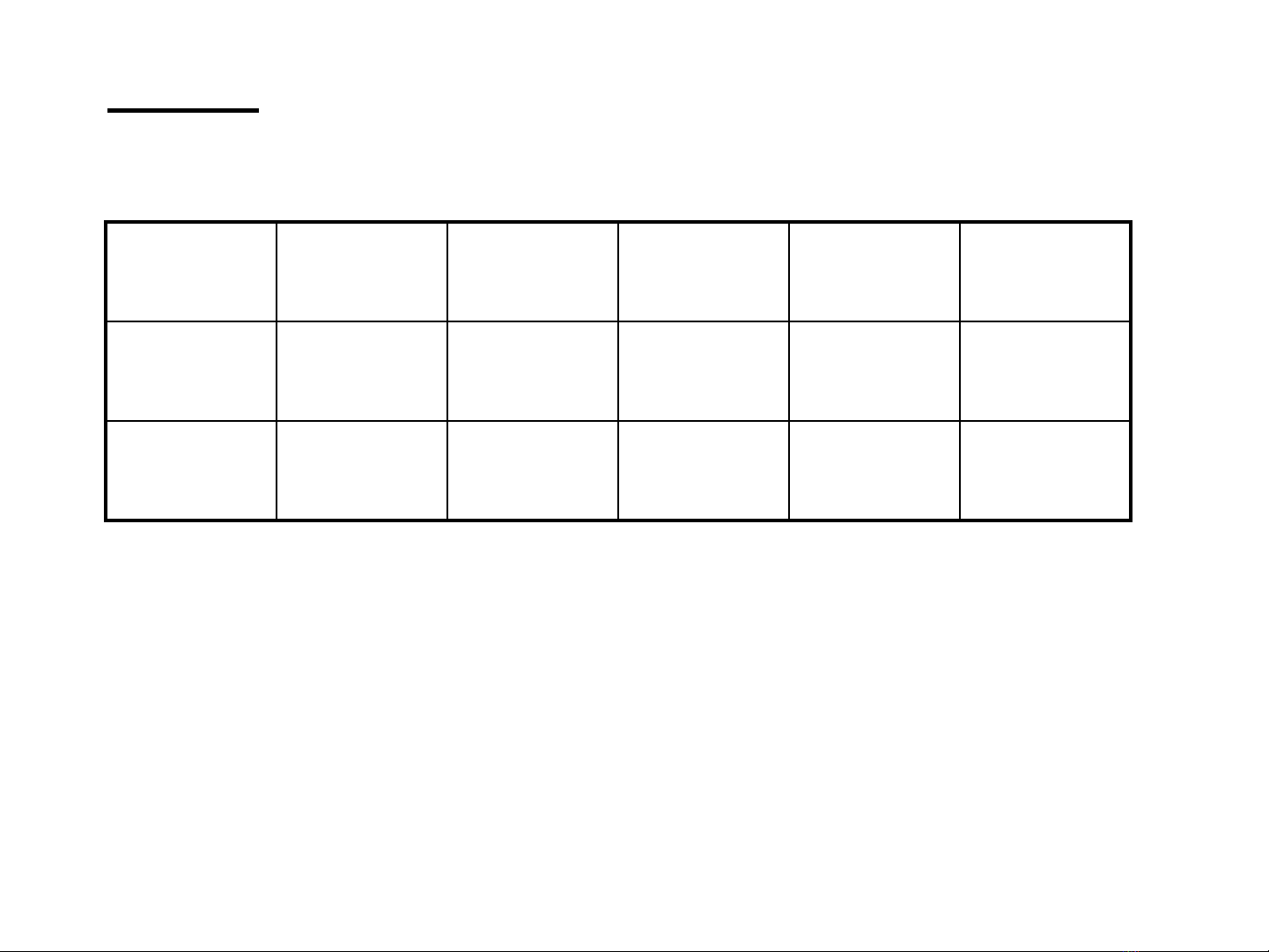
X210 15 18 24 30
X350 75 90 120 150
X452 75 97 129 152
Ví dụ : Yi = 1+2X2i+3X3i+ 4X4i + Ui
V i s li u c a các bi n đc l p :ớ ố ệ ủ ế ộ ậ
II. c l ng trong tr ng h p có Ướ ượ ườ ợ
đa c ng tuy nộ ế
1.Tr ng h p có đa c ng tuy n hoàn ườ ợ ộ ế
h oả
Xét mô hình :Yi = 1+2X2i+3X3i+ Ui (1)
Gi s : Xả ử 3i = X2i x3i = x2i. Theo OLS:
2
3i2i
2
3i
2
2i
i2i3i2i
2
2ii3i
2
3i2i
2
3i
2
2i
i3i3i2i
2
3ii2i
)xx(xx
yxxxxyx
)xx(xx
yxxxxyx
3
2
ˆ
ˆ
β
β
Tuy nhiên n u thay Xế3i = X2i vào hàm
h i qui (1), ta đc :ồ ượ
Yi = 1+2X2i+3 X2i + Ui
Hay Yi = 1+ (2+ 3) X2i + Ui (2)
c l ng (2), ta có :Ướ ượ
0
0
λ)λ(
)λ)(λ()λ(
ˆ
22
2
2
22
2i
2
2i
2
2i
i2i
2
2i
2
2ii2i
)x(xx
yxxxyx
β
0
0
ˆ
3
β
3201
ˆˆˆ
,
ˆβλβββ
Thay x3i = 2x2i vào công th c :ứ
T ng t :ươ ự