CH NG 6ƯƠ
CH NG 6ƯƠ
HI N T NG ĐA C NG TUY NỆ ƯỢ Ộ Ế
HI N T NG ĐA C NG TUY NỆ ƯỢ Ộ Ế
(MULTICOLLINEARITY)
(MULTICOLLINEARITY)
2
1. Hiểu bản chất và hậu quả
của đa cộng tuyến
2. Biết cách phát hiện đa cộng
tuyến và biện pháp khắc
phục
MỤC
TIÊU
ĐA C NG TUY NỘ Ế
N I DUNGỘ
3
Bản chất, nguyên nhân của đa cộng tuyến
1
Ước lượng các tham số
2
3
Phát hiện đa cộng tuyến4
Khắc phục đa cộng tuyến
5
Hậu quả
4
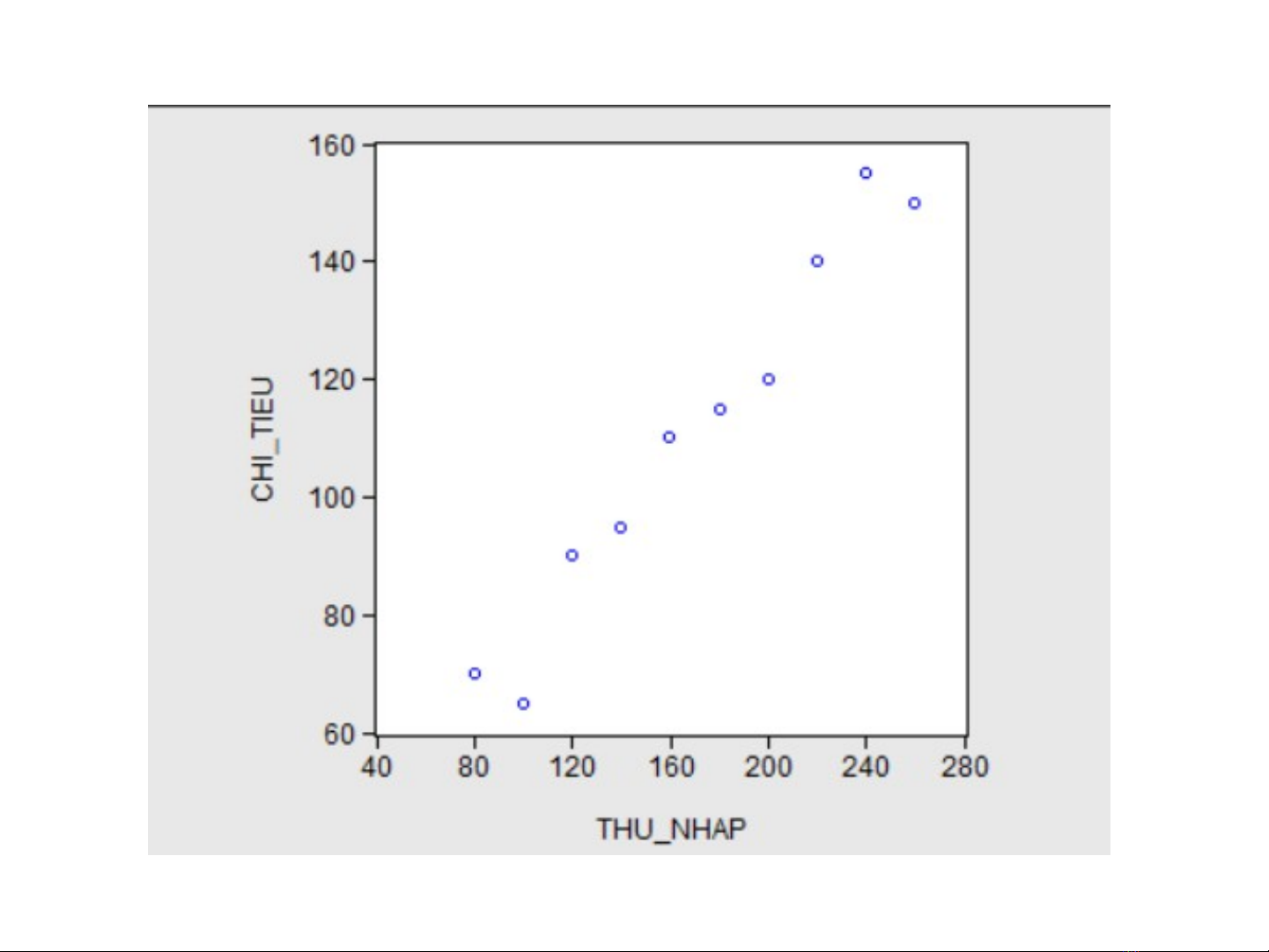
Thu nhập
Sự giàu
có Chi tiêu
80 810 70
100 1009 65
120 1273 90
140 1425 95
160 1633 110
180 1876 115
200 2052 120
220 2201 140
240 2435 155
260 2686 150
Nguồn: Ramu Ramanathan
5