Bài giảng Lý thuyết đồ thị: Chương 6 - ThS. Trần Quốc Việt

Chia sẻ: _ _ | Ngày: | Loại File: PDF | Số trang:44

Thêm vào BST

Báo xấu

15
lượt xem 2
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng Lý thuyết đồ thị: Chương 6 Một số ứng dụng, cung cấp cho người đọc những kiến thức như: Bài toán luồng cực đại (Max-flow problem); Bài toán ghép cặp (Matching problem);... Mời các bạn cùng tham khảo!

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

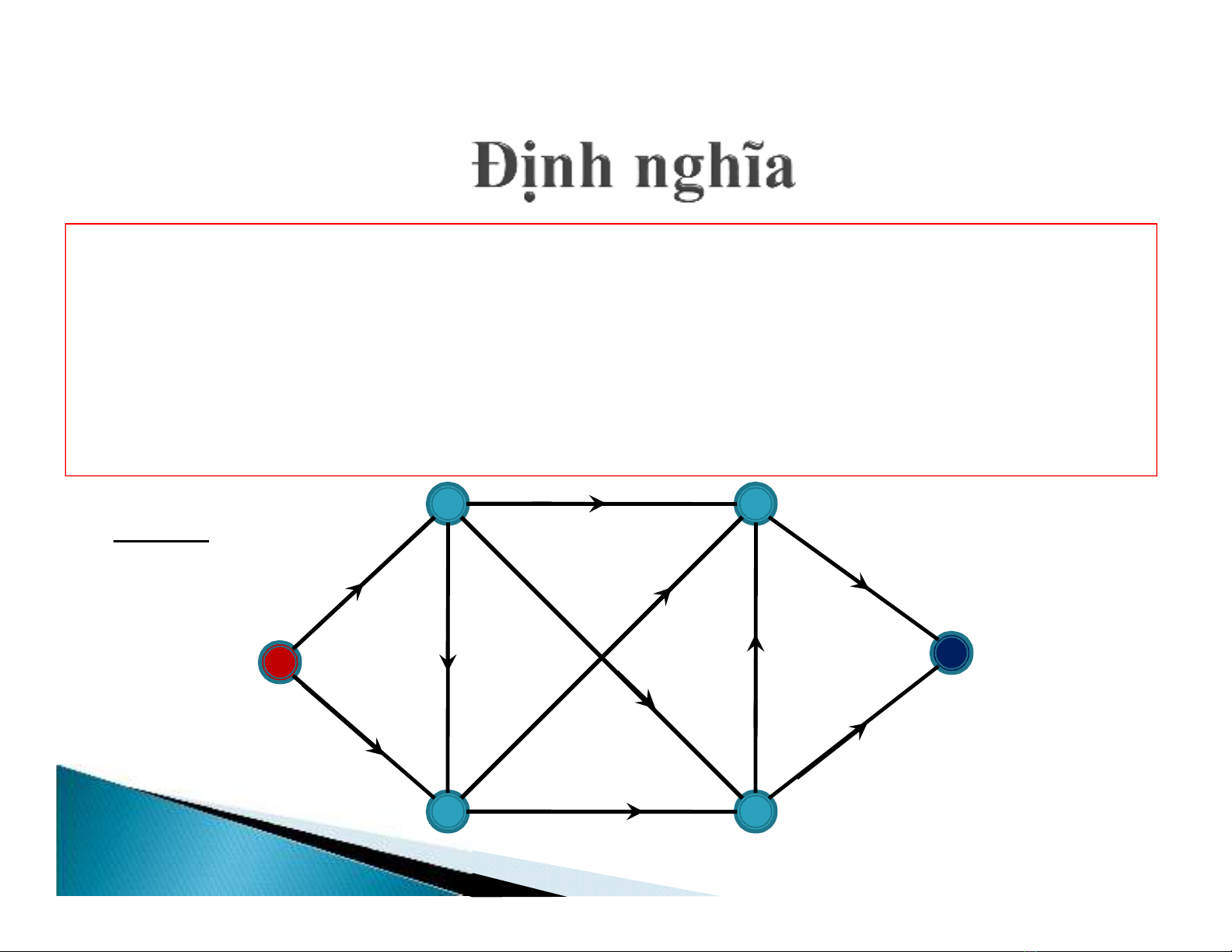
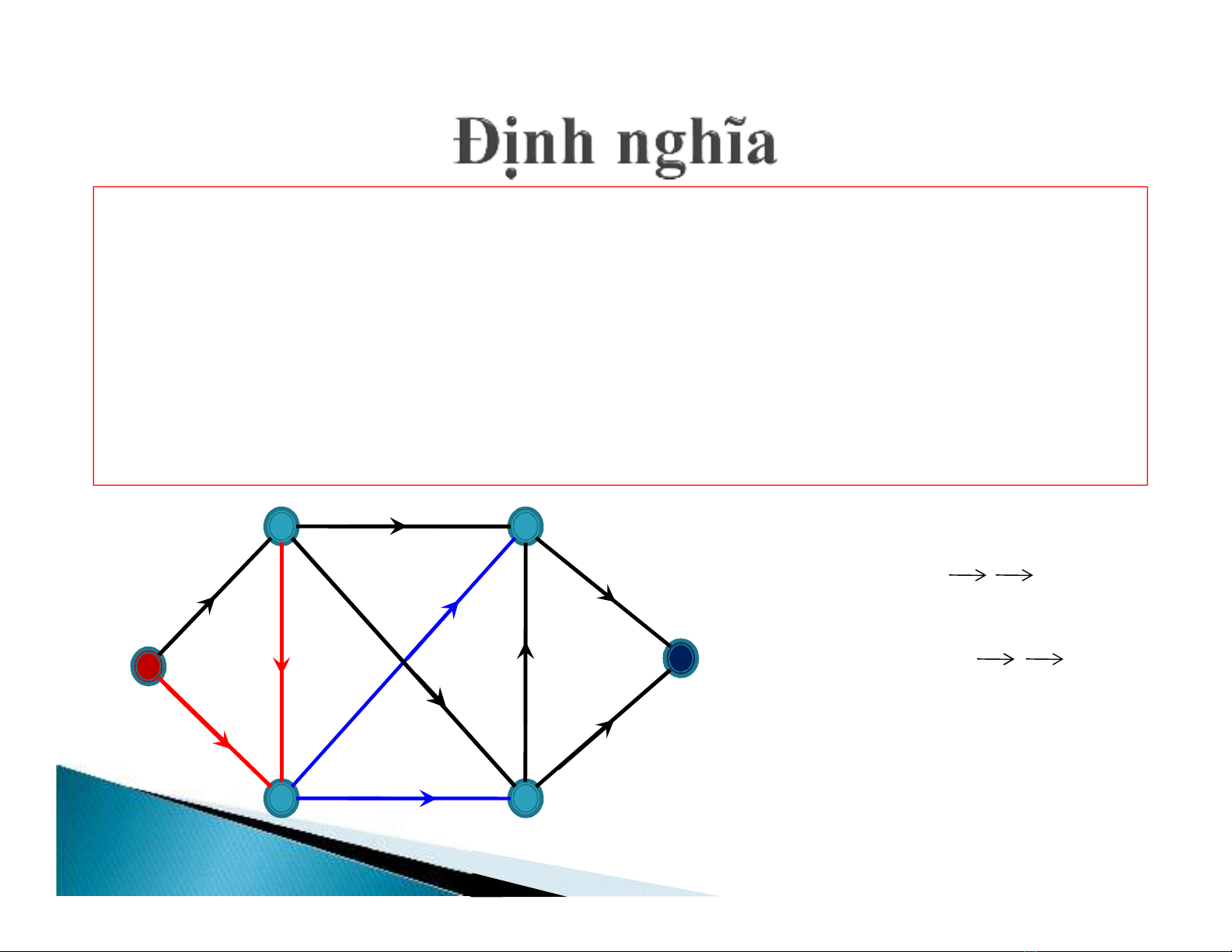
Nội dung Text: Bài giảng Lý thuyết đồ thị: Chương 6 - ThS. Trần Quốc Việt

CHƯƠNG 6 GV: TRẦN QUỐC VIỆT 1
Giới thiệu 2 ứng dụng:  Bài toán luồng cực đại (Max-flow problem)  Bài toán ghép cặp (Matching problem) 2
3
 Mạng (network) là một đồ thị có hướng có trọng số G = (V,E) trên đó ta chọn một đỉnh gọi là đỉnh phát (source vertex) và 1 đỉnh gọi là đỉnh thu (sink vertex). 3 Ví dụ 5 5 2 6 2 source sink 8 4 4 3 4
 Một mạng G = (V,E) với đỉnh phát là a, đỉnh thu là z, c(e)  N là trọng số của cung e. Với mỗi đỉnh x, ta đặt: In(x) = {e  E | e tới trong x} Out(x) = {e  E | e tới ngoài x} b 3 d 5 5 In(c)={ac, bc} 2 6 2 a z Out(c)={cd, ce} 8 4 4 c 3 e 5
 Một hàm tải (flow function) trên G được định nghĩa bởi ánh xạ: φ: E  N thỏa các điều kiện (i) 0 ≤ φ(e) ≤ c(e), e  E (Giới hạn của luồng) (i) φ(e) = 0, e  In(a)  Out(z) (Giá trị luồng) (iii)   (e)    (e) ,  x  V \ a, z bằngluồng) e In(x) eOut(x) (Cân 6
(fa) = 0 (zg) = 0 b d (ab) = 4 3,1 c[u,v]/f[u,v] (ac) = 1 5,4 2,1 5,4 (fc) = 0 6,2 2,1 z (gc) = 0 a 4,1 (bd) = 1 4,1 8,2 (be) = 1 4,0 c 3,1 (2,0) (bc) = 2 e (cd) = 2 3,0 1,0 (ce)=1 f g (dz) = 4 (ez) = 1 (ed) = 1 7
 Một phép cắt (cut) xác định bởi 1 tập hợp con P của V, ký hiệu (P, P ) là tập hợp: (P, P ) = { xy | x  P và y  P } Trong đó P  V \ P  Phép cắt (P, P ) gọi là 1 phép cắt a-z nếu aP và z P  Trọng số (capacity) của một phép cắt được định nghĩa là: c(P, P)   c(e) 8 e(P,P )
b 3 d 5 5 2 6 2 a z 8 4 4 c  P={a,b, c} 3 e  P={d, e,z}  (P,P)={bd,be,cd,ce}  c(P,P)=16 9
Gọi  là một hàm tải trên mạng G và P  V\{a,z} thì:   (e)    (e) e(P, P ) e ( P , P) Ví dụ: b 3,1 d P 5,4 5,4 2,1 2,1 a 6,2 z 4,1 8,2 4,1 4,0 3,1 (2,0) c e 3,0 1,0 f g 10
 Với mọi hàm tải φ trên mạng G, lượng tải khỏi a bằng lượng tải vào z, nghĩa là:   (e)    (e) eOut(a) eIn(z) b d 3,1 5,4 5,4 2,1 2,1 a 6,2 z 4,1 8,2 4,1 4,0 (2,0) 3,1 c e 3,0 1,0 f g 11
 Đặt P = V \ {a,z}, khi đó:  (e)   (e)   (e)   (e) eOut(a) eIn(z) e( P ,P) e(P,P ) 12
 Với mọi hàm tải φ và với mọi phép cắt a-z trong mạng G, ta có: |  |  c(P, P ) 13
 Thêm vào G một đỉnh a0 và cạnh a0a (hướng từ a0 đến a), c(a0a)=. Ta được mạng G’. Trong G’ đặt ’(a0a) = |  | và  ’(e) = (e), eE Ta có: |  ||  ' |   ' (e)    ' (e) e( P {a 0 }, P) e(P, P {a 0 })    (e)   c(e)  c(P, P) e(P, P ) e(P, P ) 14
 Với mọi hàm tải φ và mọi phép cắt a-z trong mạng G. |φ|= c(P, P ) nếu và chỉ nếu thỏa 2 điều kiện: (i)  e  ( P , P),  (e)  0 (ii)  e  (P, P ),  (e)  c(e)  Khi |  |  c(P, P ) thì  là hàm tải có tải trọng lớn nhất và (P, P ) là phép cắt a-z có trọng số nhỏ nhất 15
 Cho một mạng G, đỉnh phát a và đỉnh thu z, với một phép căt a-z ( P, P )  Một chuyền a-z K là một đường đi vô hướng nối a với z  Ký hiệu s(e) = c(e)-(e) gọi là độ lệch tải của e  Ta định nghĩa:  : e K   K (e)   : e K và có hướng từ a đến z -   : e K và e có hướng từ z đến a 16
Input: Mạng G, đỉnh phát a và đỉnh thu z Output: Tập P của phép cắt a-z tối thiểu (P, P )
Bắt đầu bằng 1 hàm tải  bất kỳ trên G 1. Đánh dấu mọi đỉnh đều chưa xét, gán nhãn cho a là (-,(a)) với (a)=. Đặt p0=a. 2. Xét p0. a. Cạnh e=p0q với q chưa có nhãn và s(e)>0 thì gán nhãn cho q là (p0+, min((p0), s(e))) b. Cạnh e=qp0 với q chưa có nhãn và (e)>0 thì gán nhãn cho q là (p0-, min((p0), (e))) 3. Nếu đỉnh z đã được gán nhãn  4, ngược lại  5. 4. Xác định một dây chuyền (vô hướng) từ a đến z dựa vào thành phần thứ 1 của nhãn. Cập nhật lại  như sau: (e) = (e) + (z)  K(e). Về bước 1. 5. Tìm 1 đỉnh p đã có nhãn nhưng chưa xét. Nếu tồn tại p, đặt p0 = p,  bước 2. Ngược lại dừng.
 Sau khi thuật toán kết thúc. P là tập hợp các đỉnh đã có nhãn và đã xét. 19
G với hàm tải ban đầu: b 6,5 d 5,5 6,6 3,0 3,1 a z 6,1 5,2 c 1,1 e 20