Bài giảng Nguyên lý thống kê kinh tế: Chương 8 - TS. Hồ Ngọc Ninh

12/3/2013<br /> <br /> 8.1. Phân tích tương quan (Correlation Analysis)<br /> <br /> a) Khái niệm về tương quan<br /> <br /> Chương 8<br /> Phân tích tương quan và hồi quy<br /> <br /> Tương quan là thước đo thể hiện mối quan hệ tuyến<br /> tính giữa hai biến, nghĩa là 2 biến cùng biến động theo<br /> một cách nào đó.<br /> Phân tích tương quan là phương pháp dùng để đo mức<br /> độ của mối quan hệ tuyến tính giữa 2 biến và được thể<br /> hiện bằng hệ số tương quan.<br /> <br /> b) Hệ số tương quan<br /> r=<br /> <br /> Đặc điểm của hệ số tương quan<br /> <br /> n ( XY )  ( X )(  Y )<br /> [ n ( X 2 )  (  X ) 2 ][n (  Y 2 )  (  Y ) 2 ]<br /> <br /> <br /> <br /> Không có đơn vị tính<br /> <br /> <br /> <br /> Dao động trong khoảng từ –1 đến 1<br /> <br /> <br /> <br /> Càng gần –1, quan hệ nghịch, mạnh<br /> <br /> <br /> <br /> Càng gần 1, quan hệ thuận, mạnh<br /> <br /> <br /> <br /> Càng gần 0, quan hệ yếu<br /> <br /> <br /> <br /> Bằng 0, không có tương quan<br /> <br /> <br /> <br /> Bằng 1, tương quan dương hoàn hảo<br /> <br /> <br /> <br /> Bằng -1, tương quan âm hoàn hảo<br /> <br /> hoặc<br /> <br /> <br /> r=<br /> <br /> <br /> <br /> ( X  X ) (Y  Y )<br /> <br /> ( X  X )<br /> <br /> 2<br /> <br /> <br /> <br /> (Y  Y )<br /> <br /> 2<br /> <br /> 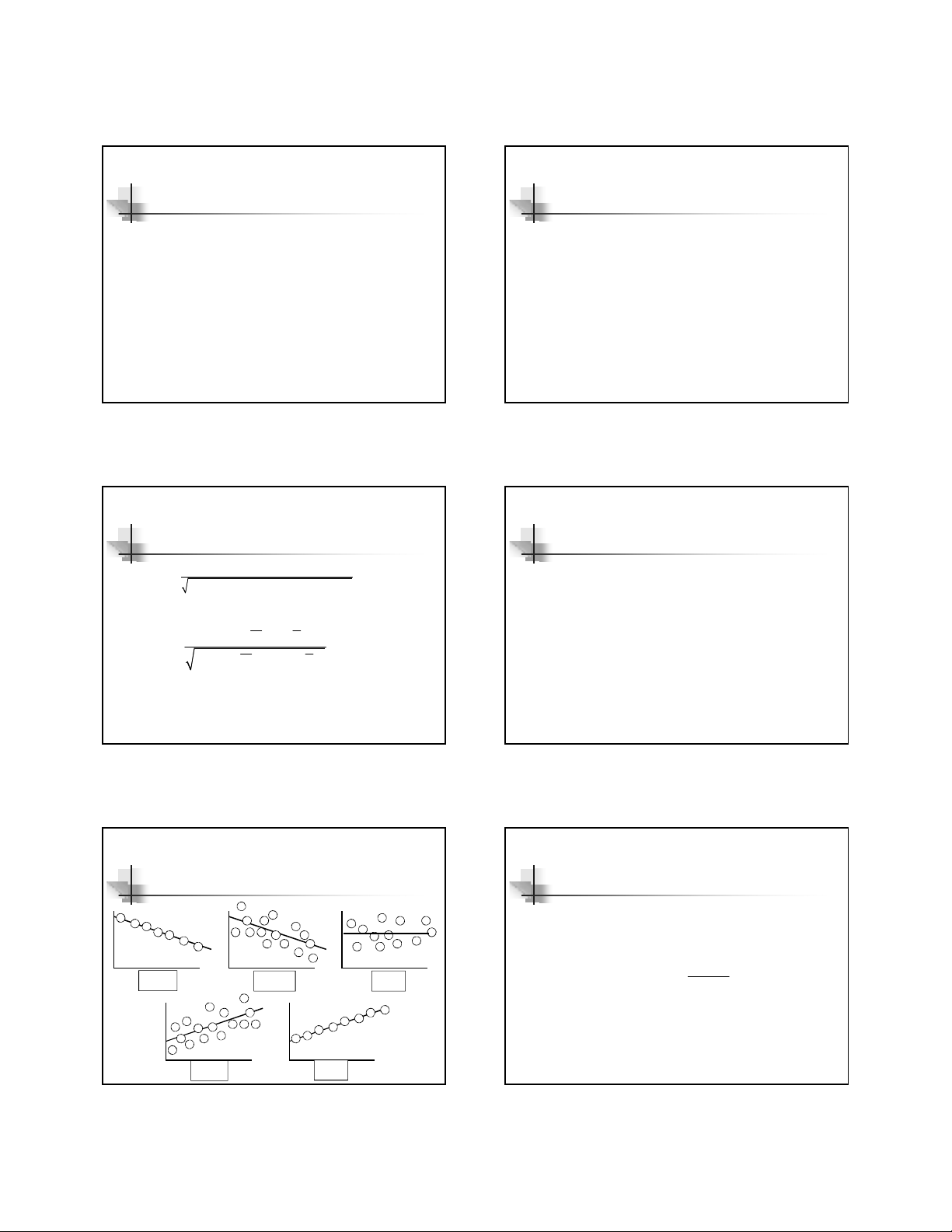Sự phân bố data với các hệ số tương<br /> quan khác nhau<br /> Y<br /> <br /> Y<br /> <br /> c) Tương quan hạng<br /> <br /> Y<br /> <br /> <br /> <br /> <br /> X<br /> <br /> r = -1<br /> <br /> X<br /> <br /> r = -.6<br /> <br /> X<br /> <br /> r=0<br /> <br /> <br /> <br /> <br /> Y<br /> <br /> Y<br /> <br /> r = .6<br /> <br /> X<br /> <br /> r=1<br /> <br /> Khi giá trị cụ thể của X và Y không có hoặc không<br /> chính xác.<br /> X và Y được xếp hạng theo độ lớn, tầm quan trọng<br /> hay một tiêu thức nào đó.<br /> 6 D 2<br /> <br /> Công thức  = 1 n ( n 2  1)<br /> D là chênh lệch về hạng của cặp giá trị X và Y tương<br /> ứng<br /> <br /> X<br /> <br /> 1<br /> <br /> 12/3/2013<br /> <br /> d) Kiểm định hệ số tương quan<br /> Giả thiết<br /> Ho:  =0 (không có tương quan)<br /> H1:  ≠0 (Có tương quan)<br /> Công thức<br /> t= r n2<br /> với (n-2) là bậc tự do<br /> 1 r<br />  Tra bảng phân phối Student<br />  Tương quan hạng tra bảng Spearman<br /> 2<br /> <br /> 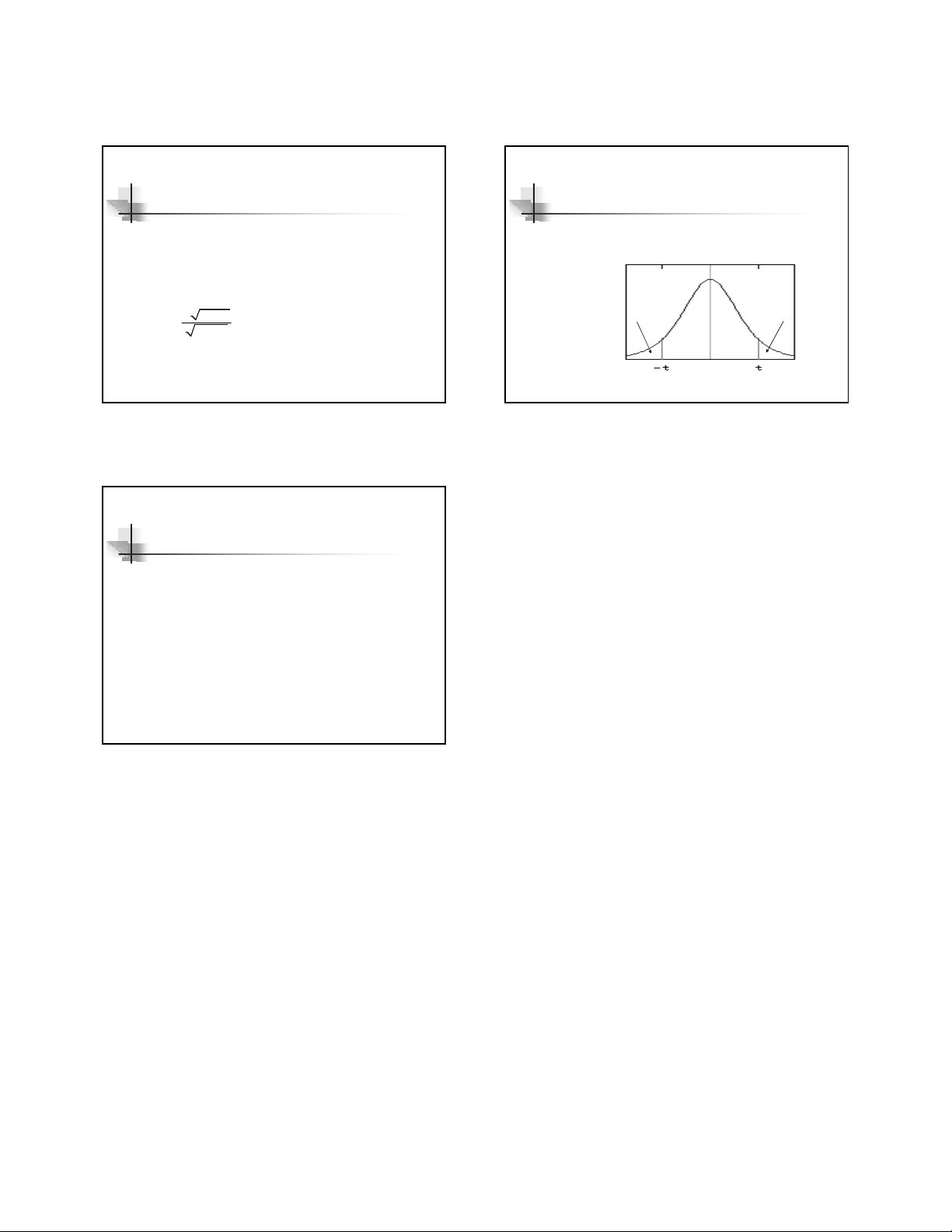Vùng bác bỏ hay chấp nhận hệ số tương quan<br /> <br /> Vùng bác bỏ<br /> <br /> Vùng bác bỏ<br /> <br /> (có tương quan)<br /> <br /> (có tương quan)<br /> Vùng Ho không thể bác bỏ<br /> (không có tương quan)<br /> <br /> 8.2. Phân tích hồi quy tuyến tính<br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> Khái niệm<br /> Phương pháp bình phương nhỏ nhất<br /> Sai số chuẩn của ước lượng<br /> Các giả định, giả thiết<br /> Khoảng tin cậy, khoảng dự báo<br /> Hệ số xác định<br /> <br /> 2<br /> <br />