Chƣơng 6. ĐẠO HÀM VÀ VI PHÂN CỦA HÀM MỘT BIẾN
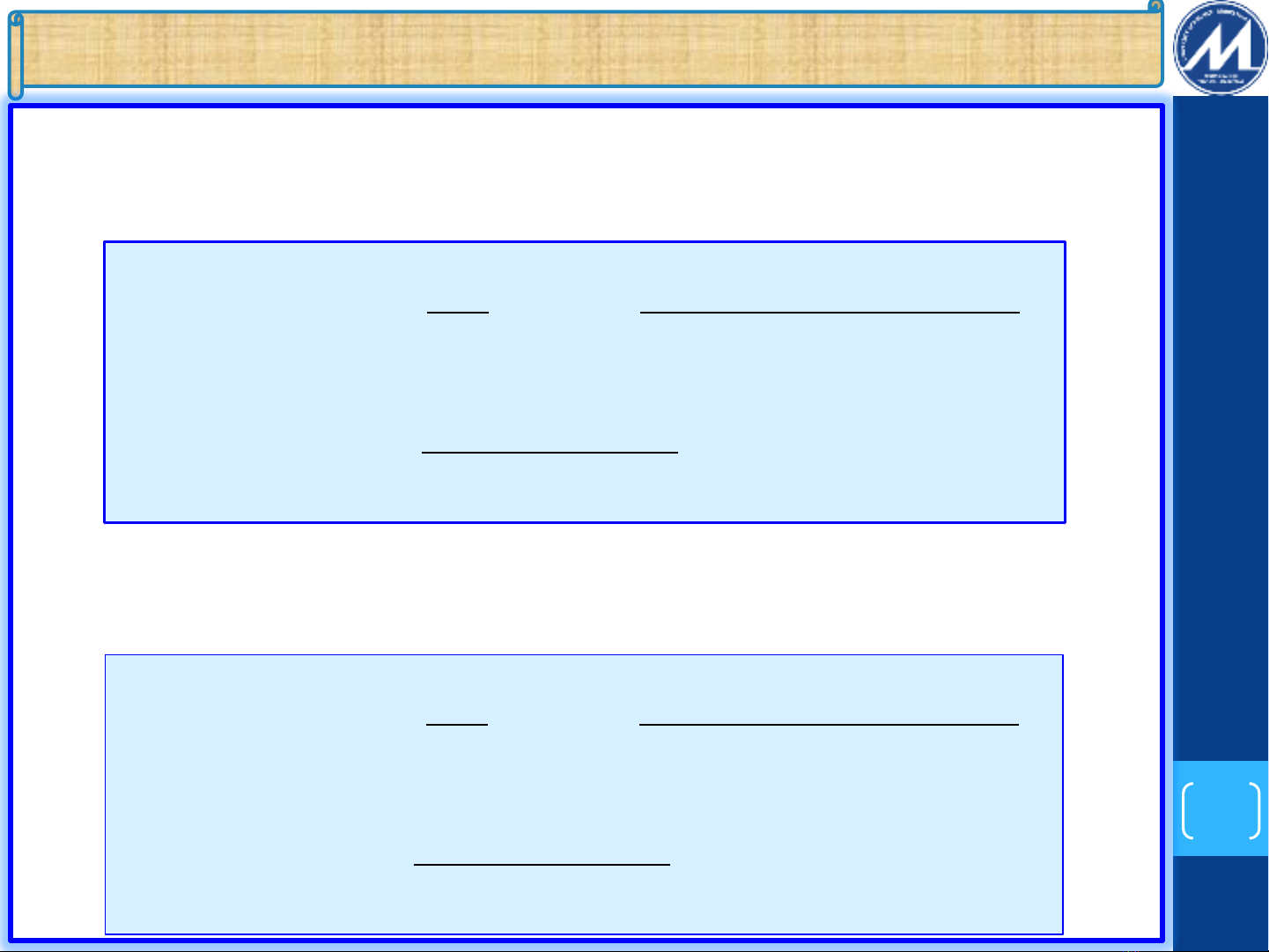
Hàm số được gọi là có đạo hàm bên phải tại ,
kí hiệu , nếu tồn tại giới hạn:
Hàm số được gọi là có đạo hàm bên trái tại , kí
hiệu , nếu tồn tại giới hạn:
Toán Cao Cấp - ThS. Lê Trường Giang
4
0
00
0x 0 x 0
0
xx 0
f x x f x
y
f x lim lim
xx
f x f x
lim xx
0
00
0x 0 x 0
0
xx 0
f x x f x
y
f x lim lim
xx
f x f x
lim xx





