KHOA: KHOA HỌC CƠ BẢN
BÀI TẬP THƯỜNG KỲ
HỌC PHẦN
TOÁN CAO CẤP A 2
(HỆ ĐẠI HỌC)
GVHD: ThS. PHAN MINH CHÍNH
KHOA:………………….Lớp:…….
Nhóm 1:
1. Nguyễn Như Ngọc (08881771)
2. Bùi Văn Tiệp (08267261)
Thành phố Hồ Chí Minh, 06/2009
Câu 1: Trên mặt phẳng tọa độ 0xy tìm tập hợp điểm biểu diễn số phức z thỏa điều
kiện:
a) Phần thực của z bằng -2
b) Phần thực của z thuộc khoảng (-1;2)
c)
1
z
d) 1<
z
2
Giải:
Ta có: z = a+bi trong đó a là phần thực và b là phần ảo
a) Phần thực của z bằng -2
z = -2+bi với b
R
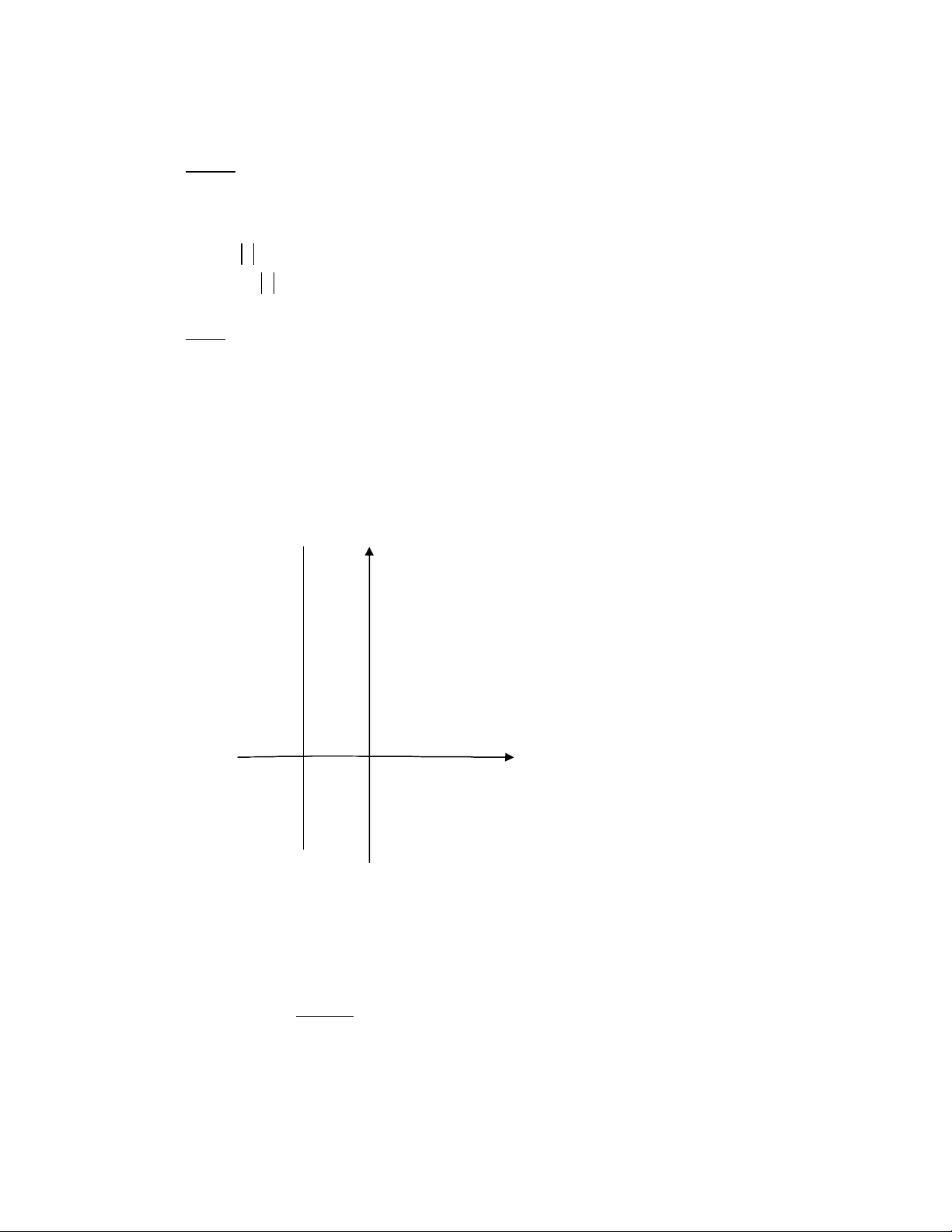
Tập hợp các điểm biểu diễn số phức z = -2+bi là đường thẳng có phương trình x = -
2 được biểu diễn trên đồ thị:
(y)
x = -2
(x)
-2 O
Vậy tập hợp điểm biểu diễn số phức có phần thực bằng -2 là đường thẳng
có phương trình x = -2
b) Phần thực của z thuộc khoảng (-1;2)
Tương tự như câu a ta ta có nhận xét:
Tập hợp những điểm biểu diễn số phức có phần thực bằng -1 là đường thẳng
có phương trình x = -1
Tập hợp những điểm biểu diễn số phức có phần thực bằng 2 là đường thẳng
có phương trình x = 2
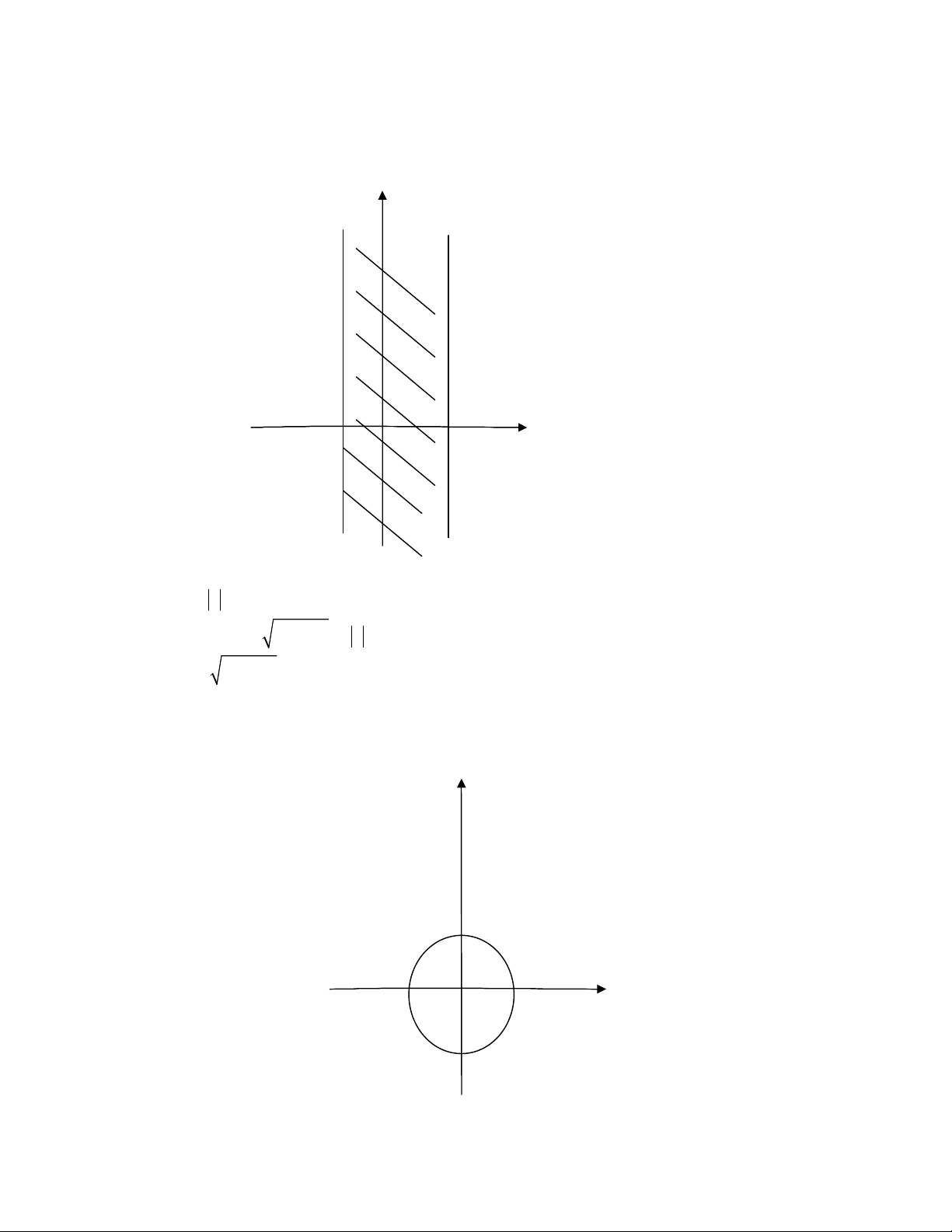
Do đó tập hợp những điểm biểu diễn số phức có phần thực thuộc khoảng (-1,2) là
phần mặt phẳng được giới hạn bởi 2 đường thẳng x = -1 và x = 2 như trên đồ thị:
(y)
x=-1 x=2
-1 0 2 (x)
c)
1
z
Ta có r =
2 2
a b
=
1
z
2 2
a b
= 1
a2 + b2 = 1
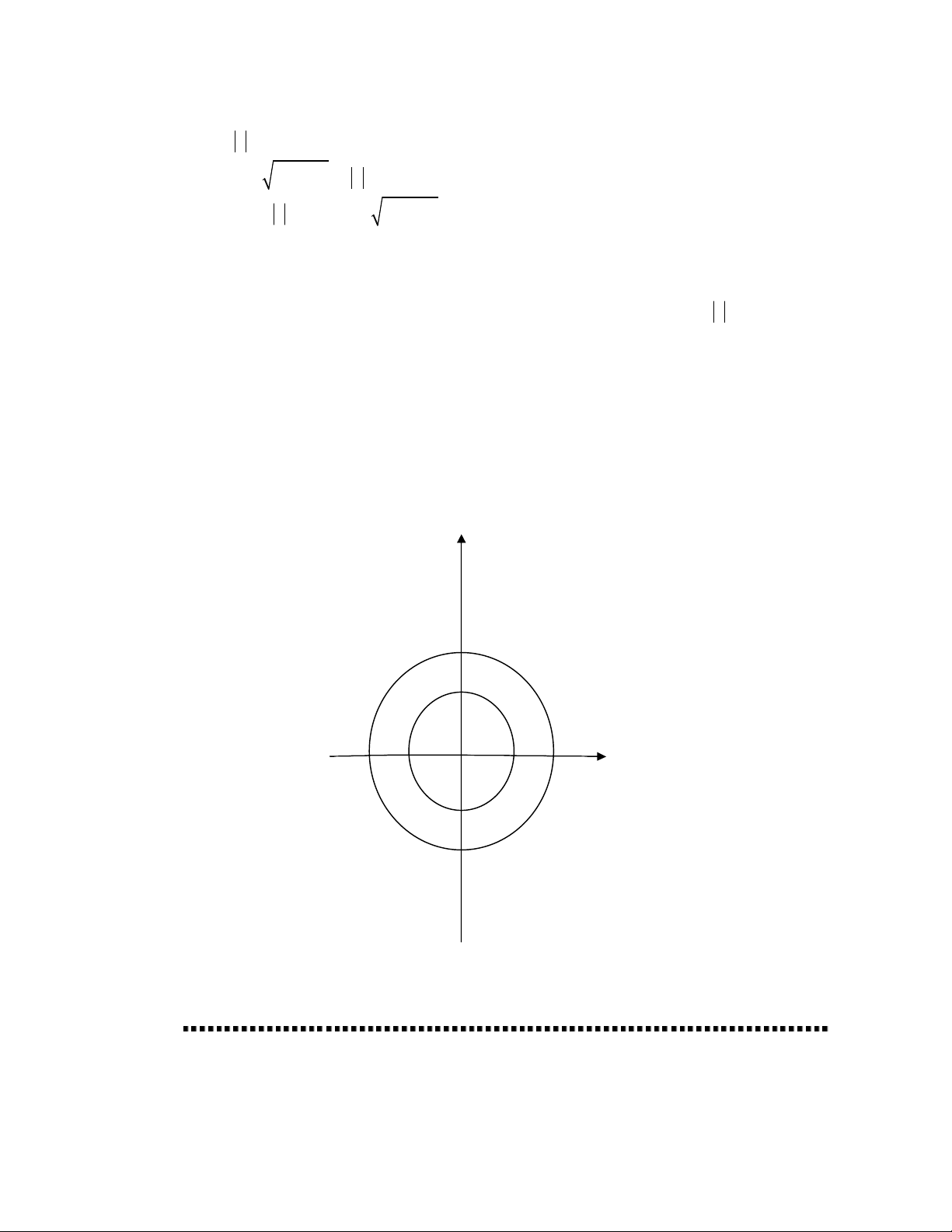
Do đó tập hợp những điểm biểu diễn số phức có độ lớn bằng 1 là đường tròn (0,1)
được biểu diễn như trên hình vẽ:
(y)
1
(x)
-1 0 1
-1
d)
1
< z 2
Ta có r =
2 2
a b
=
z
Suy ra:
1
< z 2
1<
2 2
a b
2
1 < a2 + b2 4
Tương tự như câu c ta có nhận xét:
Tập hợp những điểm biểu diễn số phức có độ lớn bằng 1 là đường tròn (0,1)
Tập hợp những điểm biểu diễn số phức có độ lớn bằng 2 là đường tròn (0,2)
Do đó tập hợp những điểm biểu diễn số phức có độ lớn thỏa mãn
1
< z 2 là phần
mặt phẳng bên trong giới hạn bởi 2 đường tròn (0,1) và (0,2) bao gồm cả những
điểm nằm trên đường tròn (0,2) như theo hình vẽ dưới đây:
(y)
2
1
(x)
-2 -1 0 1 2
-1
-2
Câu 3: Thực hiện các phép tính sau:
a) A = 2
3 2
i
i
f) F =
21
321
335
i
i
Giải:
a) A =
2
2
2 (3 2 )
2 6 7 2 4 7
3 2 3 2 3 2 9 4 13
i i
i i i i
i i i i
f) F =
21
321
335
i
i=
21
2
2
21
213
31313
121
313185
121
321335
i
i
ii
i
ii
=
21
31 i
Đặt A = -1 + i 3
F = A21
Viết A = -1 + i 3 dưới dạng lượng giác:
Modun: r =
2
231 =2
Argument:
1
cos 2
2
2
3
3
sin 2
k
Lấy giá trị chính
2
3
Suy ra dạng lượng giác của A là: A = 2
3
2
sin.
3
2
cos
i
F = A21 = 221.
21.2 21.2
cos .sin
3 3
i
= 221(1 + 0) = 221
Vậy F =
21
321
335
i
i= 221
Câu 5a: Giải các phương trình sau trên tập hợp số phức: -3z 2+ 2z – 1 = 0
Giải:
Ta có : '
= 12 – 3 = -2 = 2i2
Do đó phương trình đã cho có 2 nghiệm:
X1 =
3
21
3
21 2'' ii
a
b
X2 =
3
21
3
21 2''
ii
a
b