1/10
BÀI TẬP TOÁN CAO CẤP C2
Baøi 1.1 Thöïc hieän caùc pheùp toaùn sau
a)
1 3
6 5
0 0
2 3
2 11 5
7 3 2
b)
4 1 3 2
2
1
0
5
c)
5
3
2
1
1 4 9 3
d)
2 1 1
1 2 1
4
2
0
1 2
e)
1
2
3
;
223
012
;
410
112 CBA
. Tính (2A + 3B)C.
f) A =
1 1 0
0 1 1
1 0 1
; f(x) = 3x2 + 2x - 4. Tính f(A). g)
Ra
n
a
,
10
1
vaø n N.
h)
A ; B ; C ; D
0 1 2 1
0 1 1 2 1 0
2 1 3 1
0 1 2 1 0 1
3 1 0 2
.
Tính A - 2B + (3C – D)T
Tính (ATB)T – (2C)DT– 3I3
Baøi 1.2
a) Tính AB - BA biết A =
14
21
, B =
.
b) Tìm taát caû caùc ma traän caáp 2 giao hoaùn vôùi ma traän A =
10
12
Baøi 1.3 Cho caùc ma traän A =
522
221
311
, B =

, C =
 
a) Tính 5A -BC, (AB)C , (BC)TAT.
b) Tính f(A) bieát f(x) = 2x2 + 3x + 5.
Baøi 1.4 Cho ma traän A =

. Tìm ma traän nghòch ñaûo A-1 baèng phöông phaùp
Gauss- Jordan (phöômg phaùp bieán ñoåi sô caáp haøng ma traän).
2/10
Baøi 1.5 Cho ma traän A =


 
. Tìm ma traän nghòch ñaûo A-1 baèng phöông phaùp
phần bù đại số.
Baøi 1.6 Tìm ma traän X trong caùc tröôøng hôïp sau
a)
1 2
3 4
3 0
7 2
.X
; b)
X.3 2
2 1
1 2
1 1
;
c)
. .X
d)
2 1
1 2
1 1
1 1
1 1
1 1
. .X X
e)
X -
=3

f)
X
1 1 1
2 1 0
1 1 1
1 1 3
4 3 2
1 2 5
g) X
 





=


Baøi 1.7 Tính caùc ñònh thöùc sau
a)


; b)
; c)
;
d)
2 3 5 4
5 3 1 3
3 2 1 4
4 1 5 2

; e)
x y z
x z y
y y x
z z x
; f)
xxy xz
xy yyz
xz yz z
;
g)
a a a a
b b b b
ab a b ab a b
' '
' '
' ' ' '
h)
x x x
x x x
x x x
x x x
i)
a x x x x
x a x x x
x x a x x
x x x a x
x x x x a
.......
.......
........
................................
........
........
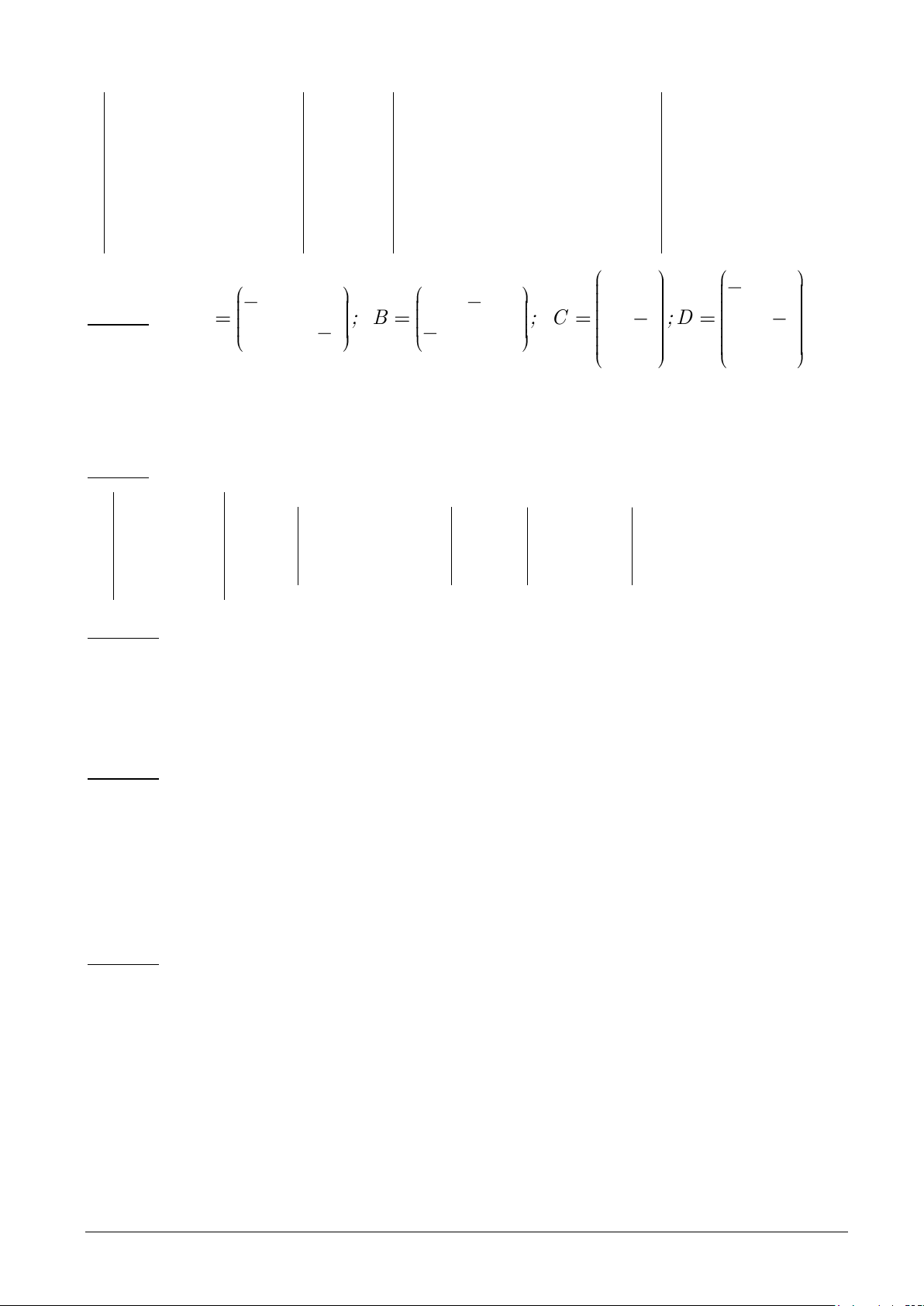
3/10
j)
.......
.......
........
......................................
............
........
n n
n n
n n
n
n
k)
nnnnn
nnnnn
nn
nn
nn
.......
1.......111
...............................
1.......333
1.......322
1.......321
Baøi 1.8 Cho
A ; B ; C ; D
1 0 1 1
1 0 1 1 1 0
0 1 1 1
0 1 1 1 0 1
1 1 0 1
.
a. Tính det([(A – B)T + (C – 2D)]A)
b. Tính det((ATB) + (3C)DT – I3)
Baøi 1.9 Giaûi caùc phöông trình, baát phöông trình sau
a)

 
x x x
=0; b)
x x x
x x x
x x x
=0 ; c)
2 2 1
1 1 2
5 3
x
x
> 0
Baøi 1.10 Chöùng minh raèng
a) Neáu A, B laø caùc ma traän vuoâng khaû nghòch caáp n vaø AB = BA thì A-1B-1 = B-1A-1
b) Neáu A1, A2,…, Ak laø caùc ma traän vuoâng khaû nghòch caáp n thì
(A1 . A2 …….Ak)-1 =
1
1
1
2
11
1
A.A......A.A kk
Baøi 1.11 Tìm haïng caùc ma traän sau
a)
1977
7115
4312
1531
b)
28112
71524
42312
c)
032
1050
713
541
420
d)
54471
13110
24121
01342
Baøi 1.12 Tìm haïng caùc ma traän sau (bieän luaän theo m)
a)
 m
b)

 





c)


m
d)
1 7 5 3 2
0 4 2 2 0
2 2 4 0 1
3 1 7 1 3
4/10
Baøi 1.13
a) Cho ma traän A =
m
m
m
. Tìm caùc giaù trò cuûa m ñeå r(A) = 2.
b) Cho ma traän A =
m
m m
m
. Tìm caùc giaù trò m ñeå r(A) < 3.
c) Cho ma traän A =


m
. Tìm caùc giaù trò m ñeå r(A) = 3.
Baøi 2.1 Giaûi caùc heä phöông trình sau ñaây bằng phương pháp Gauss
a)
x y z
x y z
x y z
  
 
; b)
x y z
x y z
x y z


 
;
c)
 

 
x y z
x y z
x y z


; d)
x y z
x y z
x y z
 
 
 



;
e)
2343
365
19252
1423
4321
4321
4321
4321
xxxx
xxxx
xxxx
xxxx
; f)
1255
232
132
123
zyx
tzyx
tzyx
tzyx
Baøi 2.2 Giaûi caùc heä phöông trình sau, chæ roõ nghieäm toång quaùt vaø heä nghieäm cô baûn (nếu
có)
a)
08723
0374
053
4321
4321
4321
xxxx
xxxx
xxxx
b)
025
0324
03
zyx
zyx
zyx
c)
x x x x
x x x x
x x x x
x x x x
d)
1 2 3
1 2 3
1 2 4
1 2 4
x 2x x 0
2x 3x 7x 0
x x 3x 0
5x x 2x 0
Baøi 2.3 Giaûi caùc heä phöông trình sau baèng phöông phaùp Cramer
a)
 

 
x y z
x y z
x y z


b)
x y z
x y z
x y z
 
 
 



5/10
c)
1 2 3
1 2 3
1 2 4
1 2 3
x 2x x 2
2x 3x 7x 1
x x 3x 6
5x x 2x 0
d)
x x x x
x x x x
x x x x
x x x x
 

  
  
Baøi 2.4 Giaûi vaø bieän luaän caùc heä phöông trình sau theo tham số m
a)
x y z
x y mz
xmy z


; b)
x y z
x y z m
x y m


;
c)
mx y z
xmy z m
x y mz m
; d)
x y m z m
m x y z
xmy z m


( )
( )
;
e)
x x x x
x x x x m
x x x x m
 
 
; f)

x x x x
x x x x
x x x x m
;
g)
x y z t
x y z t
x y z t
x y z m


 
 
; h)
x x x x
x x x x
x x x mx
x x x x
  
  
 
  
;
i)
x x x
x x x
x x x
x x x m

  


; j)
x x x mx m
x x x mx m
x x x mx m
x x x mx m
x x x mx m m
 
  
  
 
Baøi 2.5 Tìm ñieàu kieän cuûa tham soá m ñeå caùc heä phöông trình sau ñaây coù nghieäm
a)
mx y z m
x m y m z m
x y mz
( ) ( )
; b)
( )
m x my mz
xmy z m
x y mz
Baøi 2.6 Cho heä phöông trình
ax y z
ax y z
x y z b
 


vôùi a, b laø caùc tham soá.
a) Xaùc ñònh a, b ñeå heä treân laø heä Cramer, khi ñoù haõy tìm nghieäm cuûa heä theo a, b.
b) Tìm a, b ñeå heä treân voâ nghieäm.
c) Tìm a, b ñeå heä treân coù voâ soá nghieäm vaø tìm nghieäm toång quaùt cuûa heä .
Baøi 2.7 Tìm caùc ña thöùc baäc ba f(x) bieát
a) f(1) = 2; f(-1) = -4; f(2) = 8; f(-2) = -28.
b) Ñoà thò haøm soá y = f(x) ñi qua caùc ñieåm: (1;4), (3;32), (-3;-4), (2;11).