Đ I H C QU C GIA TP H CHÍ MINHẠ Ọ Ố Ồ
Đ I H C QU C GIA TP H CHÍ MINHẠ Ọ Ố Ồ
Đ I H C CÔNG NGH THÔNG TINẠ Ọ Ệ
1
N i dungộ
1. Gi i thi uớ ệ
2. Đ i s Booleạ ố
3. Bi u di n các hàm logic d i d ng chính ể ễ ướ ạ
quy
4. T i thi u hóa các hàm logicố ể
5. Các ph n t logic c b nầ ử ơ ả
6. Bài t pậ
Đại số bool 2
33
GII THIU
ỚỆ
GII THIU
ỚỆ
Trong đ i s tr u t ngạ ố ừ ượ , đ i s ạ ố
Boole là m t ộc u trúc đ i sấ ạ ố có các
tính ch t c b n c a c các phép toán ấ ơ ả ủ ả
trên t p h pậ ợ và các phép toán logic.
C th , các phép toán trên t p h p ụ ể ậ ợ
đ c quan tâm là ượ phép giao, phép h pợ
, phép bù; và các phép toán logic là Và
, Ho cặ, Không.
4
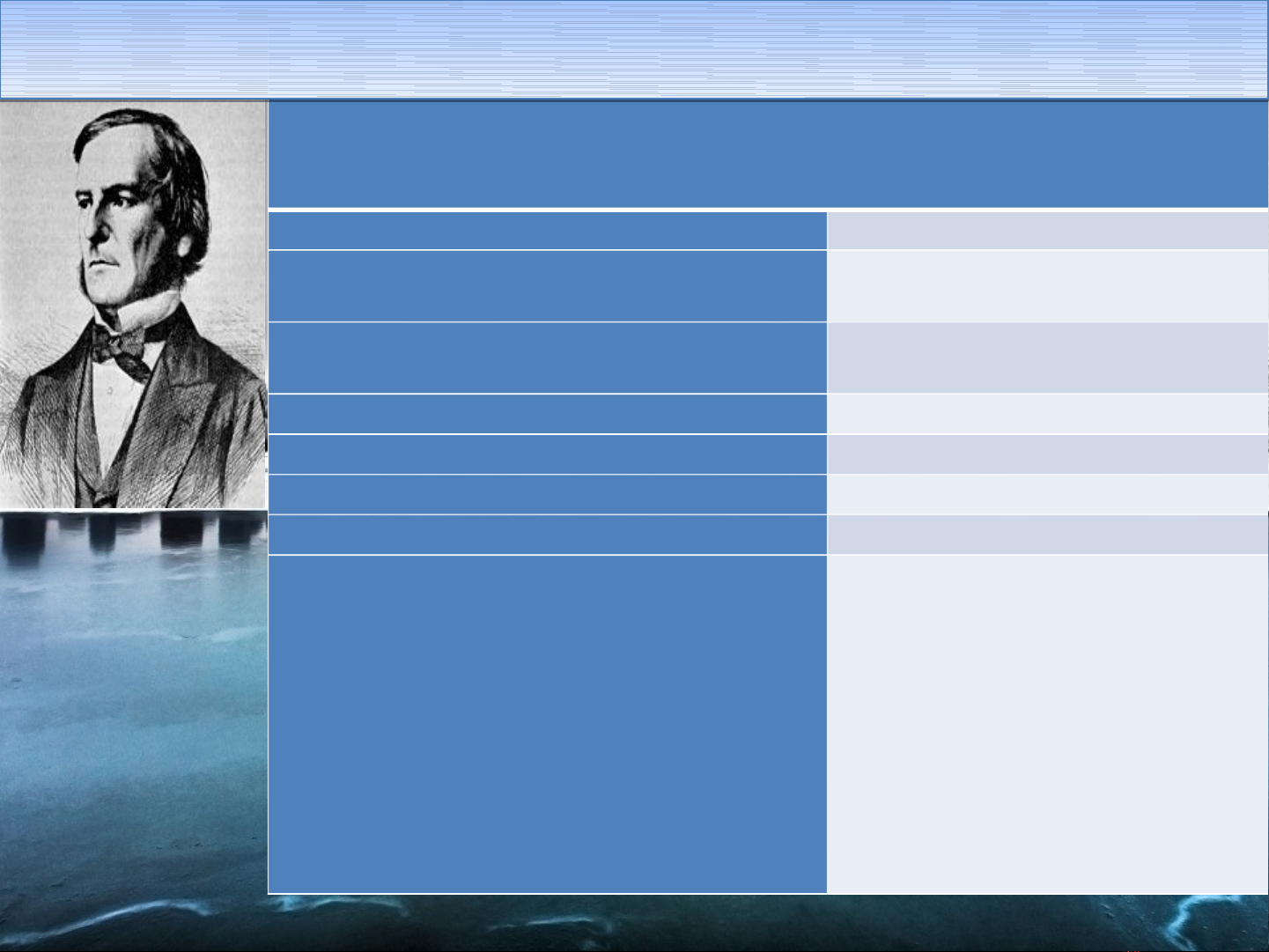
George Boole
Full name George Boole
Born 2 November 1815
Lincoln, Lincolnshire, England
Died 8 December 1864 (aged 49)
Ballintemple, County Cork, Ireland
Era 19th-century philosophy
Region Western Philosophy
School Mathematical foundations ofcomputer science
Main interests Mathematics, Logic, Philosophy of mathematics
Notable ideas Boolean algebra
N i dungộ
1. Gi i thi uớ ệ
2. Đ i s Booleạ ố
3. Bi u di n các hàm logic d i d ng chính ể ễ ướ ạ
quy
4. T i thi u hóa các hàm logicố ể
5. Các ph n t logic c b nầ ử ơ ả
6. Bài t pậ
Đại số bool 5