Giới thiệu tài liệu
Tài liệu này là đề thi cuối kỳ môn Xác suất và Thống kê (MT2013) dành cho sinh viên, bao gồm các câu hỏi đa dạng về các khái niệm cơ bản của môn học.
Đối tượng sử dụng
Sinh viên đại học chuyên ngành Toán học, Thống kê, hoặc các ngành có liên quan đang theo học môn Xác suất và Thống kê, cũng như các giảng viên và nhà nghiên cứu quan tâm đến đề thi mẫu.
Nội dung tóm tắt
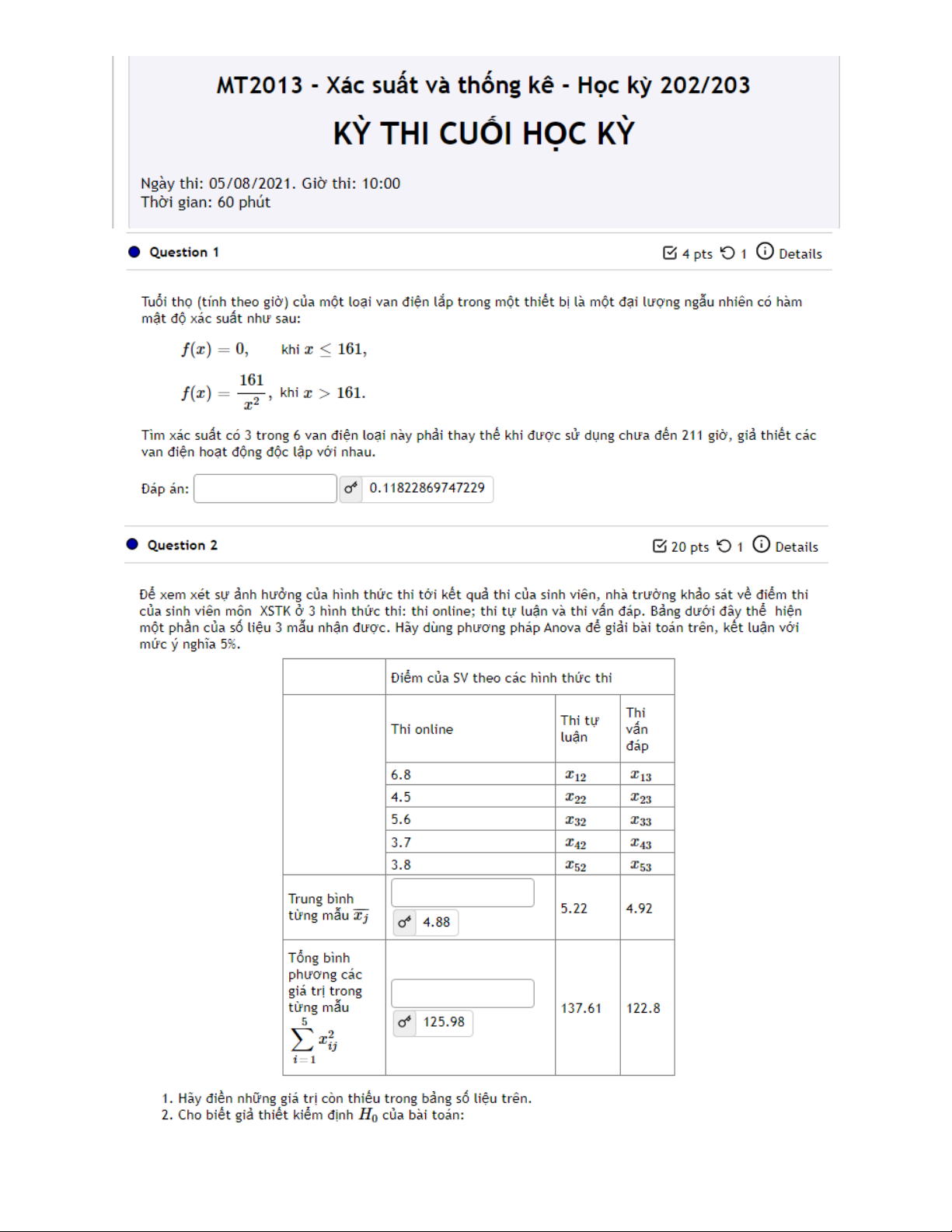
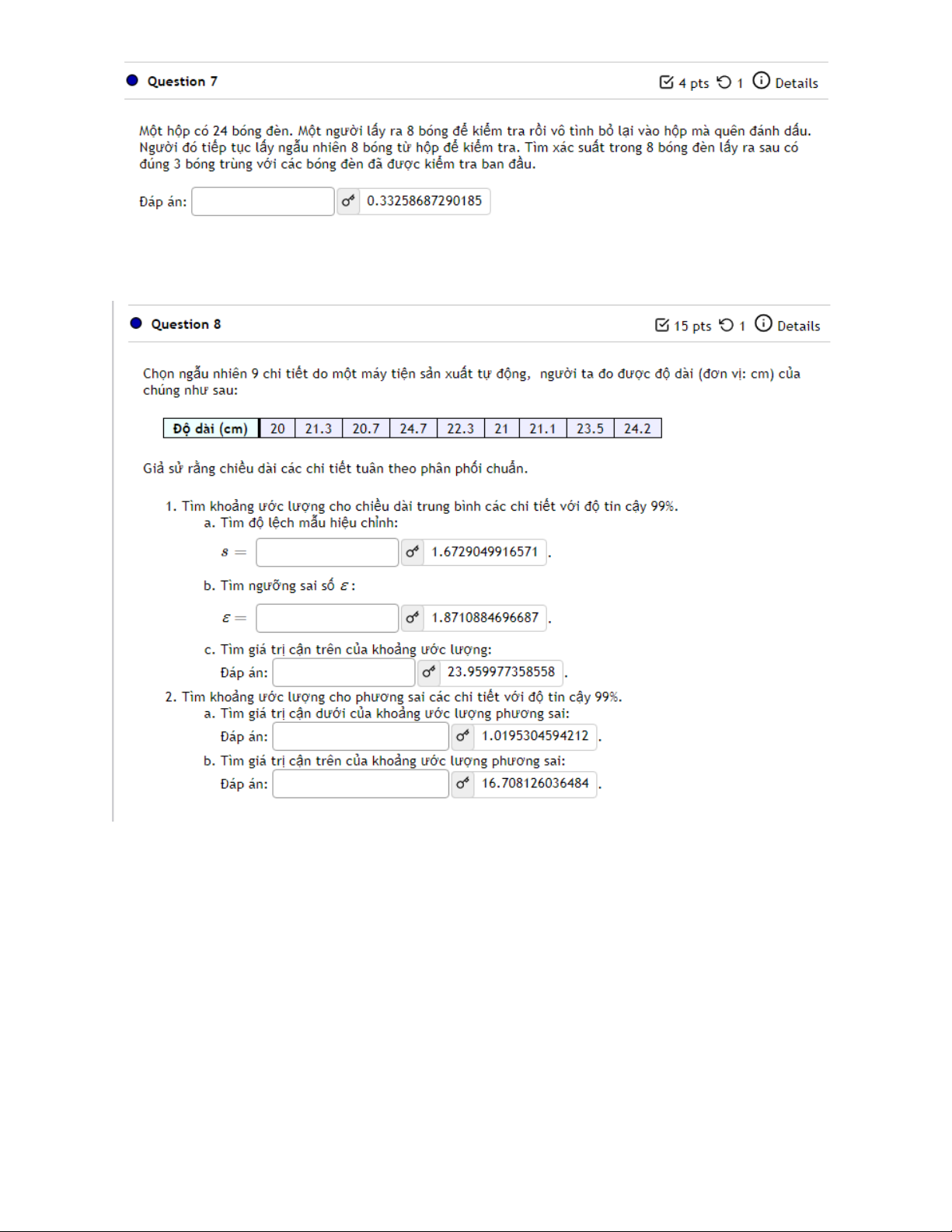
Tài liệu này trình bày đề thi cuối kỳ toàn diện cho môn Xác suất và Thống kê (MT2013), học kỳ 202/203. Đề thi được thiết kế trong 60 phút, bao gồm nhiều câu hỏi bao quát các chủ đề cốt lõi trong xác suất và thống kê. Các nội dung chính được đề cập bao gồm: Lý thuyết xác suất: Tính toán xác suất cho biến ngẫu nhiên liên tục với hàm mật độ xác suất cho trước, xác định xác suất cho các sự kiện độc lập, và áp dụng các khái niệm xác suất có điều kiện cùng định lý Bayes trong các tình huống thực tế như kiểm tra sản phẩm. Suy luận thống kê: Kiểm định giả thuyết: Thực hiện phân tích phương sai (ANOVA) để so sánh giá trị trung bình giữa nhiều nhóm (ví dụ: điểm thi theo hình thức thi), tiến hành kiểm định giả thuyết cho tỷ lệ tổng thể (ví dụ: tỷ lệ sinh viên thường xuyên đi xem phim), và so sánh giá trị trung bình của hai mẫu độc lập (ví dụ: số lần đi xem phim trung bình của nam và nữ sinh viên), kể cả trường hợp phương sai không bằng nhau. Khoảng tin cậy: Xây dựng khoảng tin cậy cho tỷ lệ, giá trị trung bình và phương sai của tổng thể dựa trên dữ liệu mẫu, đặc biệt đối với dữ liệu tuân theo phân phối chuẩn. Các phân phối: Làm việc với phân phối chuẩn (ví dụ: kiểm soát chất lượng sản phẩm), phân phối nhị thức (ví dụ: giới tính của trẻ em trong gia đình), và hiểu các thuộc tính của chúng như kỳ vọng và phương sai. Phân tích hồi quy: Áp dụng hồi quy tuyến tính để phân tích mối quan hệ giữa các biến (ví dụ: hàm lượng vitamin C/acid hữu cơ và thời gian bảo quản trong trái thanh long), bao gồm tính toán hệ số tương quan, các hệ số hồi quy và đưa ra dự đoán. Các câu hỏi đòi hỏi cả sự hiểu biết lý thuyết và khả năng ứng dụng thực tế các phương pháp thống kê, thường liên quan đến các phép tính số học và diễn giải kết quả.