107
Ch−¬ng 10. trao ®æi nhiÖt ®èi l−u
10.1. C¸c kh¸i niÖm c¬ b¶n
10.1.1. §Þnh nghÜa vµ ph©n lo¹i
Trao ®æi nhiÖt ®èi l−u, hay cßn gäi lµ táa nhiÖt, lµ hiÖn t−îng dÉn nhiÖt tõ
bÒ mÆt vËt r¾n vµo m«i tr−êng chuyÓn ®éng cña chÊt láng hay chÊt khÝ.
Tïy theo nguyªn nh©n g©y chuyÓn ®éng chÊt láng, táa nhiÖt ®−îc ph©n ra 2
lo¹i:
-Theo nhiÖt tù nhiªn lµ hiÖn t−îng dÉn nhiÖt vµo chÊt láng chuyÓn ®éng tù
nhiªn, lu«n x¶y ra trong tr−êng träng lùc khi nhiÖt ®é chÊt láng kh¸c nhiÖt ®é bÒ
mÆt.
- Táa nhiÖt c−ìng bøc lµ hiÖn t−îng dÉn nhiÖt vµo chÊt láng chuyÓn ®éng
c−ìng bøc do t¸c dông cña b¬m, qu¹t hoÆc m¸y nÐn.
10.1.2. C«ng thøc tÝnh nhiÖt c¬ b¶n.
Thùc nghiÖm cho hay l−îng nhiÖt Q trao ®æi b»ng ®èi l−u gi÷a mÆt F cã
nhiÖt ®é tw víi chÊt láng cã nhiÖt ®é tf lu«n tØ lÖ víi F vµ ∆t = tw - tf.
Do ®ã, nhiÖt l−îng Q ®−îc ®Ò nghÞ tÝnh theo 1 c«ng thøc quy −íc, ®−îc gäi
lµ c«ng thøc Newton, cã d¹ng sau:
hay],W[,tFQ ∆α=
]m/W[,tq 2
∆α=
10.1.3. HÖ sè táa nhiÖt α
HÖ sè α cña c«ng thøc Newton nãi trªn, ®−îc gäi lµ hÖ sè táa nhiÖt:
[
]
Km/W
t
q
tF
Q2
∆
=
∆
=α ,
HÖ sè α ®Æc tr−ng cho c−êng ®é táa nhiÖt, b»ng l−îng nhiÖt truyÒn tõ 1m2
bÒ mÆt ®Õn chÊt láng cã nhiÖt ®é kh¸c nhiÖt ®é bÒ mÆt 1 ®é
Gi¸ trÞ cña α ®−îc coi lµ Èn sè chÝnh cña bµi to¸n táa nhiÖt, phô thuéc vµo
c¸c th«ng sè kh¸c cña m«i tr−êng chÊt láng vµ bÒ mÆt, ®−îc x¸c ®Þnh chñ yÕu
b»ng c¸c c«ng thøc thùc nghiÖm.
10.1.4. C¸c th«ng sè ¶nh h−ëng tíi hÖ sè táa nhiÖt α
Táa nhiÖt lµ hiÖn t−îng dÉn nhiÖt tõ bÒ mÆt vµo m«i tr−êng chÊt láng
chuyÓn ®éng. Do ®ã, mäi th«ng sè ¶nh h−ëng ®Õn sù chuyÓn ®éng vµ dÉn nhiÖt
trong chÊt láng ®Òu ¶nh h−ëng tíi hÖ sè α. C¸c th«ng sè nµy th−êng ®−îc ph©n ra
4 lo¹i nh− sau:
* Th«ng sè h×nh häc:
M« t¶ vÞ trÝ, kÝch th−íc, h×nh d¹ng cña mÆt táa nhiÖt. Gi¸ trÞ cña th«ng sè
h×nh häc trong mçi c«ng thøc thùc nghiÖm ®−îc chän nh− mét kÝch th−íc nµo ®ã
108
cña mÆt F, ®−îc gäi lµ kÝch th−íc x¸c ®Þnh. Tïy theo vÞ trÝ vµ h×nh d¹ng cña mÆt
F, kÝch th−íc x¸c ®Þnh l cã thÓ chän lµ chiÒu cao h, chiÒu dµi l hoÆc ®−êng kÝnh
t−¬ng ®−¬ng u
f4
d=, víi f vµ u lµ diÖn tÝch vµ chu vi cña mÆt c¾t chøa chÊt láng.
* C¸c th«ng sè vËt lÝ cña chÊt láng:
C¸c th«ng sè vËt lÝ ¶nh h−ëng tíi α bao gåm:
- C¸c th«ng sè vËt lÝ ¶nh h−ëng tíi chuyÓn ®éng lµ: khèi l−îng riªng ρ
[kg/m3], hÖ sè në nhiÖt
[
]
1
0
K,
TV
V−
∆
=β , ®é nhít ®éng häc γ
[
]
sm /
2.
- C¸c th«ng sè ¶nh h−ëng tíi dÉn nhiÖt lµ: hÖ sè dÉn nhiÖt
[]
mK/Wλ, hÖ sè
khuyÕch t¸n nhiÖt
[
]
s/m
pC
a2
λ
=.
C¸c th«ng sè vËt lÝ nãi trªn ®Òu thay ®æi theo nhiÖt ®é chÊt láng. Trong mçi
thùc nghiÖm, ®Ó x¸c ®Þnh c¸c th«ng sè vËt lÝ, ng−êi ta quy ®Þnh 1 gi¸ trÞ nµo ®ã
cña nhiÖt ®é chÊt láng, ®−îc gäi lµ nhiÖt ®é x¸c ®Þnh. NhiÖt ®é x¸c ®Þnh cã thÓ µ
nhiÖt ®é tf, tW hay )tt(
2
1
twfm += , tïy m« h×nh cô thÓ, do nhµ thùc nghiÖm qui
®Þnh.
* Nguyªn nh©n g©y chuyÓn ®éng chÊt láng:
- ChuyÓn ®éng ®èi l−u tù nhiªn lu«n ph¸t sinh khi cã ®é chªnh träng l−îng
riªng gi÷a c¸c líp chÊt láng gÇn vµ xa v¸ch. §é chªnh träng l−îng riªng tØ lÖ víi
gia tèc träng lùc g[m/s2], víi hÖ sè në thÓ tÝch
[
]
1
K−
β vµ víi ®é chªnh nhiÖt ®é ∆t
gi÷a v¸ch vµ chÊt láng, tøc tØ lÖ víi tÝch gβ∆t,[m/s2].
- ChuyÔn ®éng c−ìng b−íc g©y ra bëi lùc c−ìng bøc cña b¬m qu¹t, ®−îc
®Æc tr−ng chñ yÕu b»ng tèc ®é ω [m/s] cña dßng chÊt láng. Khi chuyÓn ®éng
c−ìng bøc, nÕu g vµ ∆t kh¸c 0 th× lu«n kÌm theo theo ®èi l−u tù nhiªn.
* ChÕ ®é chuyÓn ®éng cña chÊt láng:
Khi ch¶y tÇng, c¸c phÇn tö chÊt láng chuyÓn ®éng song song mÆt v¸ch nÕu
sè α kh«ng lín. Khi t¨ng vËn tèc ω ®ñ lín, dßng ch¶y rèi sÏ xuÊt hiÖn. Lóc nµy
c¸c phÇn tö chÊt láng ph¸t sinh c¸c thµnh phÇn chuyÓn ®éng rèi lo¹n theo ph−¬ng
ngang, t¨ng c¬ héi va ch¹m mÆt v¸ch, khiÕn cho hÖ sè α t¨ng cao. chÕ ®é chuyÓn
®éng chÊt láng ®Æc tr−ng bëi c¸c th«ng sè l, γ vµ ω, th«ng qua gi¸ trÞ cña vËn tèc
kh«ng thø nguyªn:
Re=
⎪
⎩
⎪
⎨
⎧
≥
<≤
<
rèi ych¶:10Re
qu¸ ych¶:10Re2300
tÇng ych¶:2300Re
4
4
:
1
v
ω
®é (10-1)
Mét c¸ch tæng qu¸t, hÖ sè táa nhiÖt α phô thuéc vµo c¸c th«ng sè liªn quan
®Õn bµi to¸n táa nhiÖt, theo ph©n tÝch ®Þnh tÝnh nãi riªng trªn, sÏ cã d¹ng:
α = f (l, ρ, γ , a, λ, g, β, ∆t, ω ) (10-2)
109
10.2. ph−¬ng tr×nh tiªu chuÈn cña táa nhiÖt
ph−¬ng tr×nh tiÓu chuÈn cña táa nhiÖt lµ ph−¬ng tr×nh (10-2) ®−îc viÕt ë
d¹ng tiªu chuÈn, chØ chøa c¸c biÕn sè ®éc lËp kh«ng thø nguyªn. D¹ng tæ qu¸t cña
ph−¬ng tr×nh tiªu chuÈn cã thÓ t×m ®−îc b»ng ph−¬ng ph¸p biÕn ®æi ®ång d¹ng
hoÆc ph−¬ng ph¸p ph©n tÝch thø nguyªn.
10.2.1. Ph−¬ng ph¸p ph©n tÝch thø nguyªn
C¬ së cña ph−¬ng ph¸p ph©n tÝch thø nguyªn lµ nguyªn lÝ cho r»ng néi
dung cña ph−¬ng tr×nh m« t¶ mét hiÖn t−îng vËt lÝ sÏ kh«ng ®æi khi thay ®æi ®¬n
vÞ ®o c¸c ®¹i l−îng vËt lÝ chøa trong ph−¬ng tr×nh.
Môc ®Ých cña ph−¬ng ph¸p nµy lµ t×m c¸ch thay ®æi ®¬n vÞ ®o thÝch hîp ®Ó
khö c¸c biÕn phôc thuéc, ®−a ph−¬ng tr×nh (10 -2) vÒ d¹ng tiªu chuÈn, chØ chøa
c¸c biÕn ®éc lËp kh«ng thø nguyªn.
10.2.2. D¹ng tæng qu¸t cña ph−¬ng tr×nh tiªu chuÈn táa nhiÖt
Ph©n tÝch thø nguyªn cña c¸c ®¹i l−îng vËt lÝ trong ph−¬ng tr×nh (10-2) ®Ó
t×m ®¬n vÞ ®o c¬ b¶n:
[] [ ] [ ]
[
]
[
]
[
]
[
]
[
][]
[
]
;s/ma;s/m;s/m;m/kg;m1 223 ==ω=γ=ρ=
[]
[
]
[]
[
]
[
]
[
]
[
]
[
]
Ks/kgKm/W¦;Ks/kgmmK/W¦;s/mtg 3222 ==α==λ=∆β
§¬n vÞ ®o chung cho c¸c ®¹i l−îng, hay ®¬n vÞ ®o c¬ b¶n, lµ hÖ 4 ®¬n vÞ
sau:
([kg]; [m]; [s]; [K])
Khi ®o b»ng hÖ ®¬n vÞ c¬ b¶n míi (G[kg], M[m], S[s], D[K]), víi G, M, S,
D lµ c¸c hÖ sè tØ lÖ sÏ ®−îc chän, th× ph−¬ng tr×nh (10-2) sÏ cã d¹ng:
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛ω∆βλγρ=α S
M
,tg
S
M
,a
S
M
,
DS
GM
,
S
M
,
M
G
,Mlf
DS
G
2
2
3
2
32 (10-3)
§Ó khö c¸c biÕn phô thuéc, cÇn chän 4 h»ng sè G, M, S, D sao cho 4 ®¹i
l−îng ®Çu trong ph−¬ng tr×nh (10-3) b»ng 1:
⎪
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎪
⎬
⎫
=λ
=
=ρ
=
1
DS
GM
1v
S
M
1
M
G
11M
3
2
3
Tøc lµ
⎪
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎪
⎨
⎧
ρ
λ
=
=
ρ
=
=
3
2
2
3
v
1
D
1
v
S
1
1
G
1
1
M
Thay gi¸ trÞ c¸c hÖ t×m ®−îc vµo ph−¬ng tr×nh (10-3) sÏ cã:
Re), Gr, f(Pr, Nuhay
v
,
v
lg
,
a
v
1,1,1,1,f
l
2
3
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=ωl
β∆t
λ
α (10-4)
110
Trong ®ã:
- Nu = λ
αllµ hÖ sè táa nhiÖt kh«ng thø nguyªn ch−a biÕt, ®−îc gäi lµ tiªu
chuÈn Nusselt, ®Æc tr−ng cho c−êng ®é táa nhiÖt.
a
Pr
γ
=− lµ ®é nhít kh«ng thø nguyªn, cho tr−íc trong ®iÒu kiÖn vËt lÝ,
®−îc gäi lµ tiªu chuÈn Prandtl, ®Æc tr−ng cho tÝnh chÊt vËt lÝ cña chÊt láng.
v
l
Re ω
=− lµ vËn tèc kh«ng thø nguyªn, ®−îc gäi lµ tiªu chuÈn Reynolds,
®Æc tr−ng cho chÕ ®é chuyÓn ®éng. Trong táa nhiÖt c−ìng bøc Re lµ tiªu chuÈn
x¸c ®Þnh. Trong táa nhiÖt tù nhiªn, Re lµ tiªu chuÈn ch−a x¸c ®Þnh phô thuéc vµo
Gr vµ Pr.
2
3
y
tlg
Gr ∆β
=− lµ lùc n©ng kh«ng thø nguyªn, cho tr−íc theo ®iÒu kiÖn ®¬n
trÞ, ®−îc gäi lµ tiªu chuÈn Grashof, ®Æc tr−ng cho c−êng ®é ®èi l−u tù nhiªn.
10.2.3. C¸c d¹ng ®Æc biÖt cña ph−¬ng tr×nh tiªu chuÈn táa nhiÖt
Khi ®èi l−u tù nhiªn ®¬n thuÇn, Re lµ Ên sè phô thuéc Gr vµ Pr, nªn ph−¬ng
tr×nh (10-4) sÏ cã d¹ng:
Nu=f (Gr,Pr).
Khi chuyÓn ®éng c−ìng bøc m¹nh, cã thÓ coi Gr = const, lóc ®ã ph−¬ng
tr×nh (10- 4) cã d¹ng:
Nu = f (Re,Pr).
Khi m«i tr−êng lµ hÊt khÝ, cã Pr = const, ph−¬ng tr×nh (10-4) cã d¹ng:
Nu=f(Gr,Re).
Khi chÊt khÝ ®èi l−u tù nhiªn th× Nu = F(Gr), khi chÊt khÝ chuyÓn ®éng
c−ìng bøc m¹nh th× Nu = f(Re).
10.3. c¸ch x¸c ®Þnh c«ng thøc thùc nghiÖm
10.3.1. C¸c b−íc thùc nghiÖm
Khi cÇn thiÕt lËp c«ng thøc tÝnh α cho 1 hiÖn t−îng táa nhiÖt, ng−êi ta tiÕn
hµnh c¸c b−íc nh− sau:
1. LËp m« h×nh thÝ nghiÖm ®ång d¹ng víi hiÖn t−îng táa nhiÖt ®ang xÐt
2. §o c¸c gi¸ trÞ cña tÊt c¶ c¸c ®¹i l−îng t¹i c¸c chÕ ®é cÇn kh¶o s¸t.
3. lËp b¶ng tÝnh c¸c gi¸ trÞ t−¬ng øng cña c¸c tiªu chuÈn Re, Gr, Pr, Nu
theo c¸c sè liÖu thu ®−îc t¹i k ®iÓm ®o kh¸c nhau.
4. lËp c«ng thøc thùc nghiÖm Nu = f (Gr,Re,Pr) theo b¶ng gi¸ trÞ c¸c tiªu
chuÈn nãi trªn b»ng ph−¬ng ph¸p ®å thÞ.
10.3.2. Ph−¬ng ph¸p ®å thÞ t×m d¹ng ph−¬ng tr×nh tiªu chuÈn
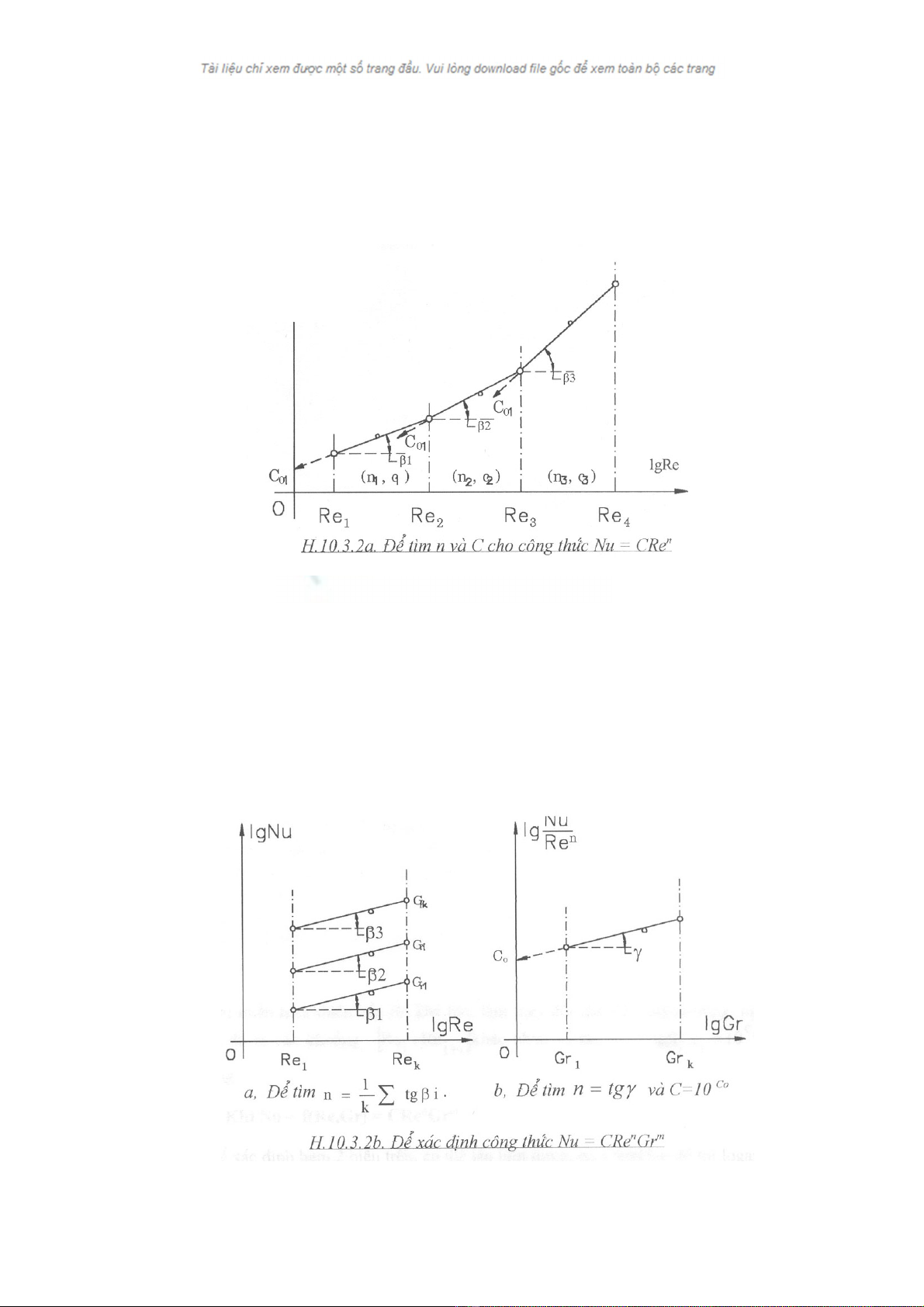
111
Tõ b¶ng sè liÖu (Nu, Re, Gr. Pr) ng−êi ta cã thÓ t×m c«ng thøc rhùc nghiÖm
ë d¹ng Nu = CRenGrmPrp b»ng c¸ch lÇn l−ît x¸c ®Þnh c¸c sè mò n, m, p vµ h»ng
sè C trªn c¸c ®å thÞ logarit.
10.3.2.1. Khi Nu = f(Re) = CRen
Trªn ®å thÞ (lgNu, lgRe) ph−¬ng tr×nh trªn cã d¹ng ®−êng th¼ng lgNu =
nlgRe + lgC, víi n, C ®−îc x¸c ®Þnh nh− sau:
- BiÔu diÔn c¸c ®iÓm thùc nghiÖm trªn ®å thÞ (lgNu,lgRe)
- X¸c ®Þnh ®−êng th¼ng ®i qua tËp ®iÓm thùc nghiÖm nãi trªn theo ph−¬ng
ph¸p b×nh ph−¬ng nhá nhÊt.
- T×m gãc nghiªng β cña ®−êng th¼ng vµ giao ®iÓm C0 = lgC víi trôc lgNu,
nhê ®ã t×m ®−îc n = tgβ vµ C = 10C0
Khi miÒn biÕn thiªn cña Re kh¸ lín, lµm thay ®æi chÕ ®é chuyÓn ®éng
ng−êi ta chia miÒn ®ã ra c¸c kho¶ng
⎣
⎦
1
ReRe +
÷
ii kh¸c nhau vµ t×m ni = tgβi, Ci =
10C0i cho mçi kho¶ng.