
BÁO CÁO K T QU Ế Ả
NGHIÊN C U, NG D NG SÁNG KI NỨ Ứ Ụ Ế
1. L i gi i thi uờ ớ ệ
V t lý là m t môn h c g n li n v i các hi n t ng trong đi s ng và kĩậ ộ ọ ắ ề ớ ệ ượ ờ ố
thu t h ng ngày. Nó là môn h c khó và tr u t ng, c s c a nó là toán h c.ậ ằ ọ ừ ượ ơ ở ủ ọ
Bài t p v t lý r t đa d ng và phong phú.ậ ậ ấ ạ
B i d ng h c sinh gi i nói chung và b i d ng h c sinh gi i môn v tồ ưỡ ọ ỏ ồ ưỡ ọ ỏ ậ
lí nói riêng cho các k thi tuy n h c sinh gi i là v n đ luôn đc các c pỳ ể ọ ỏ ấ ề ượ ấ
qu n lý, các giáo viên tr c ti p gi ng d y quan tâm, trăn tr . Đây là công vi cả ự ế ả ạ ở ệ
hàng năm, khó khăn th ng nhi u h n thu n l i, nh ng r t có ý nghĩa đi v iườ ề ơ ậ ợ ư ấ ố ớ
các tr ng THPT. K t qu thi h c sinh gi i s l ng và ch t l ng là m tườ ế ả ọ ỏ ố ượ ấ ượ ộ
trong các tiêu chí quan tr ng, ph n ánh năng l c, ch t l ng d y và h c c aọ ả ự ấ ượ ạ ọ ủ
các tr ng, c a giáo viên và h c sinh.ườ ủ ọ
Th c tr ng trình đ nh n th c c a h c sinh THPT ch a cao, đc bi t làự ạ ộ ậ ứ ủ ọ ư ặ ệ
đi v i h c sinh vùng nông thôn, trung du phân ph i th i gian cho h c t p cònố ớ ọ ố ờ ọ ậ
ít so v i l ng ki n th c c a SGK và thi u th n sách tham kh o nên vi cớ ượ ế ứ ủ ế ố ả ệ
nh n d ng và phân lo i, t ng h p các d ng bài toán đ xác đnh đc cáchậ ạ ạ ổ ợ ạ ể ị ượ
gi i c a bài toán là h t s c khó khăn đi v i ph n l n h c sinh.ả ủ ế ứ ố ớ ầ ớ ọ
Trong quá trình d y h c ạ ọ chuyên đ ềvà b i d ng HSG v t lý 11ồ ưỡ ậ , 12 khi
d y ạph n “C m ng đi n t ”,ầ ả ứ ệ ừ tôi nh n th y các em đu g p khó khăn trongậ ấ ề ặ
khi làm bài t p ph n này. Đa s các em ch có th làm đc các bài toán ậ ầ ố ỉ ể ượ cơ
b n, mang tính ch t v n d ng công th c tr ít khi hi u rõ đc hi n t ng,ả ấ ậ ụ ứ ứ ể ượ ệ ượ
b n ch t và làm đc nh ng bài toán mang tích ch t ph c t p.ả ấ ượ ữ ấ ứ ạ
Trong quá trình d y h c và b i d ng h c sinh khá gi i, đ gi i đcạ ọ ồ ưỡ ọ ỏ ể ả ượ
các bài toán v ph n này đòi h i các em ph i có tính v n d ng caoề ầ ỏ ả ậ ụ . Chính vì
th , ng i giáo viên ph i làm th nào đ tìm ra ph ng pháp, phân lo i bàiế ườ ả ế ể ươ ạ
t p t t nh t nh m t o cho h c sinh ni m say mê yêu thích môn h c này vàậ ố ấ ằ ạ ọ ề ọ
giúp h c sinh vi c phân lo i các d ng bài t p và h ng d n cách gi i đnọ ệ ạ ạ ậ ướ ẫ ả ơ
gi n và nhanh nh t, chính xác nh t là r t c n thi t cho hình th c thi ch n h cả ấ ấ ấ ầ ế ứ ọ ọ
sinh gi i V t lí hi n nay. Vi c làm này r t có l i cho h c sinh trong th i gianỏ ậ ệ ệ ấ ợ ọ ờ
ng n n m đc các d ng bài t p, n m đc ph ng pháp gi i và t đó cóắ ắ ượ ạ ậ ắ ượ ươ ả ừ
1

th phát tri n h ng tìm tòi l i gi i m i cho các d ng bài t ng t .ể ể ướ ờ ả ớ ạ ươ ự Đ gi iể ả
quy t v n đ trên tôi b c vào nghiên c u đ tàiế ấ ề ướ ứ ề “CHUYÊN Đ C M NGỀ Ả Ứ
ĐI N T B I D NG H C SINH GI I L P 11, 12”.Ệ Ừ Ồ ƯỠ Ọ Ỏ Ớ
2. Tên sáng ki n:ế “CHUYÊN Đ C M NG ĐI N T B I D NG Ề Ả Ứ Ệ Ừ Ồ ƯỠ
H C SINH GI I L P 11, 12”.Ọ Ỏ Ớ
3. Tác gi sáng ki n:ả ế
- H và tên: ọNguy n Văn Tu n.ễ ấ
- Đa ch tác gi sáng ki n: ị ỉ ả ế Tr ng THPT Đng Đu.ườ ồ ậ
- S đi n tho i: ố ệ ạ 0965.761.978. E_mail: nguyentuan.ly@gmail.com.
4. Ch đu t t o ra sáng ki n: Nguy n Văn Tu nủ ầ ư ạ ế ễ ấ
5. Lĩnh v c áp d ng sáng ki n: ự ụ ế Ôn thi h c sinh gi i V t lý l p 11, 12 c p ọ ỏ ậ ớ ấ
t nh.ỉ
6. Ngày sáng ki n đc áp d ng l n đu: ế ượ ụ ầ ầ 15/8/2019
7. Mô t b n ch t c a sáng ki n:ả ả ấ ủ ế
I - M T S KI N TH C V LÝ THUY TỘ Ố Ế Ứ Ề Ế
1. T thông qua di n tích S đt trong t tr ng đu Φừ ệ ặ ừ ườ ề
B
đc tính b iượ ở
công th cứ
cos..SB
Trong đó:
B là c m ng t c a t tr ng (T);ả ứ ừ ủ ừ ườ
S là ti t di n khung dây (mế ệ 2);
nB;
là góc h p b i các đng s c t và pháp tuy n c aợ ở ườ ứ ừ ế ủ
m t ph ng khung dây;ặ ẳ
Φ là t thông (Wb).ừ
2. Hi n t ng c m ng đi n tệ ượ ả ứ ệ ừ
2

- Đi u ki n: Khi có ề ệ s bi n thiên t thôngự ế ừ qua di n tích gi i h n b i m tệ ớ ạ ở ộ
m ch đi n kínạ ệ thì trong m ch xu t hi n dòng đi n c m ng.ạ ấ ệ ệ ả ứ
- Đnh lu t Len-x : Dòng đi n c m ng có chi u sao cho t tr ng do nó sinhị ậ ơ ệ ả ứ ề ừ ườ
ra ch ng l i s bi n thiên c a t thông sinh ra nó.ố ạ ự ế ủ ừ
3. Đnh lu t Faraday v c m ng đi n tị ậ ề ả ứ ệ ừ
- Đ l n c a su t đi n đng c m ng trong m ch đi n t l thu n v i t cộ ớ ủ ấ ệ ộ ả ứ ạ ệ ỷ ệ ậ ớ ố
đ bi n thiên c a t thông qua m ch.ộ ế ủ ừ ạ
- Bi u th c: ể ứ
t
ec
Trong đó:
Δ: là đ bi n thiên t thông trong th i gian Δt;Φộ ế ừ ờ
ec: là su t đi n đng c m ng c a khung dây.ấ ệ ộ ả ứ ủ
4. Su t đi n đng c m ng xu t hi n trên đo n dây chuy n đng trongấ ệ ộ ả ứ ấ ệ ạ ể ộ
t tr ng đuừ ườ ề
Ec = Bl.v.sinα
Trong đó:
B là c m ng t c a t tr ng đu (T);ả ứ ừ ủ ừ ườ ề
l là chi u dài c a đo n dây (m);ề ủ ạ
v là t c đ chuy n đng c a đo n dây (m/s);ố ộ ể ộ ủ ạ
vB;
.
- Quy t c bàn tay ph i: Đt bàn tay ph i h ng các đng s c t , ngón cáiắ ả ặ ả ứ ườ ứ ừ
choãi ra 90o h ng theo chi u chuy n đng c a đo n dây, khi đó đo n dâyướ ề ể ộ ủ ạ ạ
d n đóng vai trò nh m t ngu n đi n, chi u t c tay đn b n ngón tay chẫ ư ộ ồ ệ ề ừ ổ ế ố ỉ
chi u t c c âm sang c c d ng c a ngu n đi n đó.ề ừ ự ự ươ ủ ồ ệ
5. T c mự ả
- Đ t c m c a m t ng dây: ộ ự ả ủ ộ ố
S
l
N
I
L
2
7.10.4
3

Trong đó:
I là c ng đ dòng đi n ch y trong ng dây (A).ườ ộ ệ ạ ố
là t thông qua ti t di n ng dây (Wb).Φừ ế ệ ố
L là h s t c m (H).ệ ố ự ả
- Su t đi n đng t c m: ấ ệ ộ ự ả
t
LEtc
.
- Năng l ng t tr ng c a ng dây: ượ ừ ườ ủ ố
2
.
2
1ILW
II – PHÂN LO I BÀI T P TRONG NGHIÊN C U, NG D NG SÁNGẠ Ậ Ứ Ứ Ụ
KI NẾ
1. Bài t p xác đnh chi u c a dòng đi n c m ngậ ị ề ủ ệ ả ứ
1.1. Ph ng pháp gi i bài t p:ươ ả ậ
* Áp d ng đnh lu t Len-x v chi u dòng đi n c m ng:ụ ị ậ ơ ề ề ệ ả ứ
G i: ọ
B
là c m ng t c a t tr ng ban đu;ả ứ ừ ủ ừ ườ ầ
c
B
là c m ng t c a t tr ng do dòng đi n c m ng sinh ra.ả ứ ừ ủ ừ ườ ệ ả ứ
-N u ế
tăng thì c m ng t ả ứ ừ
c
B
ng c chi u v i chi u c a c m ng tượ ề ớ ề ủ ả ứ ừ
B
.
-N u ế
gi m thì c m ng t ả ả ứ ừ
c
B
cùng chi u v i chi u c a c m ng tề ớ ề ủ ả ứ ừ
B
.
* Các b c xác đnh chi u dòng đi n c m ng:ướ ị ề ệ ả ứ
- Xác đnh chi u c a t tr ng ban đu ị ề ủ ừ ườ ầ
B
.
- Xét t thông ừ
(s đng s c t ) qua ti t di n khung dây tăng hay gi m.ố ườ ứ ừ ế ệ ả
- D a vào đnh lu t Len-x đ xác đnh chi u c a ự ị ậ ơ ể ị ề ủ
c
B
.
- Áp d ng quy t c đinh c đ xác đnh chi u c a dòng đi n c m ng.ụ ắ ố ể ị ề ủ ệ ả ứ
1.2. Ví d :ụ
4
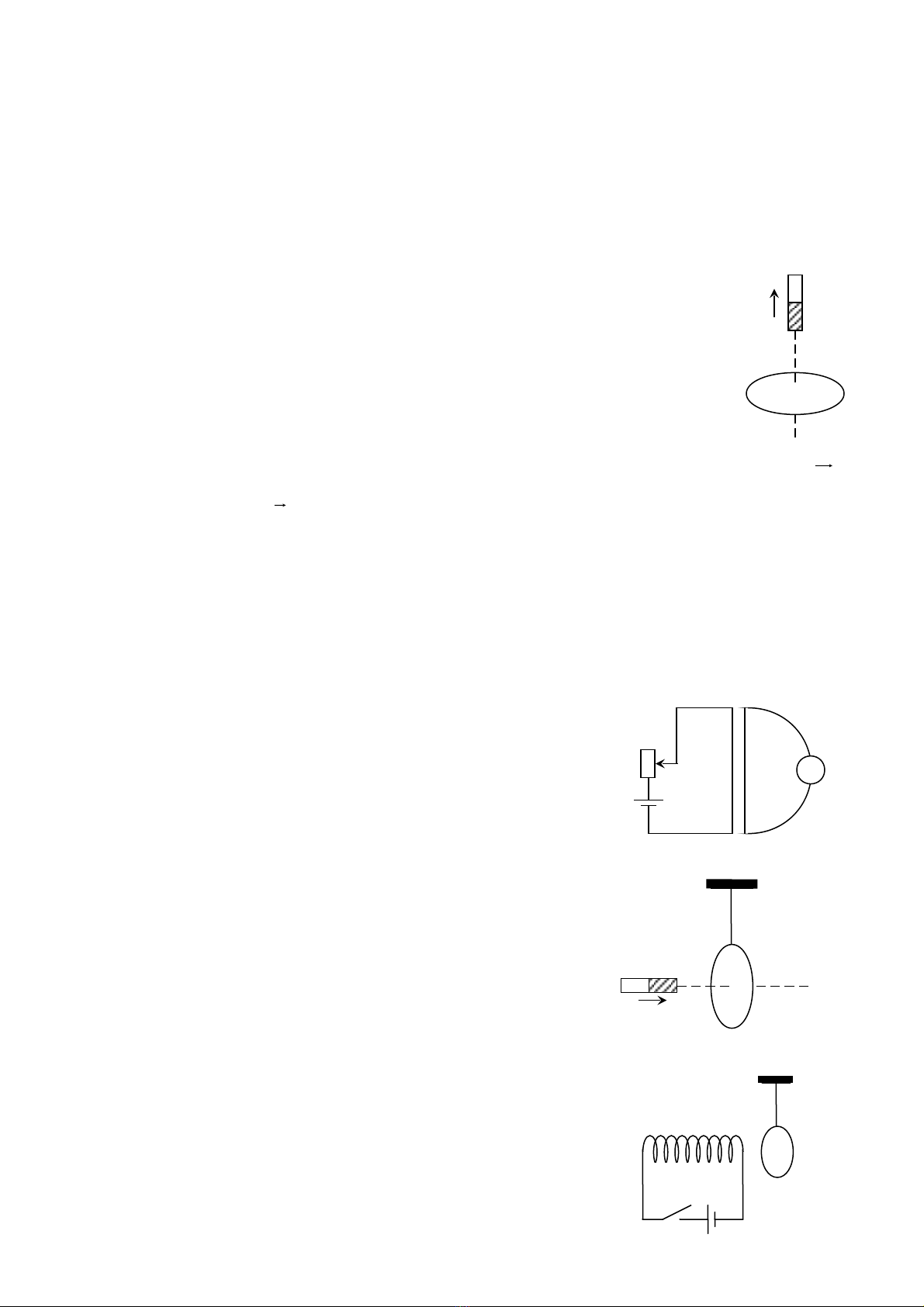
Ví d 1:ụ Cho h th ng nh hình v : Nam châm chuy n đng lên phía trênệ ố ư ẽ ể ộ
theo ph ng th ng đng, xác đnh chi u dòng đi n c m ng trong vòng dây.ươ ẳ ứ ị ề ệ ả ứ
D i tác d ng c a l c t , vòng dây có th chuy n đng theo chi u nào?ướ ụ ủ ự ừ ể ể ộ ề
Gi i:ả
- T tr ng do nam châm sinh ra đi qua vòng dây s t o ra m t từ ườ ẽ ạ ộ ừ
thông qua vòng dây.
- Khi nam châm ra xa vòng dây, s đng s c qua ti t di n vòngố ườ ứ ế ệ
dây là gi m. Do đó, t thông qua vòng dây có đ l n gi m d n vàả ừ ộ ớ ả ầ
trong vòng dây xu t hi n dòng đi n c m ng Iấ ệ ệ ả ứ c.
- Áp d ng đnh lu t Len-x ta th y: Iụ ị ậ ơ ấ c sinh ra t tr ng có c m ng t ừ ườ ả ứ ừ
c
B
cùng chi u v i ề ớ
B
.
- Theo quy t c đinh c, ta suy ra đòng đi n Iắ ố ệ c có chi u nh hình v .ề ư ẽ
- Dòng đi n c m ng Ic khi n vòng dây có tác d ng nh m t nam châm màệ ả ứ ế ụ ư ộ
m t trên là m t Nam, m t d i là m t B c. Do đó, vòng dây b nam châm hút.ặ ặ ặ ướ ặ ắ ị
V y vòng dây có th chuy n đng lên phía trên.ậ ể ể ộ
1.3. Bài t p c ng c :ậ ủ ố
Bài 1. M t thí nghi m đc b trí nh hình v . ộ ệ ượ ố ư ẽ
Hãy xác đnh chi u dòng đi n c m ng trong m ch C ị ề ệ ả ứ ạ
khi con ch y bi n tr đi xu ng.ạ ế ở ố
Bài 2. M t nam châm đa l i g n vòng dây nh hìnhộ ư ạ ầ ư
v . H i dòng đi n c m ng trong vòng dây có chi uẽ ỏ ệ ả ứ ề
nh th nào và vòng dây s chuy n đng v phíaư ế ẽ ể ộ ề
nào?
Bài 3. M t vòng dây kim lo i treo trên s i dây m nhộ ạ ợ ả
song song v i m t c t c a m t cu n dây. Cu n dâyớ ặ ắ ủ ộ ộ ộ
5
S N
K
R
MP
N Q
AC
G






















