Robot c«ng nghiÖp 33
VÝ dô sau ®©y tr×nh bµy chi tiÕt cña c¸c b−íc khi thiÕt lËp hÖ ph−¬ng tr×nh ®éng häc
cña robot :
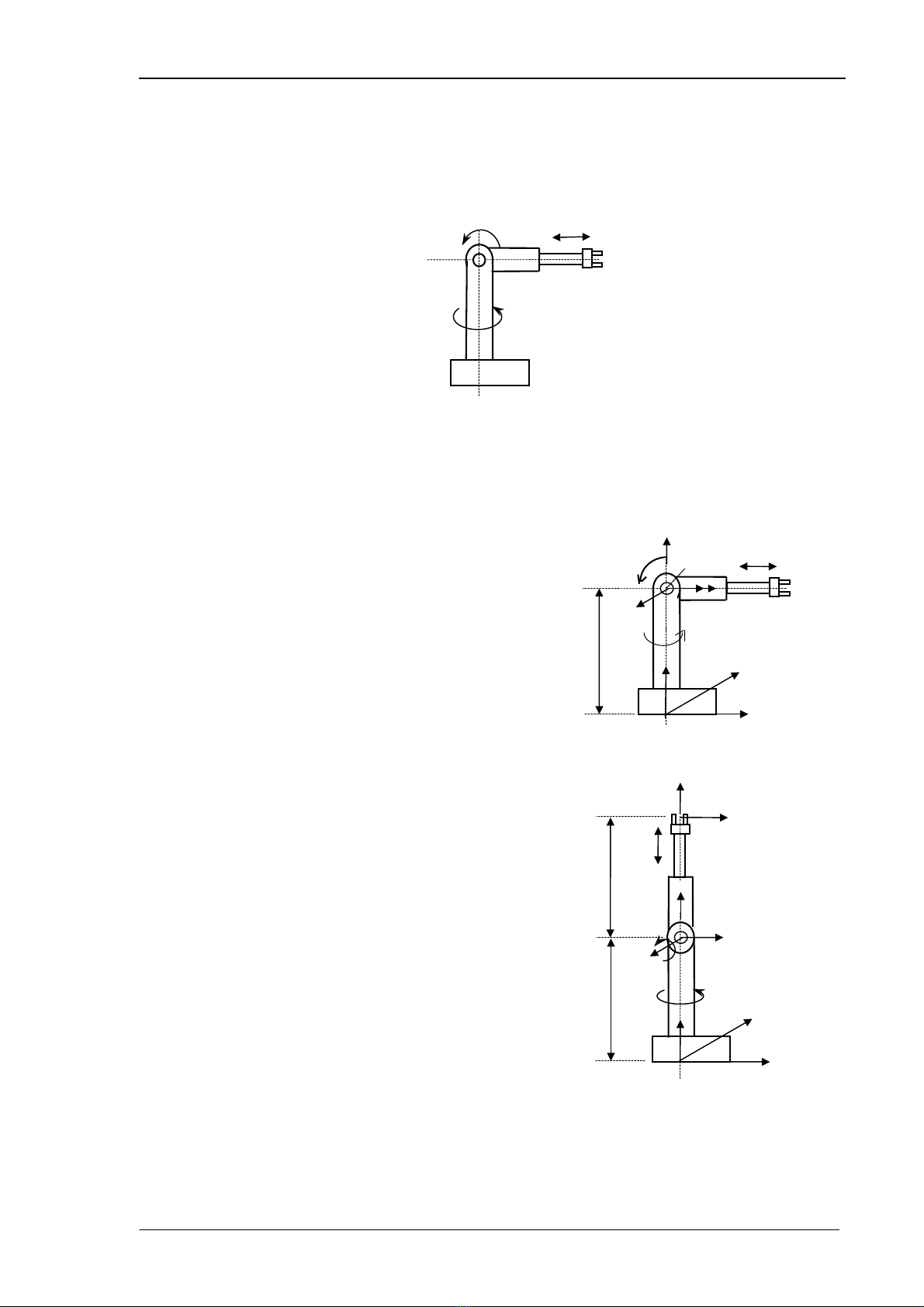
Cho mét robot cã ba kh©u, cÊu h×nh RRT nh− h×nh 3.11. H·y thiÕt lËp hÖ ph−¬ng tr×nh
®éng häc cña robot.
1. G¾n hÖ to¹ ®é lªn c¸c kh©u :
Ta gi¶ ®Þnh vÞ trÝ ban ®Çu vµ chän gèc to¹ ®é O0 cña robot nh− h×nh 3.12. C¸c trôc z ®Æt
cïng ph−¬ng víi c¸c trôc khíp.
Ta thÊy trôc z1 ®· quay t−¬ng ®èi mét
gãc 900 so víi trôc z0, ®©y chÝnh lµ phÐp quay
quanh trôc x0 mét gãc α1 (phÐp biÕn ®æi
Rot(x0,α1) trong biÓu thøc tÝnh An). NghÜa lµ
trôc x0 vu«ng gãc víi z0 vµ z1. Ta chän chiÒu
cña x0 tõ tr¸i sang ph¶i th× gãc quay α1=900
(chiÒu d−¬ng ng−îc chiÒu kim ®ång hå).
§ång thêi ta còng thÊy gèc O1 ®· tÞnh tiÕn
mét ®o¹n däc theo z0 , so víi O0, ®ã chÝnh lµ
phÐp biÕn ®æi Trans(0,0,d1) (tÞnh tiÕn däc theo
z0 mét ®o¹n d1) ; c¸c trôc y0,vµ y1 x¸c ®Þnh
theo qui t¾c bµn tay ph¶i (H×nh 3.12 ) .
TiÕp tôc chän gèc täa ®é O2 ®Æt trïng
víi O1 v× trôc khíp thø ba vµ trôc khíp thø
hai c¾t nhau t¹i O1 (nh− h×nh 3.12). Trôc z2
cïng ph−¬ng víi trôc khíp thø ba, tøc lµ ®·
quay ®i mét gãc 900 so víi z1 quanh trôc y1;
phÐp biÕn ®æi nÇy kh«ng cã trong biÓu thøc
tÝnh An nªn kh«ng dïng ®−îc, ta cÇn chän l¹i
vÞ trÝ ban ®Çu cña robot (thay ®æi vÞ trÝ cña
kh©u thø 3) nh− h×nh 3.13.
Theo h×nh 3.13, O2 vÉn ®−îc ®Æt trïng
víi O1, trôc z2 cã ph−¬ng th¼ng ®øng, nghÜa lµ
ta ®· quay trôc z1 thµnh z2 quanh trôc x1 mét
gãc -900 (tøc α2= -900).
§Çu cuèi cña kh©u thø 3 kh«ng cã
khíp, ta ®Æt O3 t¹i ®iÓm gi÷a cña c¸c ngãn
tay, vµ trôc z3, x3 chän nh− h×nh vÏ, nh− vËy
ta ®· tÞnh tiÕn gèc to¹ ®é däc theo z2 mét
®o¹n d3 (PhÐp biÕn ®æi Trans(0,0,d3)), v× ®©y
lµ kh©u tÞnh tiÕn nªn d3 lµ biÕn .
H
×nh 3.12 : G¾n c¸c h
Ö
to
¹
®
é
O
0
vµ O
1
y1
x1
y0
z1
z2
O1, O2
O0
z0
θ1
θ
2d3
x0
d
1
θ
1
θ
2d3
H
×nh 3.11 : Robot RR
T
≡ x2
O3
≡ O
2
≡ z2
z3
z0
O0x0
O1
y1
d
1
x1
y0
z1
θ1
θ
2
d3
x3
d3
×nh 3.13 : HÖ to¹ ®é
g¾n lªn c¸c kh©u
TS. Ph¹m §¨ng Ph−íc
Robot c«ng nghiÖp 34
Nh− vËy viÖc g¾n c¸c hÖ to¹ ®é lªn c¸c kh©u cña robot ®· hoµn thµnh. Th«ng qua c¸c
ph©n tÝch trªn ®©y, ta cã thÓ x¸c ®Þnh ®−îc c¸c th«ng sè DH cña robot.
2. LËp b¶ng th«ng sè DH :
Kh©u θiαiaidi
1 θ1
*90 0 d1
2 θi
*-90 0 0
3 0 0 0 d3
*
3. X¸c ®Þnh c¸c ma trËn A :
Ma trËn An cã d¹ng :
cosθ -sinθ cosαsinθ sinα 0
An = sinθ cosθ cosα-cosθ sinα0
0 sinα cosα d
0 0 0 1
Víi qui −íc viÕt t¾t : C1 = cosθ1 ; S1 = sinθ1 ; C2 = cosθ2 . . .
C
10 S10
A1 = S10 -C10
0 1 0 d1
0 0 0 1
C
20 -S20
A2 = S20 C20
0 -1 0 0
0 0 0 1
1 0 0 0
A3 = 0 1 0 0
0 0 1 d3
0 0 0 1
4. TÝnh c¸c ma trËn biÕn ®æi thuÇn nhÊt T :
+ Ma trËn 2T3 = A3
+ Ma trËn 1T3 = A2. 2T3
C
20 -S20 1 0 0 0 C20 -S2-S2*d3
1T3 = S20 C20 0 1 0 0 = S20 C2C2*d3
0 -1 0 d2 0 0 1 d3 0 -1 0 0
0 0 0 1 0 0 0 1 0 0 0 1
+ Ma trËn T3 = A1 . 1T3
C
10 S10 C20 -S2-S2*d3
T3 = S10 -C10 S20 C2C2*d3
0 1 0 d1 0 -1 0 0
0 0 0 1 0 0 0 1
TS. Ph¹m §¨ng Ph−íc
Robot c«ng nghiÖp 35
C
1C2-S1-C1S2-C1S2d3
= S1d2C1-S1S2-S1S2d3
S
20 C2C2d3 + d1
0 0 0 1
Ta cã hÖ ph−¬ng tr×nh ®éng häc cña robot nh− sau :
nx = C1C2;
Ox = -S1;
ax = -C1S2;
px = -C1S2d3
ny = S1C2;
Oy = C1;
ay = -S1S2;
py = -S1S2d3
nz = S2
Oz = 0;
az = C2;
pz = C2d3 + d1;
(Ta cã thÓ s¬ bé kiÓm tra kÕt qu¶ tÝnh to¸n b»ng c¸ch dùa vµo to¹ ®é vÞ trÝ px,py, pz ®·
tÝnh so víi c¸ch tÝnh h×nh häc trªn h×nh vÏ).
3.9. HÖ ph−¬ng tr×nh ®éng häc cña robot STANFORD :
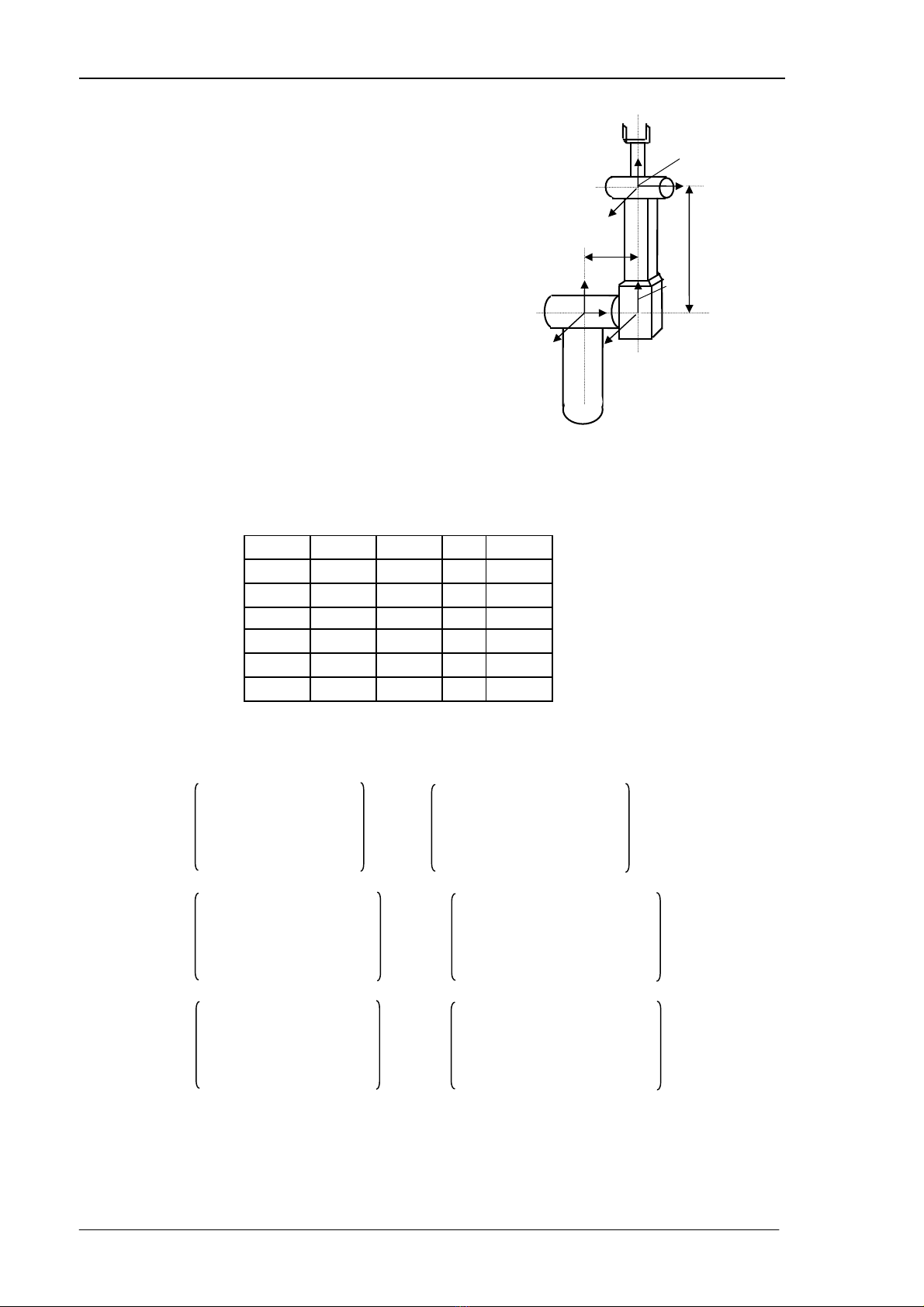
Stanford lµ mét robot cã 6 kh©u víi cÊu h×nh RRT.RRR (Kh©u thø 3 chuyÓn ®éng tÞnh
tiÕn, n¨m kh©u cßn l¹i chuyÓn ®éng quay). KÕt cÊu cña robot Stanford nh− h×nh 3.14 :
H×nh 3.14 : Robot Stanford
TS. Ph¹m §¨ng Ph−íc
Robot c«ng nghiÖp 36
Trªn h×nh 3.15 tr×nh bµy m« h×nh
cña robot Stanford víi viÖc g¾n c¸c hÖ to¹
®é lªn tõng kh©u. §Ó ®¬n gi¶n trong khi
viÕt c¸c ph−¬ng tr×nh ®éng häc cña robot,
ta qui −íc c¸ch viÕt t¾t c¸c hµm l−îng gi¸c
nh− sau :
C1 = cosθ1;
S1 = sinθ1;
C12 = cos(θ1+θ2);
S12 = sin(θ1+θ2)
S234 = sin (θ2+θ3+θ4) ... .
HÖ to¹ ®é g¾n lªn c¸c kh©u cña robot nh−
h×nh 3.15. (Kh©u cuèi cã chiÒu dµi vµ
kho¶ng c¸ch b»ng kh«ng, ®Ó cã thÓ g¾n c¸c
lo¹i c«ng cô kh¸c nhau nªn chän O6≡O5).
B¶ng th«ng sè DH (Denavit-Hartenberg) cña robot Stanford nh− sau :
Kh©u θiαiaidi
1 θ1* -9000 0
2 θ2* 9000 d2
3 0 0 0 d3*
4 θ4* -9000 0
5 θ5* 9000 0
6 θ6* 0 0 0
(* : C¸c biÕn khíp).
C¸c ma trËm A cña robot Stanford ®−îc x¸c ®Þnh nh− sau :
C
10 -S10 C20 S20
A1= S10 C10 A2=S
20 -C20
0 -1 0 0 0 1 0 d2
0 0 0 1 0 0 0 1
1 0 0 0 C40 -S40
A3= 0 1 0 0 A4=S
40 C40
0 0 1 d3 0 -1 0 0
0 0 0 1 0 0 0 1
C
50 S50 C6-S60 0
A5= S50 -C50 A6=S
6C60 0
0 1 0 0 0 0 1 0
0 0 0 1 0 0 0 1
d2d3
z4
z3,z5,z6
z2
O0,O1
x
i
x0
z0
z1
H
×nh 3.15 : HÖ to¹ ®é cña Robot Stanfor
d
O3,O4,O5,O6
x1
O2
TÝch cña c¸c ma trËn chuyÓn vÞ A ®èi víi robot Stanford ®−îc b¾t ®Çu ë kh©u 6 vµ
chuyÓn dÇn vÒ gèc; theo thø tù nÇy ta cã :
TS. Ph¹m §¨ng Ph−íc
Robot c«ng nghiÖp 37
C
6-S60 0
T65 = S6C60 0
0 0 1 0
0 0 0 1
C
5C6-C5S6S50
T64 = A5A6 =S
5C6-S5S6-C50
S
6C60 0
0 0 0 1
C
4C5C6 - S4S6-C4C5S6-S4C6C4S50
T63 = A4A5A6 =S
4C5C6 + C4S6-S4C5S6 + C4C6S4S50
-S5C6S5S6C50
0 0 0 1
C
4C5C6-S4S6-C4C5S6 - S4C6C4S50
T62 = A3A4A5A6 = S4C5C + C4S6-S4C5S6 + C4C6S4S50
-S5C6S5S6C5d3
0 0 0 1
C
2(C4C5C6 - S4S6) - S2S5C6-C2(C4C5S6-S4C6)+S2S5S6
T61 =A2 A3A4A5A6 = S2(C4C5C6 - S4S6) + C2S5C6-S2(C4C5S6+S4C6)-C2S5S6
S
4C5C6 + C4S6-S4C5S6+C4C6
0 0
C2C4S5 + S2C5S2d3
S2C4S5 - C2C5-C2d3
S4S5d2
0 1
Cuèi cïng :
n
xOxaxpx
T6 = nyOyaypy= A1T61
n
zOzazpz
0 0 0 1
§Ó tÝnh T6, ta ph¶i nh©n A1 víi T6
1 sau ®ã c©n b»ng c¸c phÇn tö cña ma trËn T6 ë hai vÕ
ta ®−îc mét hÖ thèng c¸c ph−¬ng tr×nh sau :
nx = C1[C2(C4C5C6 - S4S6) - S2S5C6] - S1(S4C5C6 + C4S6)
ny = S1[C2(C4C5C6 - S4S6) - S2S5C6] + C1(S4C5C6 + C4S6)
nz = -S2(C4C5C6 - S4S6) + C2S5C6
Ox = C1[-C2(C4C5S6 + S4C6) + S2S5S6] - S1(-S4C5S6 + C4C6)
Oy = S1[-C2(C4C5S6 + S4C6) + S2S5S6] + C1(-S4C5C6 + C4C6)
Oz = S2(C4C5S6 + S4C6) + C2S5S6
aX = C1(C2C4S5 + S2C5) - S1S4S5
ay = S1(C2C4S5 + S2C5) + C1S4S5
az = -S2C4S5 + C2C5
px = C1S2d3 - S1d2
py = S1S2d3 + C1d2
pz = C2d3
TS. Ph¹m §¨ng Ph−íc