- 50 -
Ch ng 5ươ
Đ C TR NG HÌNH H C C A M T C T NGANGẶ Ư Ọ Ủ Ặ Ắ
5.1. Khái ni m chung :ệ
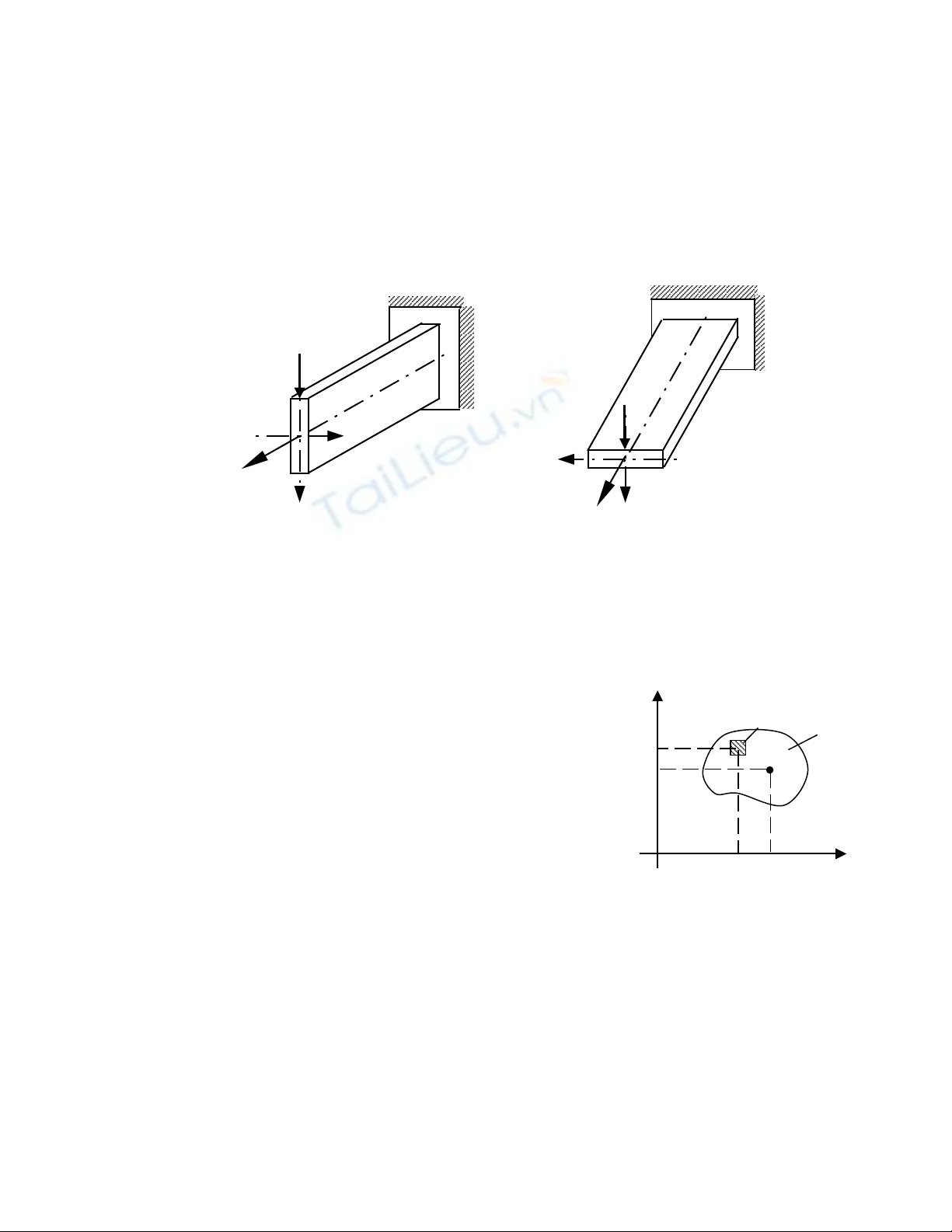
Xét 1 d m công xon ti t di n ch nh t có c nh (b ầ ế ệ ữ ậ ạ × h) v i h > b cùng chi uớ ề
dài, cùng m t lo i v t li u, cùng ch u m t l c P nh nhau trong 2 tr ng h p :ộ ạ ậ ệ ị ộ ự ư ườ ợ
ti t di n đ đ ng (Hình 5.1a) và ti t di n n m ngang (Hình 5.1b).ế ệ ể ứ ế ệ ằ
B ng tr c giác ta nh n ra là tr ng h p (a) ch u l c t t h n tr ng h p thằ ự ậ ườ ợ ị ự ố ơ ườ ợ ứ
(b). M t khác ta th y ng su t tr ng h p (b) g p 4 l n tr ng h p (a) vàặ ấ ứ ấ ở ườ ợ ấ ầ ở ườ ợ
đ võng l i g p 16 l n.ộ ạ ấ ầ
Nh v y rõ ràng s c ch u c a m t thanh không nh ng ch tuỳ thu c vào lo iư ậ ứ ị ủ ộ ữ ỉ ộ ạ
v t li u mà còn tuỳ thu c vào hình d ng c a m t c t ngang và s phân b c aậ ệ ộ ạ ủ ặ ắ ự ố ủ
v t li u trên m t c t. Nh ng y u t đó đ c th hi n trong nh ng đ c tr ngậ ệ ặ ắ ữ ế ố ượ ể ệ ữ ặ ư
hình h c c a m t c t đ c nghiên c u sau đây:.ọ ủ ặ ắ ượ ứ
5.2. Momen tĩnh:
5.2.1. Momen tĩnh đ i v i 1 tr c:ố ớ ụ
Đ nh nghĩa : ị
∫∫ ==
F
y
F
xxdFS;ydFS
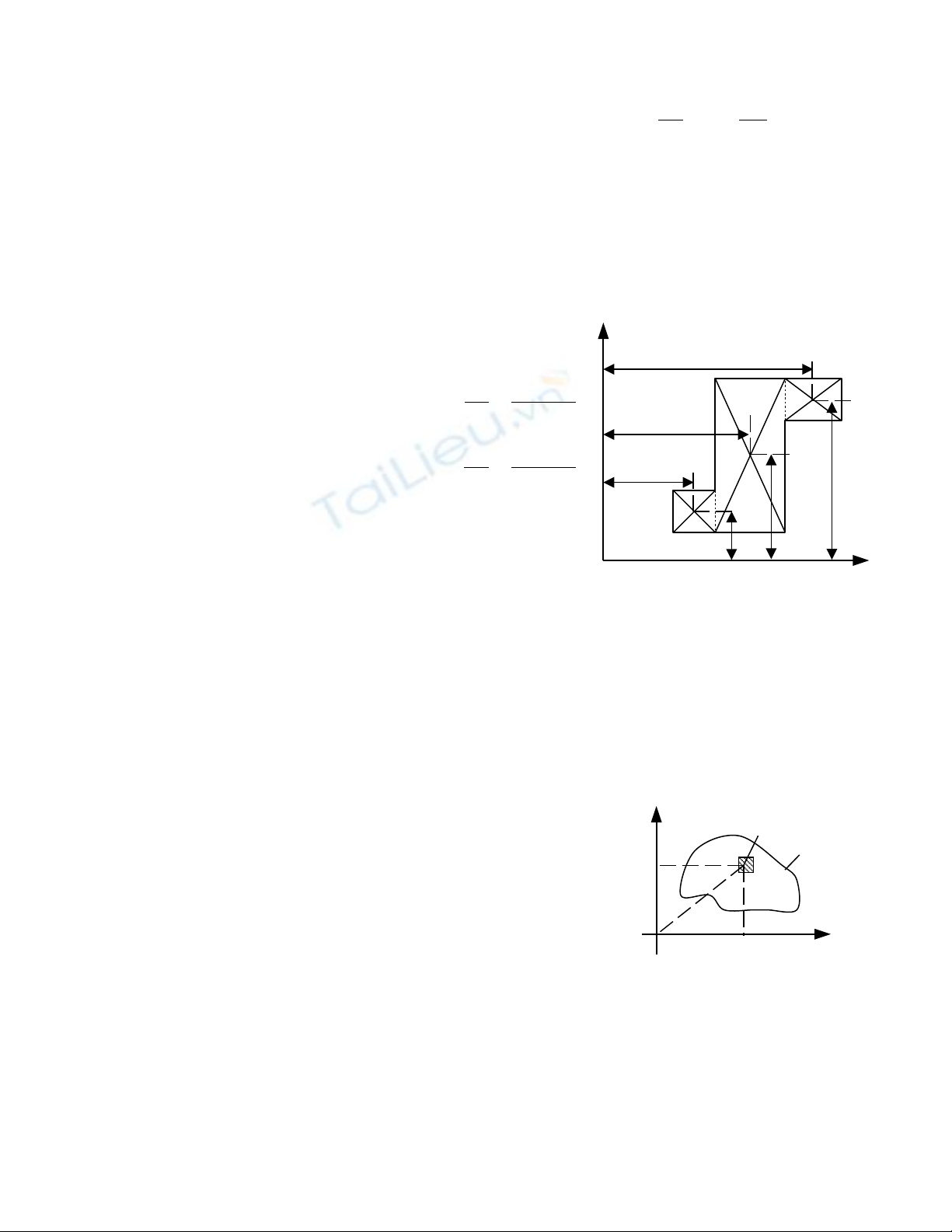
Sx , Sy là moment tĩnh c a di n tích m t c tủ ệ ặ ắ
ngang đ i v i tr c x, y.ố ớ ụ
Th nguyên c a Sứ ủ x , Sy là (chi u dài)ề3.
Vì x, y có th âm ho c d ng nên momenể ặ ươ
tĩnh có th có tr s âm ho c d ng.ể ị ố ặ ươ
5.2.2. H qu :ệ ả
a) Khi momen tĩnh c a di n tích F đ i v i tr c nào b ng 0 thì tr c đó g i làủ ệ ố ớ ụ ằ ụ ọ
tr c trung tâmụ.
b) Giao đi m c a 2 tr c trung tâm g i là ể ủ ụ ọ tr ng tâmọ c a m t c t .ủ ặ ắ
G i xọc , yc là to đ tr ng tâm c a 1 hình, ta có : Sạ ộ ọ ủ x = F.yc , Sy = F.xc
( v i F là di n tích m t c t ngang )ớ ệ ặ ắ
Hình 5.1
P
x
y
z
z
P
x
y
Hình 5.2
x
dF F
y
y
yC
xC
x
C
O
(b)
(a)
- 51 -
T đó suy ra to đ tr ng tâm c a m t c t : ừ ạ ộ ọ ủ ặ ắ
F
S
y,
F
S
xX
c
y
c==
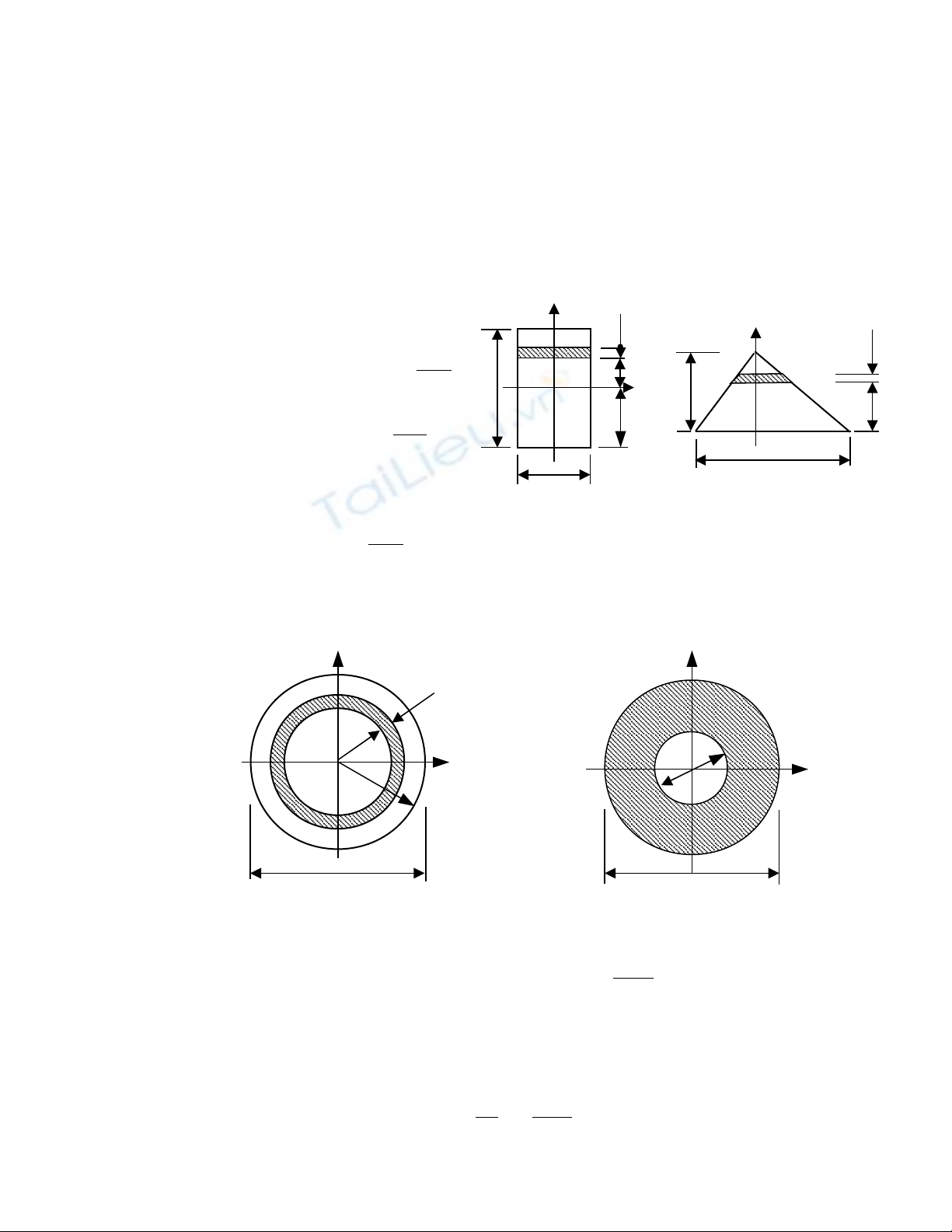
c) Đ tính momen tĩnh c a các hình ph ct p ta ph i chia nó thành nhi u hình ể ủ ứ ạ ả ề
đ n gi n mà di n tích ( Fơ ả ệ i ) và to đ tr ng tâm c a chúng ( xạ ộ ọ ủ i , yi) đã bi t tr c.ế ướ
Khi đó ta có :
∑
=
=+++= n
iiinnx y.Fy.F...y.Fy.FS
1
2211
∑
=
=+++= n
iiinny x.Fx.F...x.Fx.FS
1
2211
To đ tr ng tâm m t c t : ạ ộ ọ ặ ắ
∑
∑
∑
∑
==
==
i
ii
x
c
i
ii
y
c
F
y.F
F
S
y
F
x.F
F
S
x
5.3. Momen quán tính c a m t c t ngang:ủ ặ ắ
5.3.1. Momen quán tính đ i v i 1 tr c :ố ớ ụ
∫≥=
F
xdFyJ 0
2
∫≥=
F
ydFxJ 0
2
Th nguyên c a momen quán tính: (chi u dài )ứ ủ ề 4. Đ n v : mơ ị 4, cm4, ….
5.3.2. Momen quán tính đ c c c ộ ự :
∫≥ρ=
F
2
p0dFJ
Vì
222 yx +=ρ
nên Jp = Jx + Jy
5.3.3. Momen quán tính ly tâm v i h tr c (x,y)ớ ệ ụ
∫
=
F
xy dF.xyJ
vì
0,J0,y,x
xy
≥≤→≥≤
5.3.4. Tính ch tấ :
a) Khi momen quán tính ly tâm đ i v i h tr c nào đó b ng 0 thì h tr c đó ố ớ ệ ụ ằ ệ ụ
Hình 5.3
y
x
x1
x2
x3
y1
y2
y3
O
Hình 5.4
O
x
y
y
ρ
x
dF
F
- 52 -
đ c g i là đ c g i là ượ ọ ượ ọ h tr c quán tính chínhệ ụ . N u h tr c quán tính chính quaế ệ ụ
tr ng tâm m t c t thì đ c g i là ọ ặ ắ ượ ọ h tr c quán tính chính trung tâm.ệ ụ
b) T i b t kỳ đi m nào trên m t ph ng c a m t c t ta cũng có th xác đ nh ạ ấ ể ặ ẳ ủ ặ ắ ể ị
đ c m t h tr c quán tính chính.ượ ộ ệ ụ
c) N u m t c t có 1 tr c đ i x ng thì b t kỳ tr c nào vuông góc v i tr c đ iế ặ ắ ụ ố ứ ấ ụ ớ ụ ố
x ng đó cũng l p v i nó thành m t h tr c quán tính chính.ứ ậ ớ ộ ệ ụ
5.3.5. Momen quán tính c a 1 s hình đ n gi n ủ ố ơ ả :
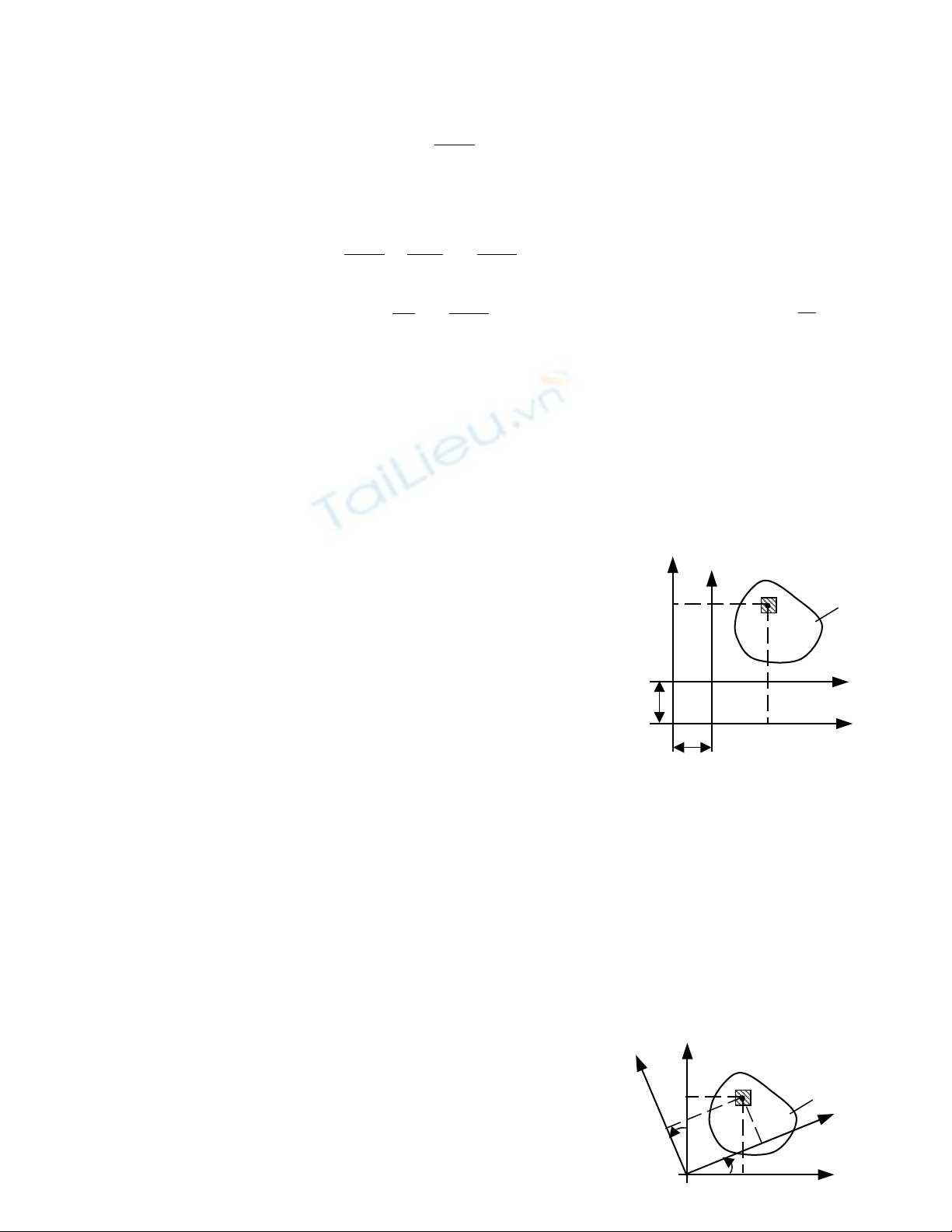
a) Hình ch nh t: (Hình 5.5a)ữ ậ
∫ ∫
+
−
===
F
/h
/h
x
bh
bdyydFyJ
2
2
3
22
12
T ng t : ươ ự
12
hb
J
3
y=
b) Hình tam giác : (Hình 5.5b)
12
3
bh
Jx=
c) Hình tròn – hình vành khăn :
- Hình tròn: (Hình 5.6a)
Vì
ρπρ= ddF 2
, momen quán tính đ c c c là :ộ ự
∫ ∫ π
=ρρπ=ρ=
F
R
0
4
32
p2
R
d2dFJ
Do tính ch t đ i x ng nên ta nh n th y ngay Jấ ố ứ ậ ấ x = Jy , do đó ta có :
Jp = Jx + Jy = 2 Jx = 2Jy.
Suy ra :
4
R
2
J
JJ
4
p
yx
π
===
Hình 5.5
x
y
b
dy
h/2
y
h
a) b)
b
y
dy
y
h
Hình 5.6 b)
D
d
y
x
dρ
ρ
y
x
R
Da)
- 53 -
N u g i D là đ ng kính đ ng tròn thì các công th c trên có th vi t l i :ế ọ ườ ườ ứ ể ế ạ
4
yx
4
4
pD05,0JJ;D1,0
32
D
J==≈
π
=
- Hình vành khăn: (Hình 5.6b).
( ) ( )
444
444
p1D1,01
32
D
32
d
32
D
Jη−≈η−
π
=
π
−
π
=
( ) ( )
444
4
p
yx 1D05,01
64
D
2
J
JJ η−≈η−
π
===
, v i ớ
D
d
=η
.
5.4. Momen quán tính đ i v i h tr c song song :ố ớ ệ ụ
Bi t Jếx , Jy ,Jxy đ i v i hốớệ tr c Oxy. Tìm JụX , JY ,JXY đ i v i h tr c song songố ớ ệ ụ
O1XY.
Công th c chuy n tr c : ứ ể ụ
+=
+=
byY
axX
Do đó :
( )
∫∫ +==
F
2
F
2
XdFbydFYJ
( )
∫∫ +==
F
2
F
2
YdFaxdFXJ
( )( )
∫∫
++==
FF
XY dFbyaxXYdFJ
Khai tri n và rút g n ta đ c : ể ọ ượ
x
2
xX
bS2FbJJ ++=
y
2
yY aS2FaJJ ++=
yxxyXY bSaSabFJJ +++=
Tr ng h p đ c bi t : N u Oxy là h tr c trung tâm, ta có Sườ ợ ặ ệ ế ệ ụ x = Sy = 0, khi
đó công th c trên ch thành: ứ ở
FbJJ xX 2
+=
FaJJ yY 2
+=
abFJJ xyXY +=
Ta nh n th y momen quán tính đ i v i tr c trung tâm là nh nh t so v i tr cậ ấ ố ớ ụ ỏ ấ ớ ụ
nào // v i nó .ớ
5.5. Công th c xoay tr c v i momen quán tính – H tr c quán tính chính:ứ ụ ớ ệ ụ
Hình 5.7
x x
y
y
b
dF F
O
O1
Y
X
a
M
Y
X
Hình 5.8
u
x
y
ydF F
O
v
M
x
v u

- 54 -
Bi t Jếx , Jy ,Jxy đ i v i hốớệ tr c Oxy.ụ
Tìm JX , JY ,JXY đ i v i h tr c Ouv h pố ớ ệ ụ ợ
v i tr c x m t góc ớ ụ ộ α theo chi u d ngề ươ
l ng giác .ượ
Công th c xoay tr c : ứ ụ
α−α=
α+α=
sinxcosyv
sinycosxu
(i)
Theo đ nh nghĩa ta có : ị
∫
=
F
udFvJ 2
;
∫
=
F
vdFuJ 2
;
dFuvJ
F
uv ∫
=
(j)
Thay công th c xoay tr c vào (j) , khai tri n và rút g n ta đ c :ứ ụ ể ọ ượ
( )
α+α−=
αα+α+α=
αα−α+α=
2cosJ2sinJJ
2
1
J
sincosJ2cosJsinJJ
sincosJ2sinJcosJJ
xyyxuv
xy
2
y
2
xv
xy
2
y
2
xu
Bi n đ i ta suy ra :ế ổ
( ) ( )
( ) ( )
( )
α+α
−
=
α+α
−
−
+
=
α−α
−
+
+
=
2cosJ2sin
2
JJ
J
2sinJ2cos
2
JJ
2
JJ
J
2sinJ2cos
2
JJ
2
JJ
J
xy
yx
uv
xy
yxyx
v
xy
yxyx
u
5.5.1. H quệ ả :
a)
yxvu JJJJ +=+
b) H tr c quán tính chính ệ ụ
0=⇒ uv
J
yx
xy
JJ
J
tag −
−=α⇔ 2
2
c)
( )
2
xy
2
yx
yx
max
J4JJ
2
1
2
JJ
J+−+
+
=
d)
( )
2
xy
2
yx
yx
min J4JJ
2
1
2
JJ
J+−−
+
=
Ngoài ra ta có th bi u di n MMQT c a m t hình v i 1 tr c nh sau:ể ể ễ ủ ộ ớ ụ ư
F/JiF.iJ xx
2
xx =⇒=
F/JiF.iJ yy
2
yy =⇒=
(ix , iy g i là bán kính quán tính [mọ2]. )


![Chương trình khung trình độ cao đẳng nghề Cắt gọt kim loại - Trường CĐN KTCN Dung Quất [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2021/20210417/tradaviahe20/135x160/1301618651048.jpg)
![Tổng hợp 58 câu hỏi về đồ án Chi tiết máy [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2020/20201015/daohachi0512/135x160/9011602770055.jpg)






















