SỞ GIÁO DỤC VÀ ðÀO TẠO
TỈNH HẢI DƯƠNG
TRƯỜNG THPT ðOÀN THƯỢNG
KÌ THI THỬ ðẠI HỌC LẦN 2 NĂM 2010
MÔN TOÁN, KHỐI A
ðÁP ÁN VÀ BIỂU ðIỂM CHẤM
* Chú ý. Thí sinh làm bài không theo cách nêu trong ñáp án mà vẫn ñúng thì cho ñủ
ñiểm từng phần tương ứng.
Câu ý
Nội dung ðiểm
I 1
Khảo sát hàm số
= − + +
4 2
3 4
y x x (C) 1,00
TXð:
.
lim
x
y
→±∞
= −∞
,
3
0 4
' 4 6 , ' 0
6 25
2 4
x y
y x x y
x y
= − + = ⇔ = ± ⇒ =
BBT: ghi ñầy ñủ
Kết luận về tính ñb, nb, cực trị
2
2 21
'' 12 6, '' 0
2 4
y x y x y
= − + = ⇔ = ± ⇒ =
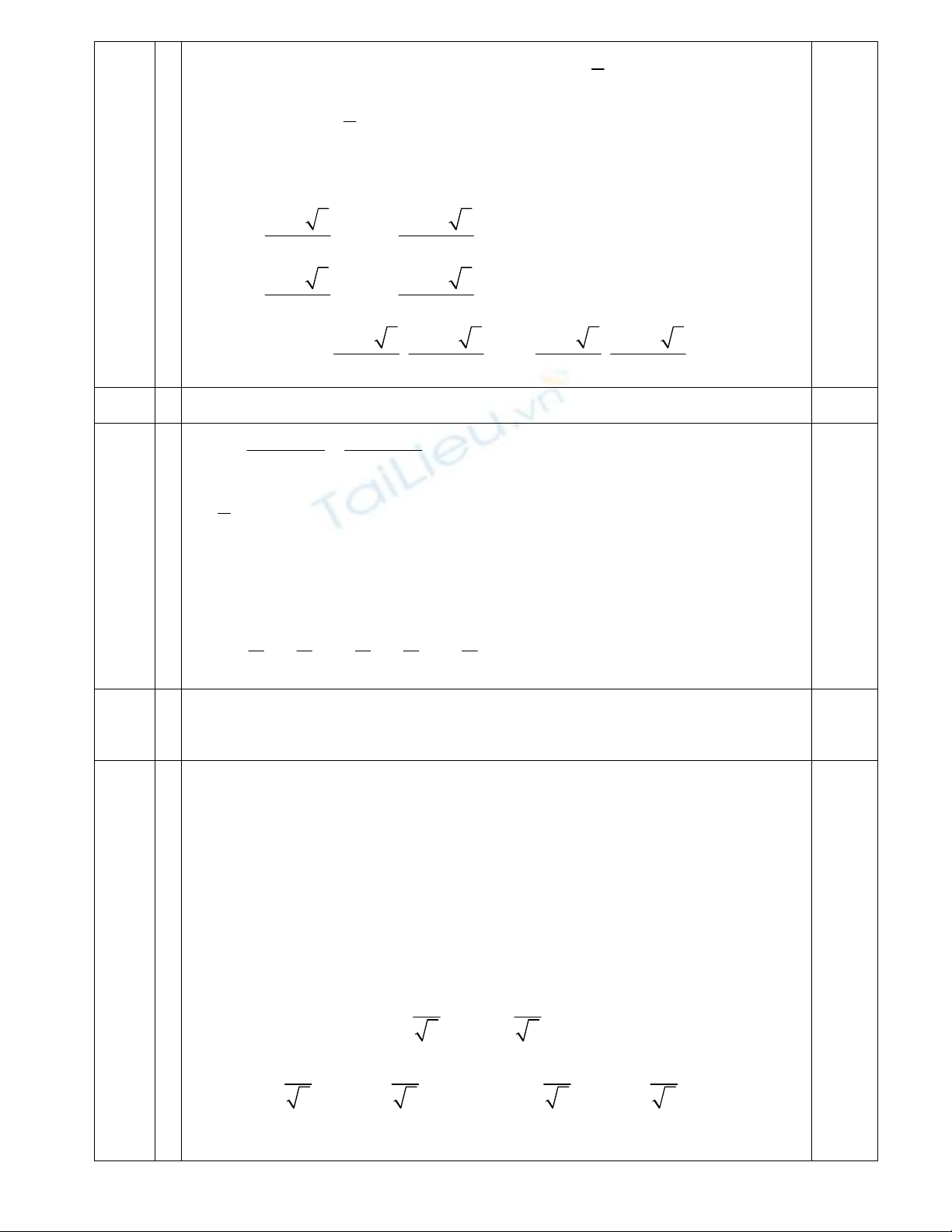
ðồ thị. ðồ thị là ñường cong trơn thể hiện ñúng tính lồi, lõm.
ðồ thị ñi qua 7 ñiểm:
6 25 2 21
( 2;0), ; , ; ,(0;4)
2 4 2 4
± ± ±
6
5
4
3
2
1
-1
-2
-6 -4 -2 2 4 6
Nhận xét. ðồ thị hàm số nhận trục tung làm trục ñối xứng
0,25
0,25
0,25
0,25
I 2
Tìm M thuộc (C) sao cho tiếp tuyến tại M vuông góc với
2 4 0
x y
+ − =
1,00
(
)
4 2
0 0 0
( ) ; 3 4
M C M x x x
∈ ⇒ − + +
. Tiếp tuyến của (C) tại M có hệ số góc
3
0 0 0
'( ) 4 6
f x x x
= − +
ðường thẳng
2 4 0
x y
+ − =
có hệ số góc bằng
1
2
−
Ycbt
3
0 0 0
1
'( ). 1 4 6 2 0
2
f x x x
⇔ − = − ⇔ − + =
0 0
0 0
0 0
1 6
1 3 21 2 3
2 4
1 3 21 2 3
2 4
x y
x y
x y
= ⇒ =
− + −
⇔ = ⇒ =
− − +
= ⇒ =
Vậy
( )
1 3 21 2 3 1 3 21 2 3
1;6 , ; , ;
2 4 2 4
M M M
− + − − − +
0,25
0,25
0,25
0,25
II 1
Giải phương trình
2 2 2
sin sin 2 sin 3 2
x x x
+ + =
(1)
1,00
(1)
2
1 cos2 1 cos6
sin 2 2
2 2
x x x
− −
⇔ + + =
2 2
1
(cos2 cos6 ) 1 sin 2 0 cos2 cos4 cos 2 0
2
x x x x x x
⇔ + + − = ⇔ + =
cos2 0 cos2 0
cos2 cos4 0 cos2 cos( 4 )
x x
x x x x
π
= =
⇔ ⇔
+ = = −
, ,
4 2 6 3 2
x k x k x k
π π π π π
π
⇔ = + = + = −
0,25
0,25
0,25
0,25
2
Giải hệ phương trình:
2 2
2
2( ) 7
2 2 10
x y x y
y xy x
+ + + =
− − =
.
1,00
Hệ
2 2
2 2
( 1) ( 1) 9
( ) ( 1) 9
x y
y x x
+ + + =
⇔
− − + =
ðặt
1, 1
a x b y b a y x
= + = + ⇒ − = −
ta ñược hệ
2 2
2 2
9
( ) 9
a b
b a a
+ =
2 2 2 2 2
( ) 2 0
a b b a a a ab a
⇒ + = − − ⇔ = − ⇔ =
hoặc
2
a b
= −
0 3 1, 2
a b x y
= ⇒ = ± ⇒ = − =
hoặc
1, 4
x y
= − = −
2
3 6
2 5 9
5 5
a b b b a
= − ⇒ = ⇔ = ± ⇒ =
m
6 3
1 , 1
5 5
x y
⇒ = − − = − +
hoặc
6 3
1 , 1
5 5
x y
= − + = − −
Kết luận. Hệ có 4 nghiệm như trên
0,25
0,25
0,25
0,25
* Chú ý. Học sinh có thể rút
2
10
2( 1)
y
xy
−
=
+
từ pt thứ hai và thế vào pt thứ
nhất ñược
4 3 2
5 20 24 88 32 0
y y y y
+ − − + =
2
( 2)( 4)(5 10 4) 0
y y y y
⇔ − + + − =
3 3
2, 4, 1 , 1
5 5
y y y y⇔ = = − = − + = − −
6 6
1, 1, 1 , 1
5 5
x x x x⇒ = − = − = − − = − +
0,5
0,25
0,25
III Tìm giới hạn I =
0
5 1 2 cos
lim
x
x
x x
x
→
+ −
1,00
ðặt
( ) 5 1 2 cos (0) 0
x
f x x x f
= + − ⇒ =
I =
0
( ) (0)
lim '(0)
0
x
f x f f
x
→
−
=
−
1
'( ) 5 ln5 1 2 5 . sin
1 2
x x
f x x x
x
= + + +
+
I '(0) ln5 1
f
⇒ = = +
Cách khác
.
(
)
(
)
( )
0 0
5 1 2 1 5 1 1 cos
5 1 2 cos
lim lim
x x
x
x x
x x
x x
x x
→ →
+ − + − + −
+ − =
(
)
( )
( )
0
5 1 2 1 5 1 1 cos
lim
xx
x
x
x
x x x
→
+ − −−
= + +
Tính ñược
(
)
0 0
5 1 2 1 5 .2
lim lim 1
1 2 1
xx
x x
x
xx
→ →
+ −
= =
+ +
Tính ñược
ln5
0 0
5 1 1
lim lim .ln5 ln5
ln5
x x
x x
e
x x
→ →
− −
= =
Tính ñược
2
2
0 0
2sin
1 cos 2
lim lim . 0
4
2
x x
x
x x
xx
→ →
−
= =
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
IV Tính thể tích khối tứ diện SMNC
1,00
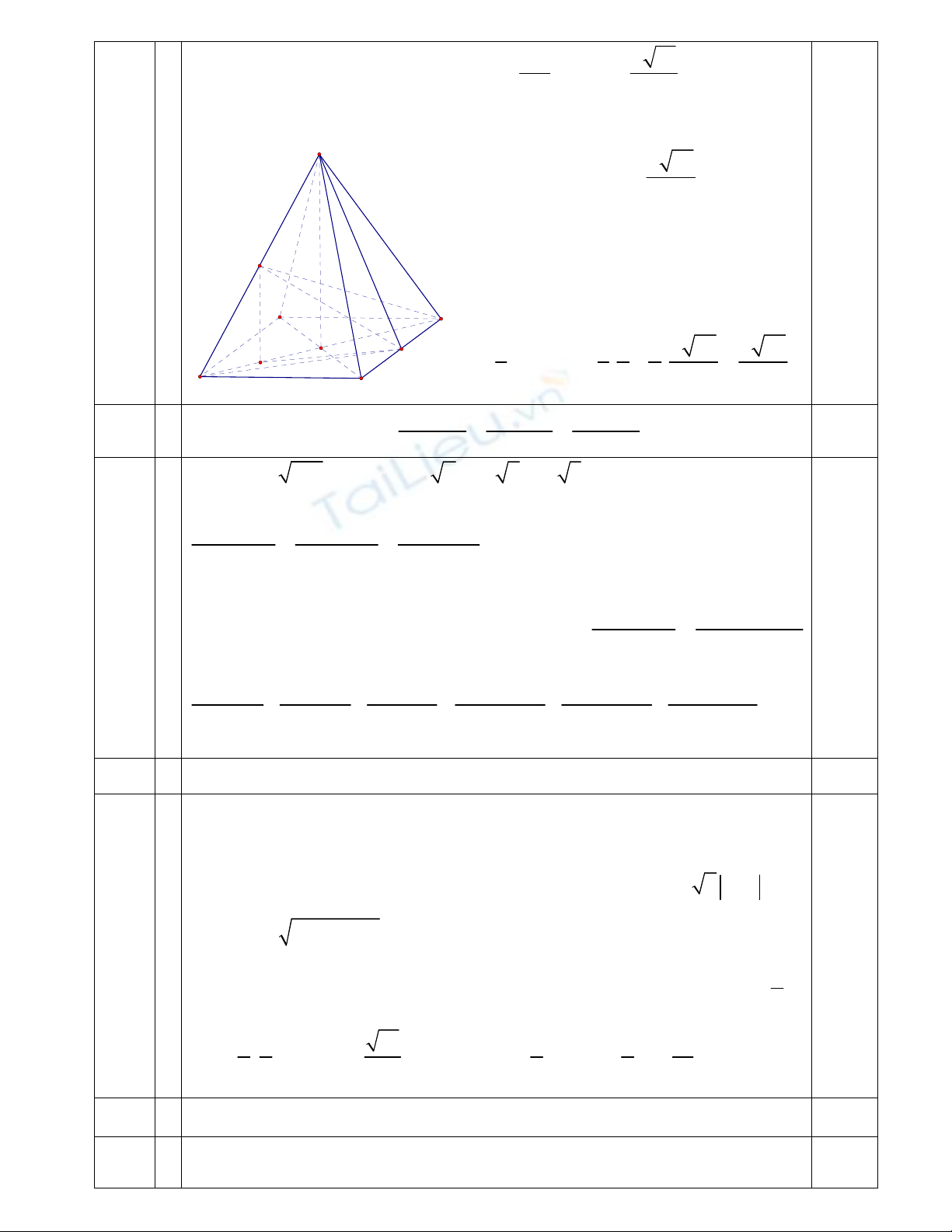
Gọi O là tâm của hình vuông ABCD suy ra SO
⊥
(ABCD). Gọi H là trung
ñiểm của AO thì MH // SO nên MH
⊥
(ABCD) suy ra HN là hình chiếu
của MN trên mp(ABCD). Bởi vậy góc giữa MN và (ABCD) là góc
0
60
MNH MNH
∠ ⇒ ∠ =
.
0,25
2
2 2 2 0
5 10
2 . .cos45
8 4
a a
HN CH CN CH CN HN= + − = ⇒ =
Tam giác MNH vuông suy ra
0
30
.tan30
4
a
MH HN= =
SA cắt (MNC) tại ñiểm M là trung
ñiểm của SA nên
( ;( )) ( ;( ))
S MNC A MNC
d d
=
SMNC AMNC
V V
⇒ =
1 1 1 30 30
. . .
3 3 2 2 4 48
ANC
a a a
S MH a= = =
0,25
0,25
0,25
V Chứng minh rằng 1 1 1
1
1 1 1
a b b c c a
+ + ≤
+ + + + + +
1,00
3
1 1
abc abc
= ⇔ =
. ðặt
3 3 3
, ,
x a y b z c
= = = . Bài toán trở thành
Cho
, ,
x y z
dương thỏa mãn
1
xyz
=
. Chứng minh rằng
3 3 3 3 3 3
1 1 1
1
1 1 1
x y y z z x
+ + ≤
+ + + + + +
Bằng biến ñổi tương ñương chứng minh ñược
3 3
( )
x y xy x y
+ ≥ +
3 3
3 3
1 1
1 ( ) ( )
1 ( )
x y xy x y xyz xy x y z
x y xy x y z
⇒ + + ≥ + + = + + ⇒ ≤
+ + + +
Tương tự, cộng lại ta ñược
3 3 3 3 3 3
1 1 1 1 1 1
1
1 1 1 ( ) ( ) ( )
x y y z z x xy x y z yz x y z zx x y z
+ + ≤ + + =
+ + + + + + + + + + + +
ðẳng thức xảy ra
1
x y z
⇔ = = =
hay
1
a b c
= = =
0,25
0,25
0,25
0,25
VI.a 1
Viết phương trình ñường tròn
1,00
ðường trung trực của AB có pt y = x. (C) ñi qua A và B suy ra tâm I của
(C) thuộc ñường thẳng y = x
( ; )
I t t
⇒
.
Gọi H là hình chiếu của I trên MN
1, ( ; ) 2 2
MH IH d I t
⇒ = = ∆ = −
,
2 2
(1 )
IM IA t t
= = − +
.
IMH
∆
vuông
2 2 2 2 2 2
4
(1 ) 2( 2) 1
3
MI IH MH t t t t
⇒ = + ⇔ − + = − + ⇔ =
4 4 17
; ,
3 3 3
I R IA
⇒ = =
. Pt (C) là
2 2
4 4 17
3 3 9
x y
− + − =
0,25
0,25
0,25
0,25
2
Tìm ñiểm D thuộc ∆ sao cho thể tích khối tứ diện DABC bằng 8 1,00
(3; 1; 1), (2;2;2) , (0; 8;8)
AB AC AB AC
= − − = ⇒ = −
uuur uuur uuur uuur
HN
M
O
B
D
C
A
S
1
, 4 2
2
ABC
S AB AC
= =
uuur uuur
. Mp(ABC) có phương trình
1 0
y z
− + − =
( ;( ))
3 6
(1 2 ;2 ; 3 4 ).
2
M ABC
t
D D t t t d
−
∈∆ ⇒ − + − + =
( ;( ))
3 6
1 1
. .4 2. 4 2
3 3
2
DABC ABC M ABC
t
V S d t
−
= = = −
4
8 4 2 8
0
DABC
t
V t
t
=
= ⇔ − = ⇔
=
Vậy
( 7;6;13)
D
−
và
(1;2; 3)
D
−
0,25
0,25
0,25
0,25
VII.a
chọn 3 học sinh giỏi có cả Nam và Nữ và có ñủ cả ba khối 1,00
Chọn HS khối 10 có 5 cách
TH 1. Chọn HS khối 11 là Nam có 4 cách, khi ñó HS khối 12 phải chọn là
Nữ nên có 3 cách. Trường hợp này có 5.4.3 = 60 cách.
TH 2. Chọn HS khối 11 là Nữ có 2 cách, khi ñó HS khối 12 ñược chọn tùy
ý nên có 7 cách. Trường hợp này có 5.2.7 = 70 cách
Vậy có tất cả 60 + 70 = 130 cách
0,25
0,25
0,25
0,25
VI.b 1
Trong mặt phẳng Oxy, cho ñiểm
( 1;3)
M
−
. Viết phương trình ñường thẳng
∆ ñi qua M và tạo với hai trục tọa ñộ một tam giác có diện tích bằng 2.
1,00
Giả sử ∆ cắt Ox tại A(a ; 0), cắt Oy tại B(0 ; b) với
0
ab
≠
. Khi ñó pt ∆ là
1
x y
a b
+ =
. ∆ qua M nên 1 3 1 3
b a ab
a b
−
+ = ⇔ − + =
∆ tạo với hai trục tam giác OAB có diện tích bằng 2
1
2 4
2
ab ab
⇔ = ⇔ = ±
TH 1.
2
2, 2
3 4
3 4
42
4
3 4 4 0 , 6
3
a b
b a
b a
ab ab a a a b
= =
= −
− + =
= ⇒ ⇔ ⇔
−
=
− − = = = −
TH 2.
2
3 4
3 4
44
3 4 4 0
b a
b a
ab ab a a
= +
− + = −
= − ⇒ ⇔
= −
+ + =
(vô nghiệm)
Vậy có 2 ñường thẳng là
2 0
x y
+ − =
và
9 6 0
x y
+ + =
0,25
0,25
0,25
0,25
2
Tìm m ñể ∆ cắt (S) tại hai ñiểm M, N sao cho MN = 8 1,00
Mặt cầu (S)
+ + − + = −
2 2 2
(x 2) (y 3) z 13 m
có tâm
( 2;3;0)
I
−
và bán kính