Đề cương bài giảng Đại số và Hình học giải tích: Chuẩn nhất

ĐỀ CƯƠNG BÀI GIẢNG

Học phần: ĐẠI SỐ & HÌNH HỌC GIẢI TÍCH Đơn vị: Bộ môn Toán, Khoa CNTT

Thời gian: Tuần 1 Tiết 1-4

GV giảng 4, HV tự học: 4

Giáo viên: Nguyễn Trọng Toàn

Chươn

1 TẬP HỢP VÀ ÁNH XẠ

Các mục

1.1 Mệnh đề toán học và các phép toán logic

1.2 Tập hợp

1.3 Ánh xạ

Mục đích -

yêu cầu

- Giới thiệu mục đích, ý nghĩa của môn học

- Nắm được nội dung cơ bản của lý thuyết tập và khái niệm ánh xạ.

NỘI DUNG

I. LÝ THUYẾT

Chương I. TẬP HỢP VÀ ÁNH XẠ

1.1 MỆNH ĐỀ TOÁN HỌC VÀ CÁC PHÉP TÍNH LOGIC

1.1.1 Mệnh đề toán học: Là những khẳng định mang một ý nghĩa đúng hoặc sai. Không có mệnh đề

nửa đúng nửa sai.

Thí dụ 1.1 “ 5 > 3” : Mệnh đề đúng

“Áo bộ đội màu nâu” : Mệnh đề sai.

1.1.2 Các phép toán logic trên các mệnh đề. Giả sử ta có các mệnh đề A, B, C…

a) Phép phủ định

: Mệnh đề

nhận giá trị đúng khi A sai, nhận giá trị sai khi A đúng.

b) Phép Hội : Mệnh đề

B chỉ nhận giá trị đúng khi và chỉ khi A và B cùng đúng.

c) Phép Tuyển : Mệnh đề

B chỉ nhận giá trị sai khi và chỉ khi A và B cùng sai.

d) Phép kéo theo : Mệnh đề A  B chỉ nhận giá trị sai khi và chỉ khi A đúng và B sai.

e) Phép Tuyển loại trừ : Mệnh đề A  B nhận giá trị đúng khi A đúng và B sai hoặc A sai B

đúng.

Bảng chân trị

A B



B

B



B

1.1.3 Điều kiện cần, điều kiện đủ

Nếu

B thì A được gọi là điều kiện đủ của B, B được gọi là điều kiện cần có của A.

Nếu

Bthì A được gọi là điều kiện cần và đủ của B và ngược lại.

1.1.4 Vị từ

Như đã biết, mệnh đề là một câu khẳng định có ý nghĩa đúng hoặc sai rõ ràng. Tuy nhiên, trong

thực tế có những câu khẳng định mà giá trị chân lý của nó đúng hay sai tùy thuộc vào một hay nhiều

yếu tố chưa cụ thể (biến) nào đó.

Thí dụ 1.2 Khằng định “ x>5” có giá trị là đúng nếu x=7 và có giá trị là sai nếu x=2.

a) Hàm mệnh đề. Hàm





,,,

xx xxác định trên tập A được gọi là hàm mệnh đề n-ngôi trên

nếu A thay 112 2

, , ,

ax a x a với i



, 1,in thì





,,,

aa alà một mệnh đề.

Thí dụ 1.3 P(x) = “x>5” : Là hàm mệnh đề 1 ngôi trên R;

P(x,y,z) = “x>y, y>z” : Là hàm mệnh đề 3 ngôi trên R .

Trong các vị từ người ta thường sự dụng các lượng từ: Lượng từ riêng , đọc là “ tồn tại”,

“có” hay “ có ít nhất một”…hay Lượng từ chung



, đọc là “ với mọi”, “ tất cả”,…

Sự kết hợp giữa một hay nhiều lượng từ và một hàm mệnh đề tạo ra mệnh đề. Những mệnh đề

như vậy gọi là vị từ.

Thí dụ 1.4  x P(x): Là khẳng định tồn tại ít nhất x để P(x) đúng;

 x P(x) : Là khẳng định với mọi giá trị x P(x) đều đúng.

 x y P(x,y): Là khẳng định tồn tại ít nhất 1 giá trị x để P(x,y) đúng với mọi giá trị y.

b) Phép toán phủ định của vị từ

i) P(x) = x ( )

PX

ii) P(x) = x ( )

PX

Thí dụ 1.5 Để định nghĩa dãy {an} có giới hạn là a, người ta viết:

0, ,

kN nk a a



     

Vì vậy, để khẳng định {an} phân kỳ hoặc không phải có giới hạn là a, ta cần chỉ ra:

0 , , sao cho

kNnk a a



    

Hệ quả :

i) P(x) Q(x) P(x) Q( )

xx

ii) P(x) Q(x) P(x) Q( )

xx

1.2 TẬP HỢP

1.2.1 Khái niệm tập hợp

Tập hợp là một khái niệm cơ bản, không định nghĩa. Tuy nhiên có thể giải thích: Một tập hợp

bao gồm các đối tượng xác định hợp thành. Mỗi đối tượng gọi là một phần tử của tập hợp.

Kí hiệu các tập hợp: A, B, C... Nếu x là một phấn tử của tập A ta viết xA, còn nếu y không phải

là phần tử của tập A ta viết xA.

1.2.2 Mô tả một tập hợp: Có 2 phương pháp

a) Liệt kê các phần tử của tập hợp.

Thí dụ 1.6 S ={1,2,3,a,c}. Khi đó : 3,aS và 5,6,bS.

b) Nêu các tính chất đặc trưng của phần tử.

Thí dụ 1.7 B = {số nguyên, dương chẵn}. Khi đó 2,4,8B và 1,13,-8B

c) Một số tập hợp đặc biệt

- Tập rỗng  ={}

- Tập số tự nhiên N ={0,1,2,3,...}

- Tập số nguyên Z = {0,  1, 2, 3...}

- Tập số hữu tỷ Q = {p/q p,qZ , q0}

- Tập số thực R = { Các số hữu tỷ và vô tỷ}

d) Hai tập A và B được gọi là hai tập bằng nhau: Nếu chúng có cùng các phần tử

A = B  (xA xB) (yB  yA)

e) Bao hàm và tập con.

Tập hợp A được gọi là tập con của tập B , nếu mọi phần tử của A đều là của B.

A  B  (xA  xB)

Cách viết khác nhau về tập con:

A  B - Đọc là : A là tập con của tập B, A nằm trong B;

B  A - Đọc là : B chứa A , B bao hàm A.

Như vậy, nếu A = B thì A là tập con của tập B và B cũng là tập con của tập A.

Thí dụ 1.8 Cho C ={ 1, 2, 5} và D={ 1,2,3,4,5} ta thấy C  D.

Tập tất cả các tập con của tập A gọi là tập 2A.

Thí dụ 1.9 Nếu A={ 1,2,3} thì 2A ={, {1},{2},{3}, {1,2},{1,3},{2.3},{1,2,3} }

Dễ dàng chứng minh được: Nếu A có n phần tử thì 2A có 2n phần tử (!).

Để mô tả mối quan hệ của 2 tập hợp người ta thường dùng sơ đồ Ven. Chẳng hạn, mô tả quan

hệ A  B bằng sơ đồ:

A B

1.2.3 Các phép toán trên tập hợp

a) Phép giao  : AB = { x | xA và xB}

b) Phép hợp  : AB = { x | xA hoặc xB}

c) Phép trừ - : A-B = A\B = { x | xA và xB}

d) Tập phần bù : Giả sử A là tập con U. Phần bù của tập A trong U là tập

Ac hay

= {xU | xA} =U-A

Nếu A là một tập "vũ trụ", nghĩa là mọi tập cần xét đều được xem là tập con của U, thì có thể

nói gọn lại Ac là phần bù của tập A.

Thí dụ 1.10 Cho A ={1,2,3,4,9} B = { 3,4,5,8} U ={0,1,2,3,4,5,6,7,8,9}.

Khi đó AB = {1,2,3,4,5,8,9} AB = {3,4 } A-B = {2,9} Ac = {0,5,6,7,8}

1.2.4 Tính chất của các phép toán tập hợp

a) Kết hợp : (AB)C = A(BC) (AB)C = AB(C)

b) Giao hoán : AB = BA B = BA

c) Phân phối : (AB) C = ( AC)(BC) (AB) C = (AC)  (BC)

d) Hai lần bù : (Ac)c =A

e) Luật DeMorgan: (AB)c = Ac  Bc ) (AB)c = Ac  Bc

1.2.5 Tích Des Cartes

Giả sử A, B , C là các tập hợp và {Ai}i=1,2,…,n là một họ n tập hợp. Khi đó ký hiệu:

AB = {(x,y)| xA và yB}

ABC = {(x,y,z)| xA, yB và zC }

AA A





 = {(x1,x2 ,…,xn)| xiAi ; i=1,2,…,n }

xi gọi là tọa độ thứ i của phần tử (x1,x2 ,…,xn)

Trường hợp riêng, nếu 12 n

AAA thì :

An = {(x1,x2 ,…,xn)| xiA ; i=1,2,…,n }

Dễ dàng chứng minh được : N(A1A2…An) =

()





1.2.6 Phủ và phân hoạch

Cho S là là một họ các tập con của tập A : S = (Ai), i=1,2,...,n. Khi đó S được gọi là một phân

phủ của tập A nếu



Nếu S là một phủ của A và tập Ai rời nhau từng đôi một thì S gọi là một phân hoạch của A.

Thí dụ 1.11 Ba tập













|0, |0, 0A x Rx B x Rx C     là một phân hoạch của tập R.

1.3 ÁNH XẠ

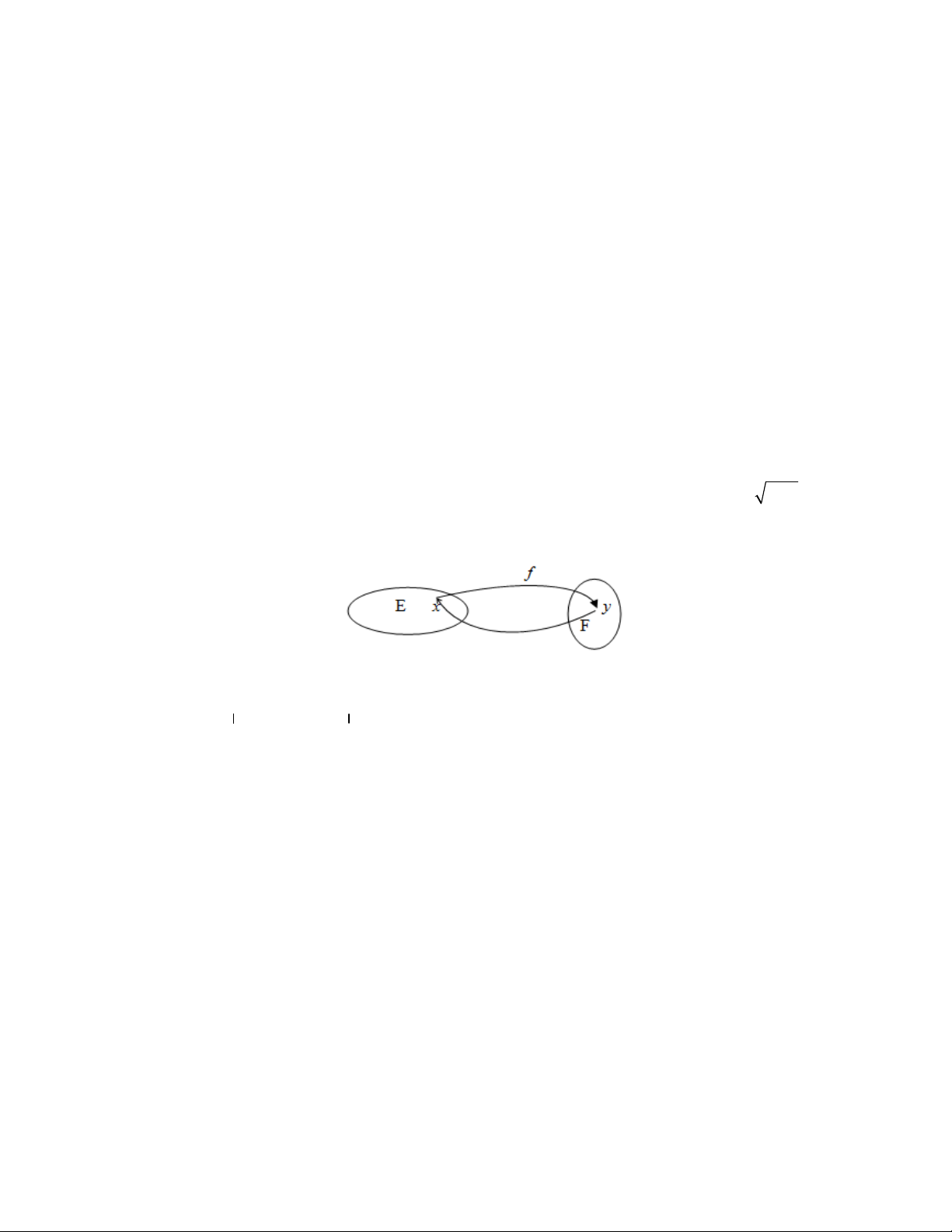
1.3.1 Khái niệm về ánh xạ: Ánh xạ từ tập E đến tập F là 1 qui luật f, liên hệ giữa E và F, sao cho khi

nó tác động vào 1 phần tử x thuộc tập E sẽ sinh ra 1 và chỉ 1 phần tử thuộc tập F.

Ký hiệu :

EF hay f





Gọi E là Tập nguồn và F là tập đích.

Nếu f tác động vào

E sinh ra yF



thì ta viết ()yfx



hay

Thí dụ 1.12 Một số ánh xạ : 31yx



 với EFR



;

[]yx



với ,ERFZ



;

sin2yx



 với EFR



.

Cho tập sinh viên lớp E và tập chỗ ngồi trong phòng học F, ()

x là chỗ ngồi của sinh viên x.

1.3.2 Tập ảnh: Giả sử :

EF, khi đó

- Tập ảnh của ánh xạ f là: () { | : ()}

EyFxEyfx



 

- Tập ảnh của tập

E qua ánh xạ f là: () { | : ()}

AyFxAyfx



 

1.3.3 Đơn ánh: Ánh xạ :

EF được gọi là một đơn ánh nếu từ 12 1 2

() ()

xfxfx



hay từ

1212

() ()

xfx xx.

1.3.4 Toàn ánh: Ánh xạ :

EF được gọi là một là một toàn ánh (ánh xạ tràn) nếu () .



1.3.5 Song ánh: Ánh xạ :

EF được gọi là một song ánh nếu nó vừa là đơn ánh vừa là toàn ánh.

Thí dụ 1.13 Xét các ánh xạ:

31yx với EFR: Là đơn ánh, toàn ánh nên là một song ánh.

[]yx với ,ERFZ

: Là toàn ánh , không đơn ánh.

sin 2yx với EFR: Không đơn ánh, không toàn ánh.

1.3.6 Ánh xạ ngược của song ánh: Cho song ánh :

EF khi đó tồn tại một ánh xạ :

FE

được xác định như sau ()

gy nếu ()yfx



. Ánh xạ ngược của ánh xạ f thường ký hiệu là 1



Thí dụ 1.14 Ánh xạ 31yx với EFR



 là một song ánh. Do đó: 13

() 1

fy y





Dễ dàng thấy rằng nếu f là song ánh thì 1



cũng là một song ánh và







Song ánh :

EF tạo ra một quan hệ 1-1 giữa 2 tập E và F

1.3.7 Hợp (tích) của hai ánh xạ

Cho :

EF và :

FG. Tích của hai ánh xạ f và g, ký hiệu 0:

fE G , được xác định

như sau: ( ) ( )

Eyfx zgy  . Nói các khác 0() [()]zgfx gfx



.

Thí dụ 1.15 Giả sử :sin()

yx và : log( )



thì 0: log(sin )

fz x



 Các tính chất (tự CM).

- Hợp của hai đơn ánh là đơn ánh;

- Hợp của hai toàn ánh là toàn ánh.

- Hợp của hai song ánh là song ánh.

Giả sử :

EF là song ánh thì 1



cũng là một song ánh. Khi đó





() () [()] ;

EI x f f x f fx x



    : IE là ánh xạ đồng nhất trên E.

Tương tự,





() ()

yFIy ff y y



  : IF là ánh xạ đồng nhất trên F.

ĐỀ CƯƠNG BÀI GIẢNG

Học phần: ĐẠI SỐ & HÌNH HỌC GIẢI TÍCH Đơn vị: Bộ môn Toán, Khoa CNTT

Thời gian: Tuần 2 Tiết 5-8

GV giảng 4, HV tự học: 4

Giáo viên: Nguyễn Trọng Toàn

Chương 1 TẬP HỢP VÀ ÁNH XẠ

Các mục

1.4 Luật hợp thành trong

1.5 Sơ lược về cầu trúc đại số

1.6 Số phức

Mục đích -

yêu cầu

- Giới thiệu sơ lược về các cấu trúc đại số: Nhóm, vành, trường.

- Nắm được khái niệm trường số phức C một số ứng dụng của nó.

NỘI DUNG

I. LÝ THUYẾT

1.4 LUẬT HỢP THÀNH TRONG

1.4.1 Định nghĩa: Luật hợp thành trong trên tập E, hay phép toán trên E là một quy luật tác động lên

hai phần tử của E sẽ tạo ra một và chỉ một phần tử của nó.

EE E , ( , )

yE z fxy E  . Thường ký hiệu: *zxy.

Thí dụ 1.16 - Luật cộng trong N : +

- Luật nhân trong R : ×

- Luật chia trong R-{0}: /

1.4.2 Tính chất. Giả sử * là một luật hợp thành trong trên tập E. Khi đó:

a) Giao hoán: Luật * gọi là có tính chất giao hoán nếu,**

yE xy yx



 

b) Kết hợp: Luật * gọi là có tính chất kết hợp nếu

,, (*)* *(*)

yz E x y z x y z 

c) Có phần tử trung hòa: Luật * gọi là có phần tử trung hòa e nếu

**eExE xeexx    

d) Phần tử đối xứng: Giả sử Luật * gọi là có phần tử trung hòa e . Phần tử

E gọi là có phần

tử đối xứng là '

nếu ' : x*''*

Exxxe  

Thí dụ 1.17

- Luật + trên N có tính chất giao hoán, kết hợp, có phần tử trung hòa là 0 và chỉ có phần tử 0

mới có phần tử đối xứng.

- Luật × trên Q hay R có tính chất giao hoán, kết hợp, có phần tử trung hòa là 1 và mọi phần tử

khác 0 đều có phần tử đối xứng.

1.5 SƠ LƯỢC VỀ CẤU TRÚC ĐẠI SỐ

Trên một tập hợp ta có thể trang bị một hay nhiều phép toán với một số tính chất xác định tạo ra

một đố tượng toán học gọi là cấu trúc đại số.

1.5.1 Cấu trúc nhóm. Giả sử tập G



 có trang bị một phép toán *. Khi đó (G,*) gọi là có cấu trúc

nhóm, gọi tắt là nhóm G, nếu thỏa các tính chất:

a) Luật * có tính kết hợp;

b) Luật * có phần tử trung hòa, ký hiệu e;

c) Mọi phần tử của G đều có phần tử đối;

d) Nếu luật * có tính chất giao hoán thì G gọi là một nhóm Abel.

Thí dụ 1.18 (Z,+) và (R-{0},×) là các nhóm Abel,

(R,×) không phải là nhóm.

 Một số tính chất của nhóm. Giả sử (G,*) là một nhóm, khi đó:

i) Phần tử trung hòa là duy nhất;

ii) Mỗi một phần tử của aG có một phần tử đối duy nhất a’;

iii) Trên nhóm G có quy tắc giản ước: * *ax ay x y



;

iv) Trên nhóm G phương trình *ax b



có nghiệm duy nhất '*



Đề cương bài giảng môn Đại số và Hình học giải tích

Chủ đề:

Tài liệu liên quan

Tài liêu mới

AI tóm tắt

Giới thiệu tài liệu

Đối tượng sử dụng

Từ khoá chính

Nội dung tóm tắt

Hỗ trợ

Phương thức thanh toán

Theo dõi chúng tôi