www.truongthi.com.vn Lớp học qua mạng
VẬT LÝ HẠT NHÂN
BÀI 4
GIẢI CÁC BÀI TOÁN HẠT NHÂN VÀ ĐỀ THI MẪU
A. GIẢI CÁC ĐỀ TOÁN
9. 1) Đây là câu hỏi giáo khoa, đề nghị các em tham khảo sách Giáo khoa để có lời giải đáp.
2) Ta có công thức : ⇒
0
λt
) = H .e-0
t
H
H= eλt ⇒ λt = ln( 0
t
H
H) ⇒ t = 1
λ
ln( 0
t
H
H) H(t
Với ln(2)
T
λ
= ⇒ t = T
ln(2) ln( 0
t
H
H) vì H0 = 4.H ⇒ t = 11200 năm
10. 1) Phản ứng phóng xạ α của pôlôni :
210 4 A
Z
84 2
Po He + X →
Cân bằng phản ứng, tính được : Z = 82 và A = 206, hạt nhân X sinh ra là chì 206 .
82 Pb
Năng lượng toả ra từ phản ứng : ∆E = (M0 – M)c2 = [(mPo – (mα + mX)]c2 = [209,93730 –
(4,00150 + 205,92944)].931 = 5,92 MeV
2) Số hạt α đượpc tạo thành bằng với số hạt Po đã bị phân rã, ta nhận thấy t = 276 = 2T,
như vậy sau thời gian t, tức là sau hai lần chu kỳ bán rã, số nguyên tử còn lại chỉ bằng
2
1
2= 1
4 số nguyên tử ban đầu.
3) Số phân tử đã bị phân rã là : ∆N = N0 – N = 3
4N0 . (Cũng có thể giải bằng công thức N
= N0.e–λt )
Với N0 là số hạt nhân ban đầu có trong 2,1g Po : N0 = 2,1.NA/210 = 2,1.6,02.1023 /210 =
6,02.1021 hạt ∆N = 0,75.6,02.1021 = 4,515.1021 hạt
Áp dụng định luật bảo toàn động lượng : Pb Pb
αα Po Po
m.v + m .v = m .v 0=
r
rr
mα.vα = mPb.vPb
Môn Vật lý Th ầy giáo Nguy ễn Thành Tương
Trường Chuyên Lê Hồng Phong - HCM
www.truongthi.com.vn Lớp học qua mạng
Động năng của các hạt cho bởi : Kα = 1
2mα.vα2 và KPb = 1
2mPb.vPb2
Suy ra : α
ααPb αPb Pb
αα
Pb Pb Pb Pb
mKK
Kv K
Kv m m mmm
+
== ⇒==+α
K
Động năng của hạt α là : Kα = Pb
αPb
m
m + m (Kα + KPb)
Mặt khác, năng lượng phản ứng toả ra bằng tổng động năng của các hạt : Kα + KPb = E =
5,92 MeV.
Tính được : Kα = 5,8 MeV
11. 1) Đây là một câu hỏi Giáo khoa, đề nghị các em đọc lại trong sách Vật Lý 12.
2) a. Phương trình phản ứng :
17
13
A A
ZZ
HLi X + X+→
Áp dụng định luật bảo toàn số A và số Z : 2.A = 1 + 7 = 8 ⇒ A = 4; 2.Z = 1 + 3 = 4 ⇒ Z = 2
Hạt nhân sinh ra là hạt nhân hêli . Phương trình viết dưới dạng hoàn chỉnh là :
He
4
2
17
13
4 4
2 2
H Li He + He+→
b. Ta có : M0 = mp + mLi = (1,0073 + 7,0140) = 8,0213u
M = 2.mHe = 2.4,0015u = 8,0030u
Vì M < M0 nên phản ứng toả năng lượng. Năng lượng toả ra là :
∆E = (M0 – M).c2 = (8,0213 – 8,0030).931 = 17,04 MeV
Năng lượng toả ra chỉ phụ thuộc vào hiệu (M0 – M), tức là phụ thuộc độ hụt khối của các hạt
nhân và không phụ thuộc vào động năng của prôtôn.
c. Áp dụng định luật bảo toàn năng lượng : M0.c2 + Kp = Mc2 + 2.KHe
Suy ra động năng của hạt X (tức là hạt He) là :
2
0
He
p
(M M)c +K
K2
−
= = 9,12 MeV
12. 1) Phương trình phản ứng : 17
13
4 4
2 2
H Li He + He+→
Môn Vật lý Th ầy giáo Nguy ễn Thành Tương
Trường Chuyên Lê Hồng Phong - HCM
www.truongthi.com.vn Lớp học qua mạng
Ta có : M0 = mp + mLi = (1,0073 + 7,0144) = 8,0217u
M = 2.mHe = 2.4,0015u = 8,0030u
Vì M < M0 nên phản ứng toả năng lượng. Năng lượng toả ra là :
∆E = (M0 – M).c2 = (8,0217 – 8,0030).931 = 17,4 MeV
2) Hai hạt được tạo ra đều là hêli, gọi KHe là động năng của mỗi hạt, ta có :
2
0
He
p
(M M)c +K
K2
−
= = 9,2 MeV
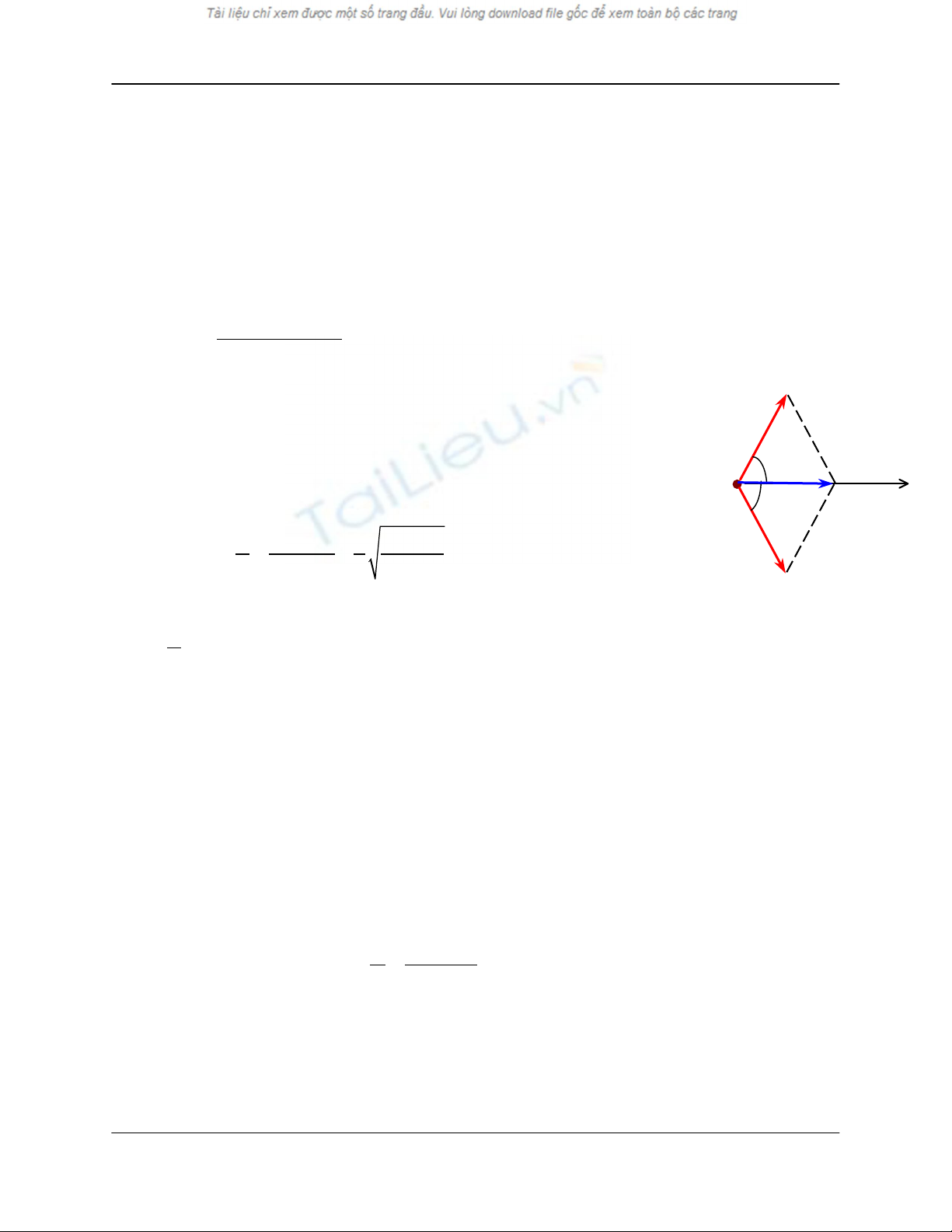
3) Áp dụng định luật bảo toàn động lượng : X2
p
p
X1
m .v + m .v = m .v
r
rr
ϕ
/2
ϕ
/2
p
p
mv
r
X2
mv
X1
mv
r
Chiếu xuống phương chuyển động của prôtôn :
2.mXv1.cos(ϕ/2) = mpvp với ϕ là góc họp bởi phương các vectơ
vận tốc của hai hạt.
Tính được :
XX XX
ppp p
m.v 2m.K
1
cos 2 2.m .v 2 2m K
ϕ
== = 0,0824
2
ϕ
= 85,27o ⇒ ϕ = 171o
13. 1) Ta có : ∆E = ∆M.c2 = (mU + mn – mMo – mLa – 2.mn ).c2 = (mU – mn – mMo – mLa).c2
= ( 234,99 – 1,01 – 94,88 – 138,87).931 = 214,13 MeV = 3,43.10–11 J
2) Số hạt nhân có trong 1g 235U là : N = m.NA/235 = 6,023.1023 /235 = 2,56.1021 hạt
Một gam 235U khi phân hạch hết sẽ toả ra năng lượng bằng : E = N.∆E =
2,56.1021.3,43.10–11 = 8,78.1010 J
4) Để có được năng lượng tương đương với năng lượng trên, khối lượng than phải
sử dụng là M =
10
3
7
E 8,78.10 3.10 kg = 3
Q 2,97.10
=≈ tấn
Môn Vật lý Th ầy giáo Nguy ễn Thành Tương
Trường Chuyên Lê Hồng Phong - HCM
www.truongthi.com.vn Lớp học qua mạng
A. GIẢI ĐỀ THI MẪU
Câu 1 1) Sóng từ nguồn A truyền đến M mất thời gian θ = 1
d
v, nên biểu thức sóng khi
đến M sẽ là : u1 = a.sinω(t – 1
d
v) = a.sin(ωt –ω1
d
v) = a.sin(ωt – 1
2πfd
v)
Vì λ = v/f nên có thể viết : 1
1
2πd
u = a.sin t
ωλ

−


Tương tự, sóng từ nguồn B khi truyền đến M có biểu thức : 2
2
2πd
u = a.sin t
ωλ

−


Phương trình sóng tổng hợp tại M là : u
M = u1 + u2 = 1
2πd
a.sin t
ωλ

−


+
2
2πd
a.sin t
ωλ
−

uM = 2a.cos 21
π(d d )
λ
−12
π(d d
sin t
ωλ
+

−


2) Tại những điểm có biên độ cực đại, ta có :
cos 21
π(d d )
λ
− = ± 1 ⇒ 21
π(d d )
λ
− = k.π ⇒ (d2 – d1) = k.λ
Những điểm có biên độ cực đại nằm trên những nhánh hyperbol nhận A và B làm tiêu
điểm (kể cả đường trung trực của AB).
3) Pha ban đầu tại M có giá trị phụ thuộc vào dấu của cos 21
π(d d )
λ
−.
• Nếu cos 21
π(d d )
λ
−> 0 thì ϕ = – 12
π(d d )
λ
+
• Nếu cos 21
π(d d )
λ
−< 0 thì ϕ = π – 12
π(d d )
λ
+
Những điểm có tổng d1 + d2 bằng nhau sẽ nằm trên những đường ellip nhận A và B làm tiêu
điểm. Vì lý do đã nêu trên, những điểm đó sẽ tạo thành hai tập hợp dao động có pha ngược
Môn Vật lý Th ầy giáo Nguy ễn Thành Tương
Trường Chuyên Lê Hồng Phong - HCM
www.truongthi.com.vn Lớp học qua mạng
nhau. Suy ra quỹ tích những điểm dao động cùng pha sẽ nằm trên những cung cách đoạn trên
đường ellip đó.
Câu II Trong tế bào quang điện, phôtôn có năng lượng thích hợp khi chiếu tới tấm kim loại sẽ
làm bật êlectrôn quang điện ra khỏi kim loại đó. Trong ống phóng tia Rơnghen, êlectrôn xuất
phát từ catôt sau khi được tăng tốc sẽ tới đập vào đối catôt làm phát sinh ra các phôtôn tia
Rơnghen từ đây.
Trong tế bào quang điện hiệu điện thế UAK giữa hai cực thường có giá trị nhỏ (vài vôn tới vài
chục vôn), nếu UAK dương thì electrôn sẽ được tăng tốc khi đến anôt ,nếu UAK âm thì tới một giá
trị nhất định (Uh) nó sẽ làm triệt tiêu dòng quang điện.
Trong ống phóng tia Rơnghen, hiệu điện thế UAK giữa hai cực luôn luôn dương và có giá trị rất
cao (tới hàng trăm nghìn vôn), độ lớn của U ảnh hưởng tới bước sóng của phôtôn tia Rơnghen
phát ra (U càng cao thì λ càng ngắn)
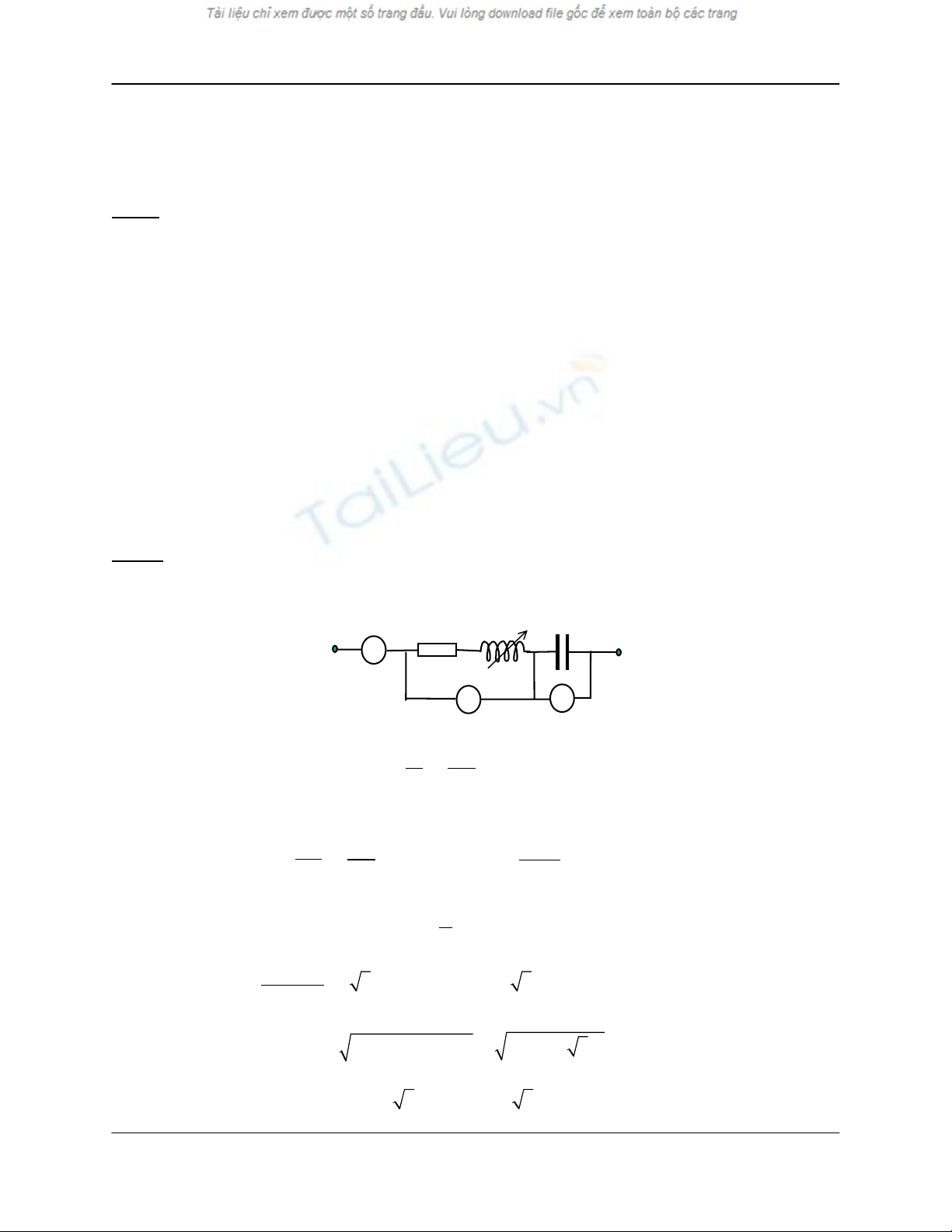
Câu III
R L C
A M B
V2
V
A
A. 1) Tổng trở của toàn mạch : U
I
=Z = 100 = 200 Ω
0,5
Dung kháng : C
2
U
ZI
= = 100
0,5 = 200 Ω ⇒ C =
C
1
Z.ω = 15,9.10–6 F = 15,9 µF
Hiệu điện thế sớm pha hơn dòng điện góc π
3 nên ta có :
LC
ZZ
tg R
ϕ
−
= = 3 ⇒ (ZL – ZC) = R 3 (1)
Tổng trở có biểu thức : 22
LC
R(ZZ)Z=+− = 2
R(R3)+2
=2R = 200 ⇒ R = 100Ω
Thay vào (1) tính được : ZL = ZC + R 3= 200 + 100 3 = 373 Ω ⇒ L = 373/100π = 1,19H
Môn Vật lý Th ầy giáo Nguy ễn Thành Tương
Trường Chuyên Lê Hồng Phong - HCM