Giáo trình thuỷ khí
Lớp biên
Chương lớp biên
Đặt vấn đề
Vấn đề quan trọng trong cơ học chất lỏng ứng dụng là
tính lực cản của vật chuyển động trong chất lỏng
(hoặc vật đứng yên còn chất lỏng chuyển động bao
quanh). Ví dụ: Khảo sát tàu thuỷ chuyển động trên mặt
nước, máy bay chuyển động trong chất lỏng với vận tốc
không đổi. Khi đó công suất động cơ dùng để khắc phục
lực cản. muốn biết lực cản phải biết phân bố lực ma
sát (ứng suất tiếp) trên bề mặt của vật tiếp xúc với
chất lỏng, do đó phải nghiên cứu lớp chất lỏng sát
vật: lớp biên. Trong lớp chất lỏng này tính nhớt đóng
vai trò rất quan trọng, ở sát bề mặt vật vận tốc của
chất lỏng bằng 0 và vận tốc này sẽ tăng rất nhanh để
đạt giá trị bằng vận tốc ở vùng ngoài lớp biên, vì
vậy trong vùng lớp biên, gradient vận tốc có giá trị
rất lớn.
1. Khái niệm về lớp biên. các chiều dày đặc trưng
của lớp biên
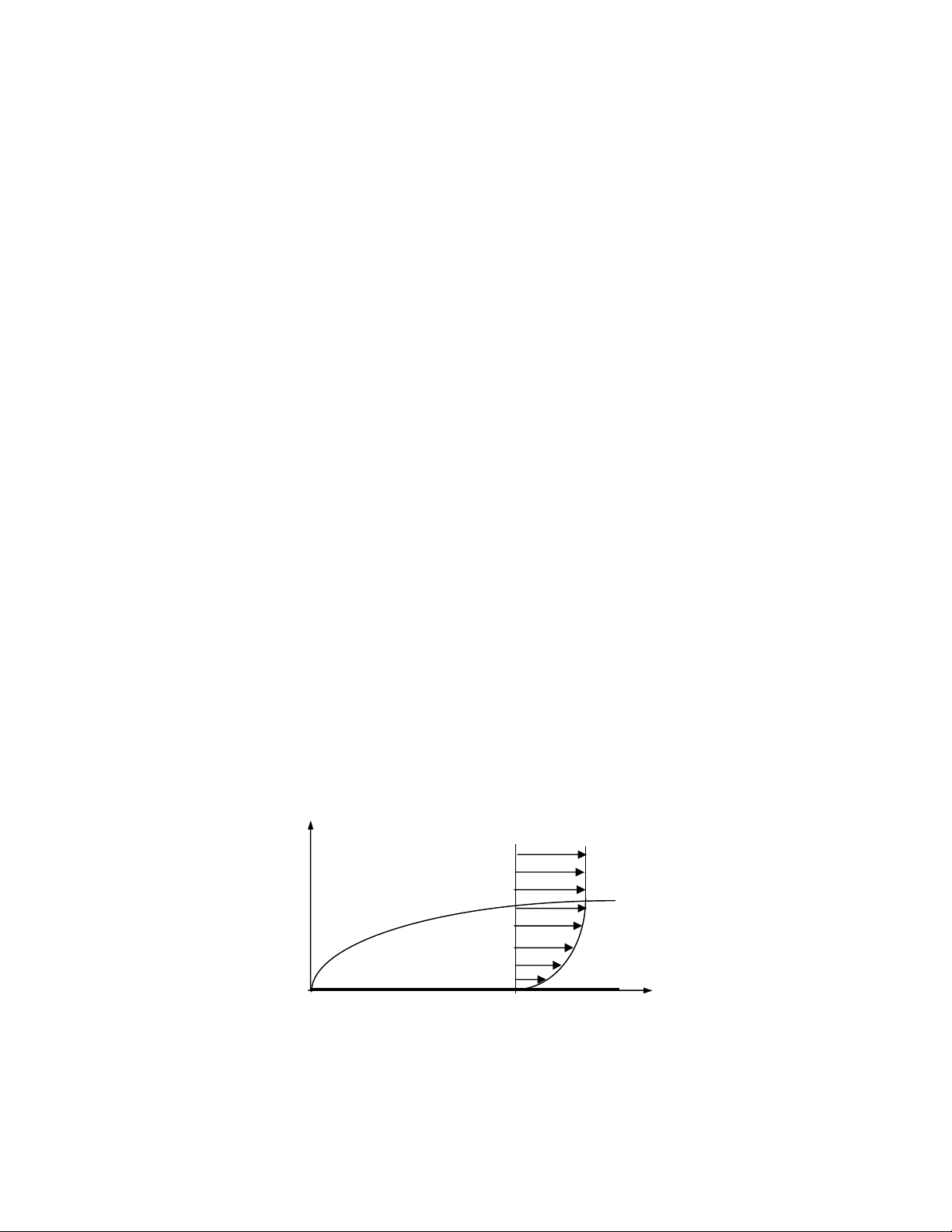
I. Lớp biên
Khảo sát 1 bản phẳng đứng yên, trên bản phẳng có dòng
chất lỏng chuyển động với vận tốc u. Trên bề mặt bản
x
y
phẳng do tính bám của chất lỏng nên vận tốc lớp chất
lỏng trên bề mặt là u=0, các lớp chất lỏng tiếp đó có
vận tốc tăng dần cho đến lúc vận tốc đạt giá trị u
của dòng, nghĩa là có sự chuyển hoá từ u=0 u= u.
Định nghĩa: Lớp chất lỏng từ bề mặt vật có vận tốc
u=0 cho đến vị trí có vận tốc bằng 99% u gọi là lớp
biên.
Gọi là khoảng cách từ từ bề mặt vật đến vị trí có
vận tốc bằng 99% u: chiều dày lớp biên, gia trị
const trong lớp biên: =(x)
Nhận xét:
Trong chiều dày lớp biên, sự thay đổi vận tốc diễn
ra rất nhanh: dy
du lớn do đó ứng suất tiếp dy
du
là
rất lớn: ta khảo sát với giả thuyết chất lỏng là
thực.
Ngoài lớp biên dy
du 0 =0, ảnh hưởng của tính nhớt
không đáng kể, ta có thể coi chất lỏng là lý tưởng.
II. Các chiều dày đặc trưng của lớp biên:
Khái niệm về chiều dày lớp biên không có ý nghĩa định
lượng chính xác, khi y tăng vận tốc của lớp biên tiến
dần đến giá trị của dòng ngoài u. Đại lượng phụ
thuộc vào việc chọn ở đâu điểm quy ước rõ biên giới
lớp biên. Do đó người ta đưa ra những chiều dày đặc
trưng khác của lớp biên.
1) Chiều dày bị ép:
*
y
u
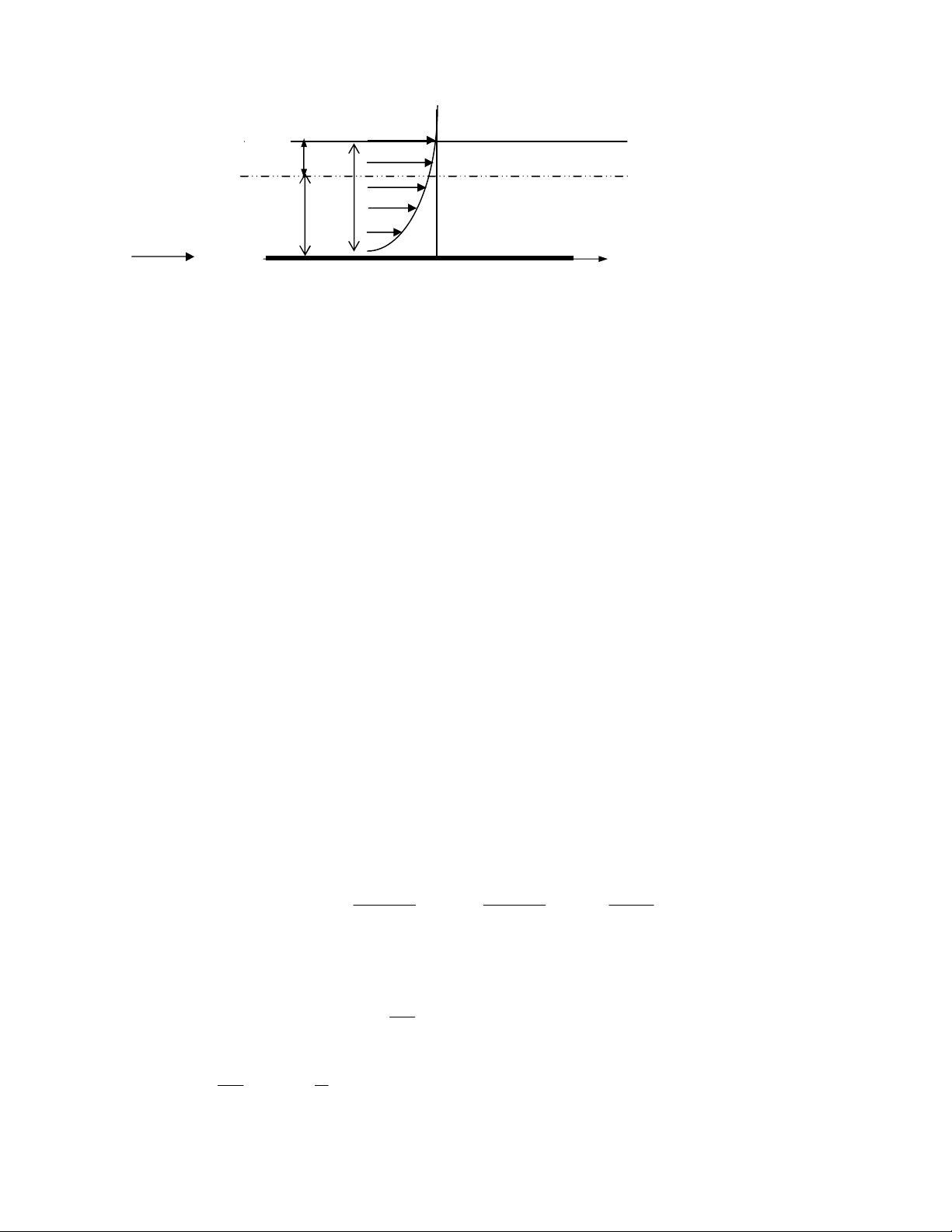
Xét ảnh hưởng động học của tính nhớt lên vị trí đường
dòng. Vì đường dòng là đường lưu lượng bằng nhau nên
đường dòng AB trong chất lỏng lý tưởng phải tương ứng
với đường dòng A’B’ trong chất lỏng thực nhưng ở xa
bề mặt vật hơn. Gọi * là khoảng cách dịch chuyển của
đường dòng do ảnh hưởng của tính nhớt, ta tính lưu
lượng Qt của chất lỏng thực qua mặt cắt giữa bề mặt
vật và đường dòng cách thành rắn một khoảng y (xét
trên bề rộng vật bằng 1 đơn vị):
0
tdyuQ
Đường dòng tương ứng của chất lỏng lý tưởng sẽ gần bề
mặt vật hơn 1 đoạn *, tính từ điều kiện cân bằng lưu
lượng:
0
t
*
ldyuQuQ
0
0
0
0
*dy
u
u
1
u
dyu
dy
u
dyu
Đối với chất lỏng không nén thì ==const
dy
u
u
1
0
*
(1)
Đặt
ddyy
y
u
u
lý
ự
c
AB
A'
*
Vậy
d1dy1dy
u
u
1
1
000
*
d1
1
0
* (1')
* là chiều dày bị ép, đặc trưng cho sự lệch dòng do
có lớp biên, ngoài ra * còn đặc trưng cho sự giảm lưu
lượng của dòng chảy qua mặt cắt với thành rắn của
vật. Sự giảm lưu lượng đó do lớp biên ép chất lỏng
làm chất lỏng chuyển động trong lớp biên có vận tốc
nhỏ hơn vận tốc u
của dòng ngoài.
Với lớp biên trên tấm phẳng, chất lỏng không nén: * =
0,375.
2) Chiều dày mất xung lực
**
Xét ảnh hưởng động lực của tính nhớt lên dòng chảy
bao quanh vật.
Xét động lượng tiêu hao trong lớp biên có bề rộng
bằng 1 đơn vị trong 1 đơn vị thời gian
dyuuuuudyuuudQdK
000
Gọi **: chiều dày mất xung lực, là đại lượng thoả mãn
biểu thức:
dKdyuuuuu
0
**