M C L CỤ Ụ
Th tứ ự N i dungộTrang
1 M c l cụ ụ 1
2 Ph n A: M đuầ ở ầ 1
3 I. Lí do ch n đ tàiọ ề 1
4 II. M c đích, nhi m v nghiên c uụ ệ ụ ứ 2
5 III. Ph m vi và đi t ng nghiên c uạ ố ượ ứ 2
6 IV. Ph ng pháp nghiên c uươ ứ 2
7 Ph n B: N I DUNGầ Ộ 2
8 I. C s lý lu nơ ở ậ 3
9 II. Th c tr ng c a v n đự ạ ủ ấ ề 3
10 III. Gi i pháp và t ch c th c hi nả ổ ứ ự ệ 3
11 1. Ph ng pháp gi iươ ả 4
12 2. Ví d minh h aụ ọ 4
13 3. Bài t p t ng tậ ươ ự 15
14 IV. K t qu đt đcế ả ạ ượ 16
15 Ph n C: K T LU N VÀ KI N NGHầ Ế Ậ Ế Ị 17
16 Tài li u tham kh oệ ả 18
1

PH N A: M ĐUẦ Ở Ầ
1. LÍ DO CH N Đ TÀI.Ọ Ề
Đng ta quan ni m “Hi n tài là nguyên khí qu c gia’’ và đc bi tả ệ ề ố ặ ệ
coi tr ng vi c b i d ng nhân tài cho đt n c. B giáo d c và đào t o cũngọ ệ ồ ưỡ ấ ướ ộ ụ ạ
có nh ng chú tr ng đc bi t trong công tác b i d ng h c sinh gi i các c p.ữ ọ ặ ệ ồ ưỡ ọ ỏ ấ
Đó là ti p t c xây d ng và phát tri n các tr ng chuyên toàn di n h n,ế ụ ự ể ườ ệ ơ
khuy n khích và tôn vinh các h c sinh xu t s c đt thành tích cao trong các kế ọ ấ ắ ạ ỳ
thi h c sinh gi i trong n c và qu c t . V n d ng cách d y h c phân hóaọ ỏ ướ ố ế ậ ụ ạ ọ
trong công tác b i d ng h c sinh gi i. Các tr ng chuyên có th xây d ngồ ưỡ ọ ỏ ườ ể ự
phân ph i ch ng trình riêng phù h p v i khă năng c a h c sinh…ố ươ ợ ớ ủ ọ
Trong quá trình gi ng d y và b i d ng môn toán cho h c sinhả ạ ồ ưỡ ọ
gi i, m c tiêu chính c a ng i d y là giúp vi c h c t p nh ng ki n th c vỏ ụ ủ ườ ạ ệ ọ ậ ữ ế ứ ề
lý thuy t, hi u và v n d ng vào bài t p và cao h n là ng d ng vào khoa h cế ể ậ ụ ậ ơ ứ ụ ọ
cu c s ng.ộ ố
Bài t p toán h c trong ch ng trình ph thông r t đa d ng và cóậ ọ ươ ổ ấ ạ
nh ng ph n khó, đc bi t là các bài toán trong đ thi h c sinh gi i t nh, qu cữ ầ ặ ệ ề ọ ỏ ỉ ố
gia hàng năm r t khó và đa d ng v ph n.ấ ạ ề ầ
Nh chúng ta đã bi t trong các đ thi h c sinh gi i ho c đ thiư ế ề ọ ỏ ặ ề
đi h c th ng có m t bài toán v PT – BPT – HPT – HBPT ch a tham s ,ạ ọ ườ ộ ề ứ ố
đây th ng là m t câu h i khó trong đ thi. Thông th ng h c sinh khi g pườ ộ ỏ ề ườ ọ ặ
câu h i này th ng lúng túng khi đnh h ng l i gi i.ỏ ườ ị ướ ờ ả
V v n đ này, cũng đã có r t nhi u tài li u, sáng ki n kinhề ấ ề ấ ề ệ ế
nghi m (SKKN). Tuy nhiên tài li u vi t chuyên sâu, ch ra các d ng toán đi nệ ệ ế ỉ ạ ể
hình thì ch a có. Chính vì v y tôi đã ti n hành nghiên c u đ tài ‘’H ng d nư ậ ế ứ ề ướ ẫ
h c sinh khá gi i gi i m t s d ng toán đi n hình v PT – BPT – HPT ch aọ ỏ ả ộ ố ạ ể ề ứ
tham s ’’, v i hy v ng có th đ giúp các em h c sinh có m t tài li u thamố ớ ọ ể ể ọ ộ ệ
kh o h u ích, giúp các em có đnh h ng chính xác khi gi i các bài toán PT –ả ữ ị ướ ả
BPT – HPT – HBPT ch a tham s .ứ ố
2. M C ĐÍCH, NHI M V NGHIÊN C U.Ụ Ệ Ụ Ứ
- Giúp h c sinh nh n d ng đc các PT, HPT, BPT, HBPT ch a thamọ ậ ạ ượ ứ
s ố
- B i d ng cho h c sinh v ph ng pháp, k năng gi i toán. Qua đóồ ưỡ ọ ề ươ ỹ ả
h c sinh nâng cao kh năng t duy, sáng t o. ọ ả ư ạ
- Nâng cao kh năng t h c, t b i d ng và kh năng gi i các bài toánả ự ọ ự ồ ưỡ ả ả
trong k thi tuy n sinh vào Đi h c và ôn luy n HSG môn Toán.ỳ ể ạ ọ ệ
3. ĐI T NG NGHIÊN C U.Ố ƯỢ Ứ
2

- Các d ng toán gi i PT, HPT, BPT, HBPT ch a tham s trong ch ngạ ả ứ ố ươ
trình toán ph thông, đc bi t là trong các k thi tuy n sinh vào Đi h c, trongổ ặ ệ ỳ ể ạ ọ
các k thi ch n HSG c p t nhỳ ọ ấ ỉ .
- Phân lo i các d ng toán th ng g p và ph ng pháp gi i m i d ngạ ạ ườ ặ ươ ả ỗ ạ .
4. PH NG PHÁP NGHIÊN C U.ƯƠ Ứ
Đ th c hi n m c đích và nhi m v c a đ tài, trong quá trình nghiênể ự ệ ụ ệ ụ ủ ề
c u tôi đã s d ng các ph ng pháp sau:ứ ử ụ ươ
- Nghiên c u các lo i tài li u s ph m, qu n lí có liên quan đn đ tài.ứ ạ ệ ư ạ ả ế ề
- Ph ng pháp quan sát (công vi c d y- h c c a giáo viên và HS).ươ ệ ạ ọ ủ
- Ph ng pháp đi u tra (nghiên c u ch ng trình, h s chuyên môn,ươ ề ứ ươ ồ ơ
…).
- Ph ng pháp đàm tho i ph ng v n (l y ý ki n c a giáo viên và HS ươ ạ ỏ ấ ấ ế ủ
thông qua trao đi tr c ti p).ổ ự ế
- Ph ng pháp th c nghi m.ươ ự ệ
PH N B: N I DUNG SKKNẦ Ộ
I. C S LÍ LU N:Ơ Ở Ậ
1. Lí lu n chung:ậ
Ch ng trình giáo d c ph thông ph i phát huy tính tích c c, t giác, chươ ụ ổ ả ự ự ủ
đng sáng t o c a h c sinh, phù h p v i đc tr ng môn h c, đc đi mộ ạ ủ ọ ợ ớ ặ ư ọ ặ ể
đi t ng h c sinh, đi u ki n c a t ng l p h c, b i d ng h c sinhố ượ ọ ề ệ ủ ừ ớ ọ ồ ưỡ ọ
ph ng pháp t h c, kh năng h p tác, rèn luy n k năng v n d ng ki nươ ự ọ ả ợ ệ ỹ ậ ụ ế
th c vào th c ti n, tác đng đn tình c m, đem l i ni m vui, h ng thú vàứ ự ễ ộ ế ả ạ ề ứ
trách nhi m h c t p cho h c sinh. ệ ọ ậ ọ
Quá trình d y h c v i các nhi m v c b n là hình thành tri th c, rènạ ọ ớ ệ ụ ơ ả ứ
luy n các k năng ho t đng nh n th c, hình thành thái đ tích c c...đcệ ỹ ạ ộ ậ ứ ộ ự ượ
xây d ng trên quá trình ho t đng th ng nh t gi a th y và trò, trò và trò, tínhự ạ ộ ố ấ ữ ầ
t giác, tích c c t ch c, t đi u khi n ho t đng h c nh m th c hi n t tự ự ổ ứ ự ề ể ạ ộ ọ ằ ự ệ ố
các nhi m v đã đc đ ra.ệ ụ ượ ề
2. Ki n th c v n d ng:ế ứ ậ ụ
a) Đnh nghĩa đo hàm, các quy t c tính đo hàm, các công th c tínhị ạ ắ ạ ứ
đo ạ
hàm c a các hàm s th ng g p, công th c tính đo hàm c a hàmủ ố ườ ặ ứ ạ ủ
h p.ợ
b) Đ gi i các PT, HPT, BPT, HBPT có ch a tham s b ng ph ngể ả ứ ố ằ ươ
pháp
đo hàm ta c n n m c n n m v ng các m nh đ sau:ạ ầ ắ ầ ắ ữ ệ ề
Cho hàm s ố
( )y f x=
liên t c trên t p ụ ậ
D
1: S nghi m c a ph ng trình ố ệ ủ ươ f(x)=g(x) b ng s giao đi m c a hai đằ ố ể ủ ồ
th ị
hàm s ốy=f(x) và y=g(x).
3

2: Ph ng trình ươ
( )f x m=
có nghi mệ
( ) ( )
min m ax
x D x D
x D f x m f x
��
3: BPT
( )f x m
có nghi m ệ
( )
min
x D
x D f x m
�
4: BPT
( )f x m
nghi m đúng v i m i ệ ớ ọ
( )
max
x D
x D f x m
�
5: BPT
( )f x m
có nghi m ệ
( )
max
x D
x D f x m
�۳
6: BPT
( )f x m
, nghi m đúng v i m i ệ ớ ọ
( )
min
x D
x D f x m
�۳
7: Cho hàm s ố
( )y f x=
đn đi u trên t p ơ ệ ậ
D
Khi đó
( ) ( )
f u f v u v= =�
(v i m i ớ ọ
,u v D
)
II. TH C TR NG V N Đ:Ự Ạ Ấ Ề
- Qua th c ti n h c t p và gi ng d y, b n thân nh n th y các PT, HPT,ự ễ ọ ậ ả ạ ả ậ ấ
BPT, HBPT ch a tham s th ng r t đa d ng và khó. Nên h c sinh th ngứ ố ườ ấ ạ ọ ườ
không m nh d n, t tin đ tìm l i gi i cho các bài toán này. Đc bi t tài li uạ ạ ự ể ờ ả ặ ệ ệ
chuyên sâu v d ng toán này ít, không ch rõ các d ng toán th ng g p, cácề ạ ỉ ạ ườ ặ
h ng đ thi có th ra.....ướ ề ể
III. GI I PHÁP VÀ T CH C TH C HI NẢ Ổ Ứ Ự Ệ
Trong th c ti n gi ng d y cho h c sinh, tác gi đã giúp h c sinh nh nự ễ ả ạ ọ ả ọ ậ
d ng bài toán và ph ng pháp gi i các d ng toán theo h th ng bài t p đcạ ươ ả ạ ệ ố ậ ượ
s p x p theo m t trình t logic.ắ ế ộ ự
1. Ph ng pháp gi i ươ ả
D ng toán th ng g p là tìm giá tr tham s m đ PT, BPT có nghi mạ ườ ặ ị ố ể ệ
(ho c có nghi m th a mãn đi u ki n nào đó). V i d ng toán này ta có thặ ệ ỏ ề ệ ớ ạ ể
th c hi n theo các b c nh sau:ự ệ ướ ư
B c 1: ướ Bi n đi PT, BPT v d ng ế ổ ề ạ
( ) ( )
f x g m=
(ho c ặ
( ) ( )
f x g m
,
ho c ặ
( ) ( )
f x g m
. Hay còn g i là cô l p ọ ậ m).
B c 2:ướ Tìm t p xác đnh ậ ị
D
c a hàm s ủ ố
( )
f x
B c 3: ướ Tính
( )
'f x
B c 4: ướ L p b ng bi n thiên c a hàm s ậ ả ế ủ ố
( )
f x
B c 5: ướ Xác đnh ị
( )
min
x D
f x
và
( )
max
x D
f x
T đó v n d ng m t trong các m nh đ đã nêu ph n ki n th c bên ừ ậ ụ ộ ệ ề ở ầ ế ứ
trên rút ra k t lu n cho bài toán.ế ậ
L u ý:ư Tr ng h p các PT, BPT ch a các bi u th c ph c t p, ta có ườ ợ ứ ể ứ ứ ạ
th xem xét đt n ph đ đn gi n chúng. N u đc ta làm nh sau:ể ặ ẩ ụ ể ơ ả ế ượ ư
Đt ặ
( )
t x
ϕ
=
(
)(x
là m t bi u th c trong PT, BPT)ộ ể ứ
T đi u ki n ràng bu c c a n s ừ ề ệ ộ ủ ẩ ố
Dx
, tìm đi u ki n c a n ề ệ ủ ẩ
s ố
t
, ví d ụ
Kt
(chú ý là ph i tìm đc đi u ki n ch t c a ả ượ ề ệ ặ ủ t)
Đa PT, BPT n s ư ẩ ố
x
v PT, BPT n s ề ẩ ố
t
ta đc ượ
( ) ( )
f t h m=
(ho c ặ
( ) ( )
f t h m
, ho c ặ
( ) ( )
f t h m
).
4
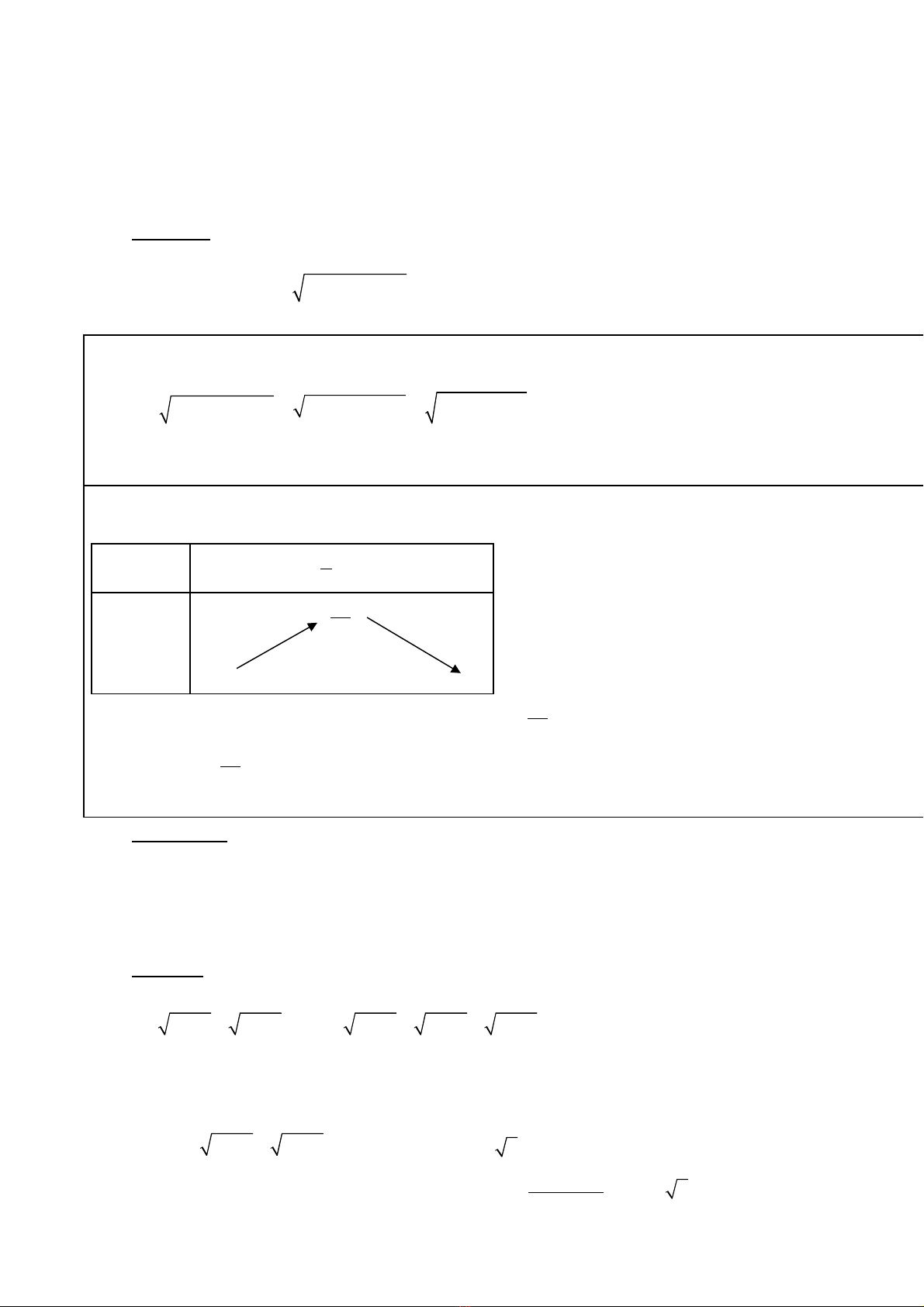
L p b ng bi n thiên c a hàm s ậ ả ế ủ ố
( )
f t
trên t p K.ậ
T b ng bi n thiên rút ra k t lu n bài toán.ừ ả ế ế ậ
2. Các d ng toán đi n hình.ạ ể
D ng 1: Tìm tham s đ ph ng trình có nghi m.ạ ố ể ươ ệ
Ví d 1:ụ Tìm m đ ph ng trình sau có nghi m:ể ươ ệ
( ) ( )
2
4 6 2x x x x m+ − + − =
L i gi i: ờ ả
Nh n xét:ậ
V i bài toán trên thì vi c đt n ph là thích h p, tuy nhiên các em nh ớ ệ ặ ẩ ụ ợ ớ
là ph i tìm đi u ki n chính xác c a n ph .ả ề ệ ủ ẩ ụ
Ví d 2ụ : Tìm tham s m đ ph ng trình. ố ể ươ
()
2 2 4 2 2
1 1 2 2 1 1 1m x x x x x+ − − + = − + + − −
có nghi m.ệ
L i gi i:ờ ả
ĐK
1 1x−
Đt ặ
( )
2 2
1 1 1 1t x x x= + − − −
0 2t�
( l p b ng bi n thiên)ậ ả ế
Khi đó ph ng trình đc đa v d ng ươ ượ ư ề ạ
( )
220 2
2
t t
m t
t
− + +
=
+
Đt ặ
( ) ( ) ( )
2
2
4 6 2 24 25 1 0 5t x x x x x t−− = + +− =− + =�
Ph ng trình tr thành:ươ ở
224t t m− + + =
;
[ ]
0;5t
Xét hàm s ố
( )
224f t t t= − + +
trên đo n ạ
5;0
Ta có b ng bi n thiên sau: ả ế
t
0
2
1
5
( )
f t
4
97
24 4
T đó suy ra ph ng trình có nghi m khi ừ ươ ệ
97
44
m
V y ậ
97
44
m
5





















