
SỞ GIÁO DỤC VÀ ĐÀO TẠO NGHỆ AN
SÁNG KIẾN KINH NGHIỆM
Đề tài:
RÈN LUYỆN TƯ DUY HỌC SINH KHỐI 12 THÔNG QUA KHAI
THÁC CÁC BÀI TOÁN CỰC TRỊ HÌNH HỌC KHÔNG GIAN OXYZ
LĨNH VỰC: MÔN TOÁN HỌC
Diễn Châu, tháng 04 năm 2022

SỞ GIÁO DỤC VÀ ĐÀO TẠO NGHỆ AN
TRƯỜNG THPT DIỄN CHÂU 3
SÁNG KIẾN KINH NGHIỆM
Đề tài:
RÈN LUYỆN TƯ DUY HỌC SINH KHỐI 12 THÔNG QUA KHAI
THÁC CÁC BÀI TOÁN CỰC TRỊ HÌNH HỌC KHÔNG GIAN OXYZ
LĨNH VỰC: MÔN TOÁN HỌC
Người thực hiện: NGUYỄN VĂN DŨNG
Tổ bộ môn: Toán - Tin
Điện thoại: 0349734147
Email: dungtoandhv@gmail.com
Diễn Châu, tháng 04 năm 2022

MỤC LỤC
Phần I. ĐẶT VẤN ĐỀ Trang 1
1. Lý do chọn đề tài Trang 1
2. Tính cấp thiết của đề tài Trang 2
3. Tính mới của đề tài Trang 2
4. Khả năng ứng dụng và triển khai đề tài Trang 2
5. Đối tượng và phạm vi nghiên cứu Trang 2
6. Phương pháp và nhiệm vụ nghiên cứu Trang 3
Phần II. NỘI DUNG Trang 3
1. Cơ sở khoa học Trang 3
1.1. Cơ sở lý luận Trang 3
1.2. Cơ sở thực tiến Trang 3
2. Thực trạng về các bài toán cực trị trong không gian Oxyz Trang 5
3. Phương hướng và giải pháp Trang 6
3.1. Bài toán cực trị về khoảng cách trong không gian Oxyz Trang 7
3.1.1. Giải pháp chung Trang 7
3.1.2. Ví dụ áp dụng Trang 9
3.1.3. Bài tập tham khảo Trang 23
3.2. Bài toán cực trị về góc trong không gian Oxyz Trang 24
3.2.1. Giải pháp chung Trang 24
3.2.2. Ví dụ áp dụng Trang 25
3.2.3. Bài tập tham khảo Trang 34
3.3. Bài toán cực trị về diện tích, thể tích trong không gian Oxyz Trang 35
3.3.1. Giải pháp chung Trang 35
3.3.2. Ví dụ áp dụng Trang 36
3.3.3. Bài tập tham khảo Trang 40
3.4. Bài toán cực trị khác trong không gian Oxyz Trang 41
3.4.1. Giải pháp chung Trang 42

3.4.2. Ví dụ áp dụng Trang 42
3.4.3. Bài tập tham khảo Trang 51
Phần III. KẾT LUẬN, KIẾN NGHỊ Trang 53
1. Kết luận về quá trình nghiên cứu Trang 53
1.1. Về quá trình nghiên cứu và triển khai Trang 53
1.2. Phân tích kết quả thực nghiệm Trang 57
1.3. Đánh giá kết quả thực nghiệm Trang 57
2. Ý nghĩa của đề tài Trang 57
3. Đề xuất và kiến nghị Trang 58
PHỤ LỤC Trang 59
TÀI LIỆU THAM KHẢO Trang 69
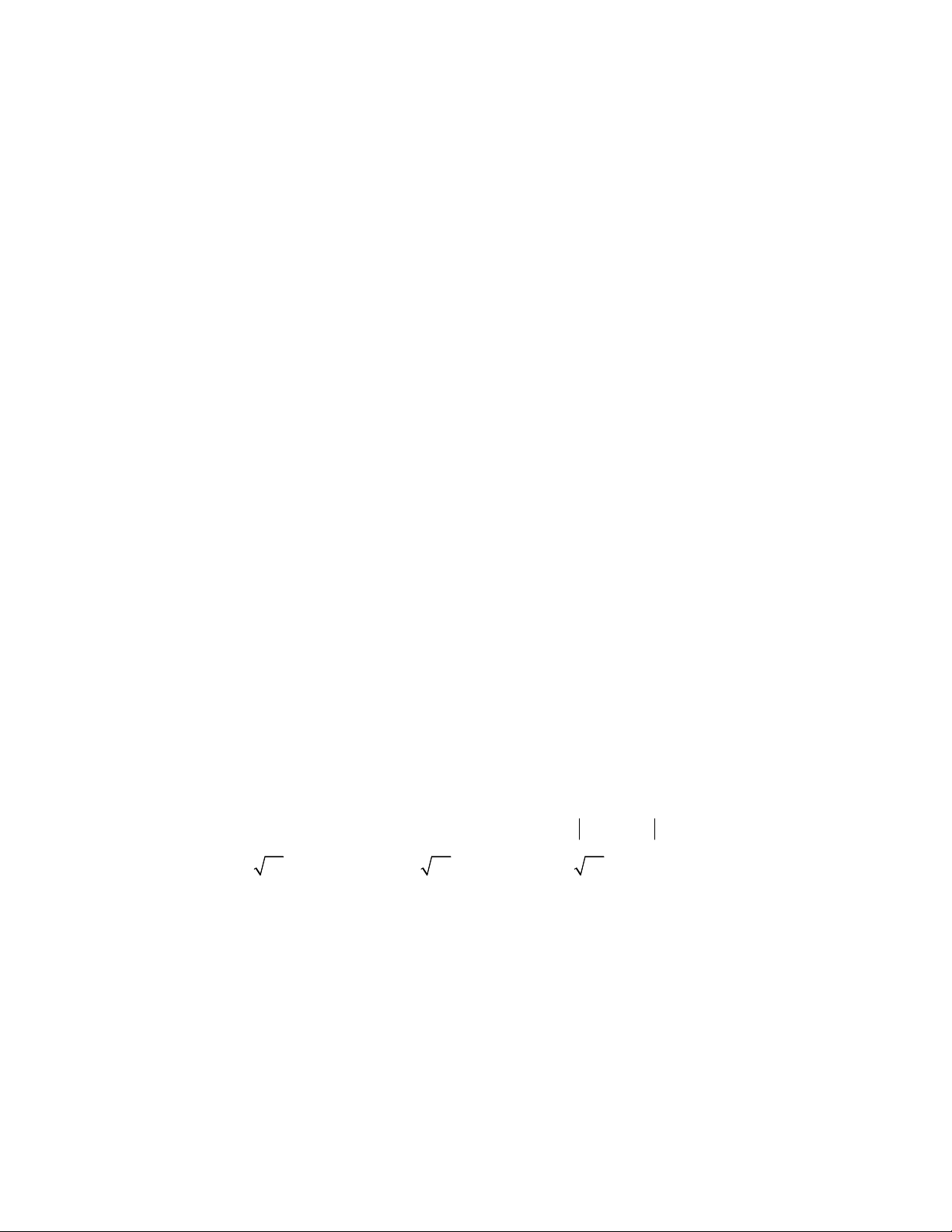
1
Phần I. ĐẶT VẤN ĐỀ
1. Lí do chọn đề tài
Tư duy có vai trò đặc biệt quan trọng đối với hoạt động thực tiễn cũng như đối
với hoạt động nhận thức của con người. Tư duy giúp con người nhận thức được quy
luật khách quan từ đó có thể dự kiến một cách khoa học xu hướng phát triển của sự
vật, hiện tượng và có kế hoạch biện pháp cải tạo hiện thực khách quan.
Có thể nói, khả năng tư duy là một trong những kỹ năng có giá trị nhất, có tính
ứng dụng cao nhất mà mỗi người cần có để học tập, làm việc có hiệu quả. Bởi ngày
này với sự phát triển của công nghệ và tri thức cao, người ta làm việc dựa trên kỹ
năng tư duy, mà không dung nhiều cơ bắp vào công việc. Mỗi người cần vận dụng
những tri thức, kỹ năng, kinh nghiệm của bản thân vào công việc của mình làm để
mang lại kết quả tốt hơn, có hiệu quả cao hơn.
Tư duy giúp con người thu thập, phân tích và sử dụng thông tin, ra quyết định
cũng như hợp tác với người khác để giải quyết vấn đề, đóng góp ý tưởng, phát triển
bản thân.
Tiềm năng của bộ não con người là rất lớn. Do đó, mỗi người hãy để cho não bộ
làm việc thường xuyên, luôn rèn luyện kỹ năng tư duy cho bản thân để học tập làm
việc có hiệu quả, đem đến năng suất cao.
Những người không có thói quen đặt câu hỏi, không có khả năng khám phá, lựa
chọn sẽ khó có thể tiến lên trong cuộc sống. Khả năng suy nghĩ, tư duy tốt sẽ giúp
cho những người trẻ, đặc biệt là các em học sinh phát triển bản thân, đạt được những
thành tích, thành công trong hiện tại và tương lai.
Trong những năm gần đây, đề thi tốt nghiệp trung học phổ thông Quốc gia (TN
THPT QG) luôn xuất hiện bài toán cực trị hình học trong không gian Oxyz. Chẳng
hạn: Câu 49, đề 104, đề thi TN THPT QG năm học 2020-2021: “Trong không gian
Oxyz
, cho hai điểm
2;1; 3 , 1; 3;2
A B
. Xét hai điểm
,
M N
thay đổi thuộc mặt
phẳng
Oxy
sao cho
3
MN
. Giá trị lớn nhất của
AM BN
bằng
A.
65
. B.
29
. C.
26
. D.
91
.
Trong quá trình dạy, nhận ra khi các em học sinh gặp bài chủ đề này đa số các
em, đặc biệt các em có học lực Khá, khá hoang mang, lo lắng, chưa biết định hướng
giải bài này như thế nào? Các em thường bỏ qua không làm mà cũng không phân
tích bài toán, đặt câu hỏi. Nguyên nhân một phần bởi thời gian chương trình, bài tập
về chủ đề này rất là ít và hạn chế, một phần bởi độ khó của bài tập, bài tập đưa ra
chưa hệ thống và chưa có giải pháp, định hướng, một phần bởi khả năng tư duy các
em học sinh.
Với những điều nhận ra, tôi mong muốn giúp các em rèn luyện tốt khả năng tư
duy, giúp các em có tâm lí tốt, biết cách đặt câu hỏi, phân tích khi gặp bài toán khó
để từ đó giải quyết được nó. Tôi mạnh dạn nghiên cứu đề tài: “Rèn luyện tư duy





















