
PHÒNG GIÁO D C VÀ ĐÀO T O DI N CHÂUỤ Ạ Ễ
TR NG TI U H C DI N NG C 2ƯỜ Ể Ọ Ễ Ọ
----------
SÁNG KI N KINH NGHI MẾ Ệ
T KI N TH C C B N V DI N TÍCH HÌNH TAM GIÁC PHÁTỪ Ế Ứ Ơ Ả Ề Ệ
TRI N, NÂNG CAO Đ B I D NG H C SINH NĂNG KHI U TOÁNỂ Ể Ồ ƯỠ Ọ Ế
Ng i th c hi n:ườ ự ệ Vò ThÞ
Minh
Đi n tho i: ệ ạ 01683949237
1

T KI N TH C C B N V DI N TÍCH HÌNH TAM GIÁC PHÁTỪ Ế Ứ Ơ Ả Ề Ệ
TRI N, NÂNG CAO Đ B I D NG H C SINH NĂNG KHI U TOÁNỂ Ể Ồ ƯỠ Ọ Ế
ĐT V N ĐẶ Ấ Ề
Đt n c ta trong th i k công nghi p hóa hi n đi hóa và h i nh pấ ướ ờ ỳ ệ ệ ạ ộ ậ
qu c t . Văn ki n h i ngh l n 4 Ban ch p hành TW Đng CSVN khóa VIIIố ế ệ ộ ị ầ ấ ả
(2/1993) kh ng đnh “Giáo d c là qu c sách hàng đu, là đng l c phát tri nẳ ị ụ ố ầ ộ ự ể
kinh t xã h i”. Th t v y, trong công cu c đi m i c a đt n c, c n cóế ộ ậ ậ ộ ổ ớ ủ ấ ướ ầ
nh ng con ng i có b n lĩnh, có năng l c ch đng dám nghĩ dám làm đữ ườ ả ự ủ ộ ể
thích ng v i đi s ng xã h i đang t ng ngày, t ng gi thay đi. Mu n v y,ứ ớ ờ ố ộ ừ ừ ờ ổ ố ậ
xã h i ph i d a vào giáo d c m i đáp ng đc đi u đó. Chính vì l đó,ộ ả ự ụ ớ ứ ượ ề ẽ
Đng đã nh n m nh m c tiêu giáo d c hi n nay là: “Nâng cao dân trí, đào t oả ấ ạ ụ ụ ệ ạ
nhân l c và b i d ng nhân tài”. Nh v y rõ ràng chúng ta ph i đi t ki nự ồ ưỡ ư ậ ả ừ ế
th c c b n v ng ch c đ nâng cao dân trí và đ đào t o nhân l c cho xã h i.ứ ơ ả ữ ắ ể ể ạ ự ộ
Trên n n t ng đó đ chúng ta b i d ng nhân tài. Chúng ta không th xâyề ả ể ồ ưỡ ể
d ng m t tòa lâu đài đ s trên m t n n móng không v ng vàng, l i càngự ộ ồ ộ ộ ề ữ ạ
không th đào t o nhân tài khi mà ki n th c c b n ch a v ng ch c. Chúng taể ạ ế ứ ơ ả ư ữ ắ
không th b i d ng h c sinh gi i theo ki u áp đt nh “c g p d ng thể ồ ưỡ ọ ỏ ể ặ ư ứ ặ ạ ế
này là làm th này” trong lúc h c sinh ch a hi u vì sao l i làm nh th . D yế ọ ư ể ạ ư ế ạ
nh v y vô hình chúng ta đã bi n h c sinh làm vi c nh m t cái máy r pư ậ ế ọ ệ ư ộ ậ
khuôn, thi u linh ho t trong làm bài và thi u sáng t o trong th c ti n. Chínhế ạ ế ạ ự ễ
vì v y, mu n b i d ng h c sinh gi i ph i đi t ki n th c c b n v ng ch cậ ố ồ ưỡ ọ ỏ ả ừ ế ứ ơ ả ữ ắ
t đó phát tri n, nâng cao d n đ các em chi m lĩnh ki n th c m t cách nhừ ể ầ ể ế ế ứ ộ ẹ
nhàng, th a mái và v ng ch c.ỏ ữ ắ
TH C TR NG C A V N ĐỰ Ạ Ủ Ấ Ề
Nh chúng ta đã bi t, ngay t khi b c chân vào tr ng ti u h c cácư ế ừ ướ ườ ể ọ
em đã đc làm quen v i hình tam giác d ng t ng th (phân bi t hình tamượ ớ ở ạ ổ ể ệ
giác trong s các hình khác: hình vuông, hình tròn ...). Lên đn l p 5, các emố ế ớ
m i h c các khái ni m c a hình tam giác nh đnh, góc, đáy, chi u cao t ngớ ọ ệ ủ ư ỉ ề ươ
ng v i các đáy và h c cách tính di n tích tam giác (tu n 17 – 18) và đcứ ớ ọ ệ ầ ượ
2
c ng c v cách tính di n tích c a nó thông qua n i dung ôn t p hình h củ ố ề ệ ủ ộ ậ ọ
cu i c p.ố ấ
Th c t qua nhi u năm d y h c cho th y, m c dù các em đã đc h cự ế ề ạ ọ ấ ặ ượ ọ
đy đ v cách xác đnh đáy và chi u cao t ng ng v i đáy nh :ầ ủ ề ị ề ươ ứ ớ ư
- Trong m t tam giác ta có th ch n b t kì m t c nh nào đó làm c nhộ ể ọ ấ ộ ạ ạ
đáy, t đnh đi di n v i c nh đáy k m t đng th ng vuông góc v i đáy taừ ỉ ố ệ ớ ạ ẻ ộ ườ ẳ ớ
đc đng cao c a tam giácượ ườ ủ
- Cách k đng cao: Đt m t c nh góc vuông c a eke trùng v i đnhẻ ườ ặ ộ ạ ủ ớ ỉ
c a tam giác, c nh góc vuông kia trùng c nh đi di n v i đnh đ v .ủ ạ ạ ố ệ ớ ỉ ể ẽ
Th nh ng khi v n d ng vào làm m t s bài t p các em không kh iế ư ậ ụ ộ ố ậ ỏ
lúng túng nh t là tr ng h p đng cao n m ngoài tam giác.ấ ườ ợ ườ ằ
Còn cách tính di n tích hình tam giác đã đc sách giáo khoa gi i thi uệ ượ ớ ệ
cách tính di n tích khi đã bi t đáy và chi u cao c a nó. Nh ng trong th c t taệ ế ề ủ ư ự ế
có th tính di n tích hình tam giác b ng cách so sánh di n tính. Do đó áp d ngể ệ ằ ệ ụ
đ làm m t s bài t p c th , h c sinh v n không tránh kh i nh ng khó khăn,ể ộ ố ậ ụ ể ọ ẫ ỏ ữ
lúng túng đc bi t là tr ng h p tính di n tích hình tam giác khi mà ta ch aặ ệ ườ ợ ệ ư
bi t c th đ dài đáy và chi u cao c a nó.ế ụ ể ộ ề ủ
C th , sau khi h c xong ph n di n tích hình tam giác các em áp d ngụ ể ọ ầ ệ ụ
làm m t s bài t p đn gi n nh sách giáo khoa, tôi đã cho h c sinh l p b iộ ố ậ ơ ả ư ọ ớ ồ
d ng kh o sát qua m t s bài t p nh (trong th i gian 40 phút) nh sau:ưỡ ả ộ ố ậ ỏ ờ ư
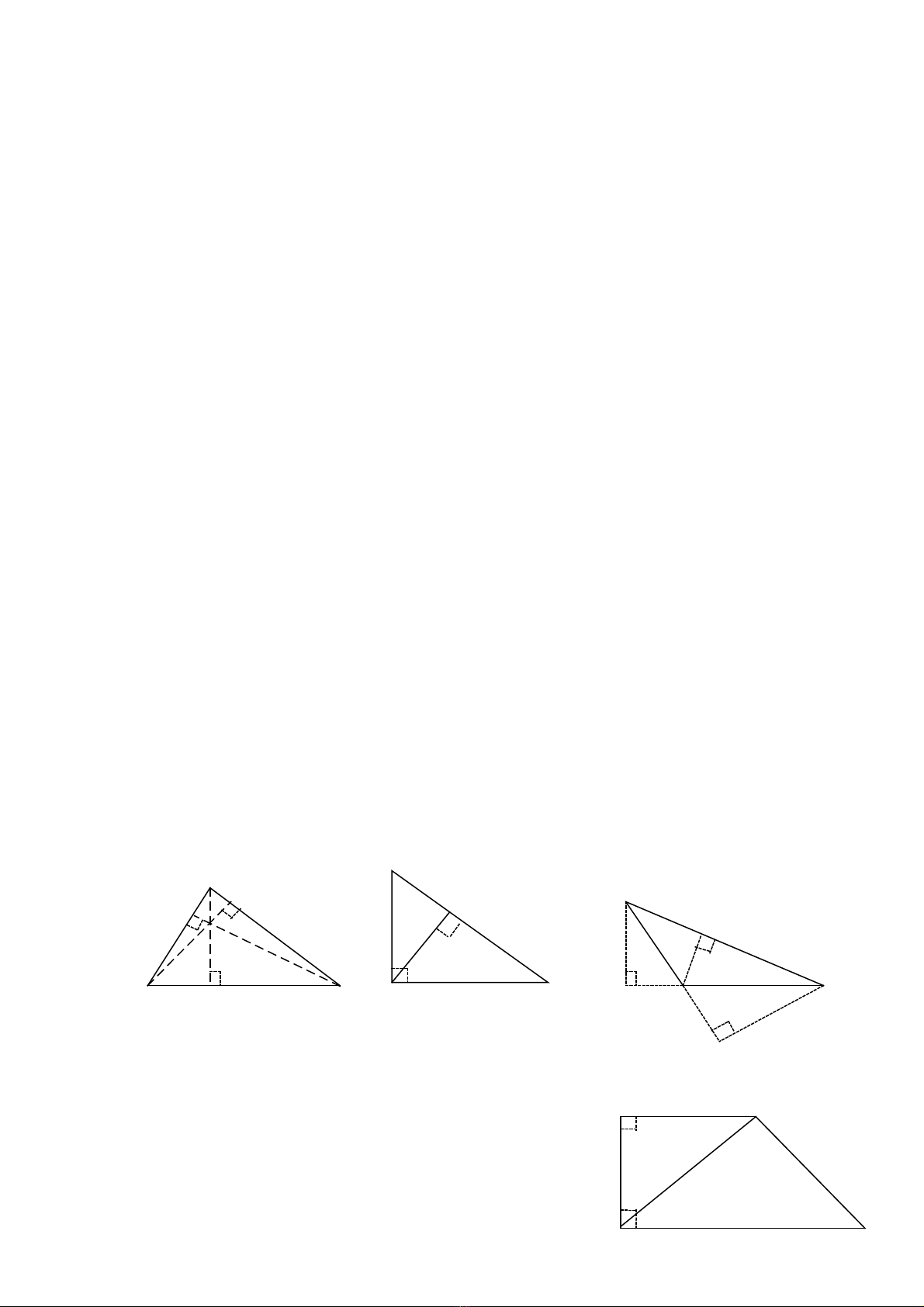
Bài 1: (30. đi m): Nêu tên c nh đáy và đng cao t ng ng trong m iể ạ ườ ươ ứ ỗ
hình tam giác.
Bài 2: (2.0 đi m): Cho hình thang vuôngể
ABCD (xem hình v ) có AB = 12cm, DC = 15cm,ẽ
AD = 13cm. N i D v i B đc hai tam giác ABDố ớ ượ
và BDC.
3
A
B CH
KI
D
E G
SM
T
P
Q
N
L
Hình 1 Hình 2 Hình 3
A B
D C
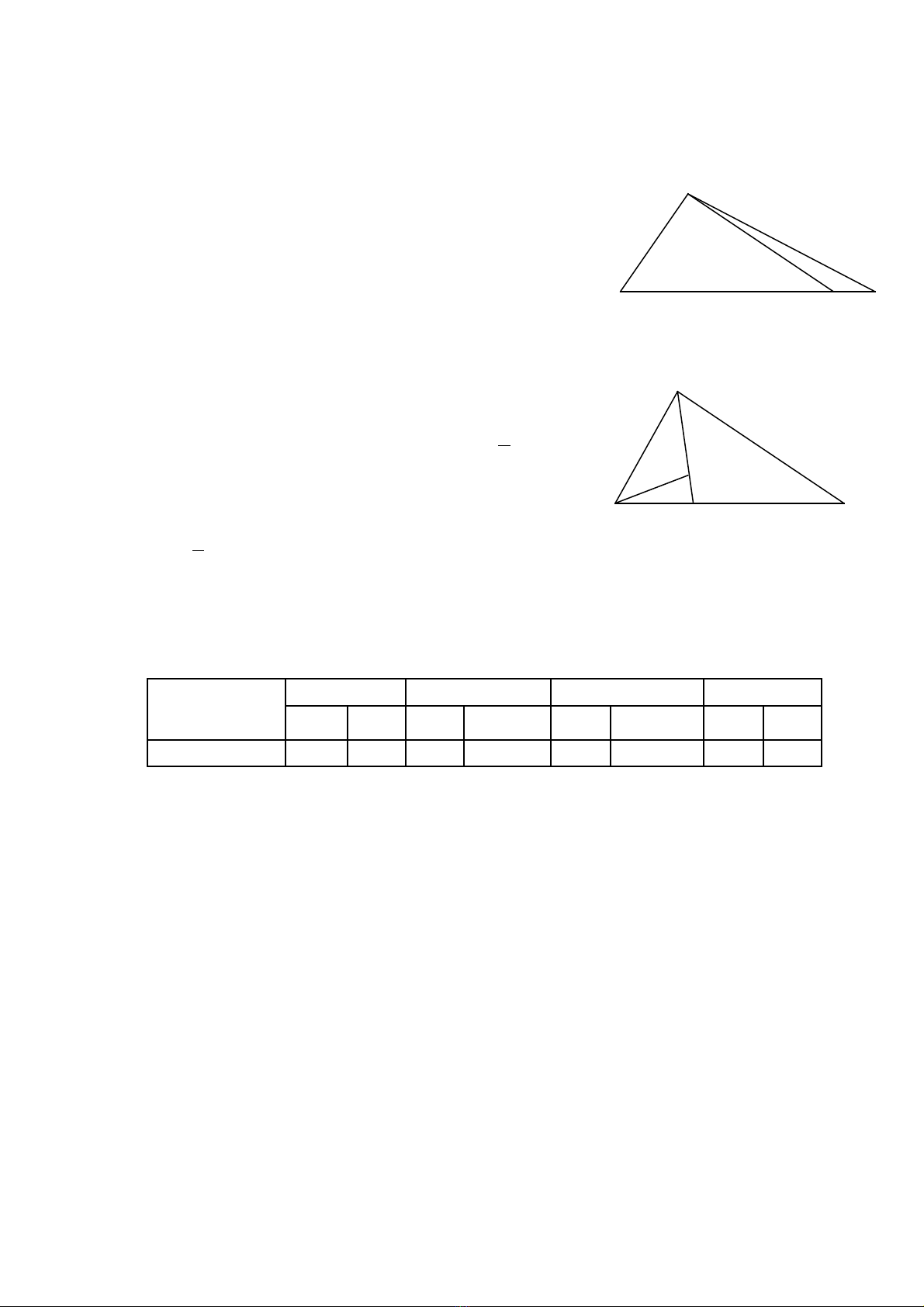
a) Tính di n tích m i tam giác đó?ệ ỗ
b) Tính t s ph n trăm c a di n tích hình tam giácỉ ố ầ ủ ệ
ABD và di n tích hình tam giác BDC.ệ
Bài 3 (2,5 đi m): Cho hình tam giác ABC cóể
di n tích 24cmệ2. N u kéo dài đáy BC thêm m tế ộ
đo n dài 2cm thì di n tích tăng thêm là bao nhiêu?ạ ệ
Bi t đáy hình tam giác ban đu là 8cmế ầ
Bài 4 (2,5 đi m): Cho tam giác ABC. Trênể
c nh đáy BC l y đi m D sao cho ạ ấ ể
.DC
2
1
BD
N iố
A v i D. Trên c nh AD l y đi m M sao choớ ạ ấ ể
.AD
3
1
DM
Tính di n tích tam giá ABC bi t di n tích tam giácệ ế ệ
BMD = 4cm2.
Sau 40 phút làm bài, k t qu thu đc t h c sinh nh sau:ế ả ượ ừ ọ ư
S h c sinhố ọ
kh o sátả
Y uếTB KháGi iỏ
SL TL SL TL SL TL SL TL
30 0 0% 13 43,34% 17 56,66% 0 0%
Qua ch m bài kh o sát, k t qu cho th y:ấ ả ế ả ấ
* bài 1: Hình 1 và hình 2 c 30 em đu tìm đúng và đ các c nh vàỞ ả ề ủ ạ
đng cao t ng ng v i c nh đy. Nh ng sang hình 3 ph n l n các em chườ ươ ứ ớ ạ ấ ư ầ ớ ỉ
tìm đc c nh đáy MP và đng cao t ng ng v i nó NT còn đng caoượ ạ ườ ươ ứ ớ ườ
ML t ng ng v i c nh đáy PN và đng cao PQ t ng ng v i đáy MN thìươ ứ ớ ạ ươ ươ ứ ớ
r t ít em làm đc.ấ ượ
* bài 2 c 30 em đu làm theo đúng đáp s chi m t l 100%.Ở ả ề ố ế ỷ ệ
Tuy nhiên c 30 em đu làm theo m t cách đó là áp d ng công th c đả ề ộ ụ ứ ể
thay s và tính, không em nào bi t cách dùng t s hai đáy đ tính nh :ố ế ỉ ố ể ư
Dienj tích tam giác ABD là: 12 x 13 : 2 = 78 ( cm2)
Di n tích tam giác ABD và BDC có chi u cao b ng nhau (b ng chi uệ ề ằ ằ ề
cao hình thang)
4
A
BC D
2c
m
8c
m
24cm2
A
C
D
M
B

T s hai đáy AB và DC là: 12:15 = ỷ ố
5
4
V y t s di n tích c a hai tam giác ABD và BDC là ậ ỷ ố ệ ủ
5
4
Di n tích tam giác BDC là 78: ệ
5
4
= 97,5 (cm2)
T s ph n trăm c a di n tích hình tam giác ABD và di n tích tam giácỉ ố ầ ủ ệ ệ
BDC là: 4:5 = 0,8
0,8 = 80%
* bài t p 3, ph n l n các em tìm ra đáp s nh ng nhi u em lý lu nỞ ậ ầ ớ ố ư ề ậ
ch a ch t ch . Cũng nh bài 1 các em ch a bi t tìm di n tích ph n mư ặ ẽ ư ở ư ế ệ ầ ở
r ng b ng cách d a vào t s đ dài hai đáy.ộ ằ ự ỉ ố ộ
* Sang bài t p 4 đa s các em v hình đúng, đp và chính xác nh ngậ ố ẽ ẹ ư
không có em nào tính đc di n tích tam giác ABC b i vì đ gi i đc bàiượ ệ ở ể ả ượ
này thì đòi h i các em ph i n m v ng m i quan h gi a các y u t trong m tỏ ả ắ ữ ố ệ ữ ế ố ộ
tam giác đáy (đáy, chi u cao t ng ng v i đáy và di n tích).ề ươ ứ ớ ệ
Ta th y trong th c ti n d y toán, không ph i bài toán nào cũng d ngấ ự ễ ạ ả ở ạ
t ng minh nh bài t p 2 và 3 ch c n d a vào công th c là tính ngay đcườ ư ậ ỉ ầ ự ứ ượ
k t qu . Đc bi t là trong quá trình d y b i d ng h c sinh năng khi u, đế ả ặ ệ ạ ồ ưỡ ọ ế ể
đáp ng đc nhu c u h c t p c a h c sinh, giáo viên ph i s u t m, thi t kứ ượ ầ ọ ậ ủ ọ ả ư ầ ế ế
nh ng bài toán nâng cao h n, khái quát h n th ng nh ng bài toán đcữ ơ ơ ườ ữ ượ
“ng y trang “ b i nh ng đi u ki n ch a t ng minh. B i v y s không tránhụ ở ữ ề ệ ư ườ ở ậ ẽ
kh i nh ng v ng m c, khó khăn n u giáo viên không có ph ng pháp giúpỏ ữ ướ ắ ế ươ
h c sinh n m v ng m i quan h gi a các y u t trong m t tam giác.ọ ắ ữ ố ệ ữ ế ố ộ
Trong quá trình nghiên c u và qua th c t gi ng d y nhi u năm, đcứ ự ế ả ạ ề ặ
bi t là qua hai năm th c hi n ch ng trình thay sách l p 5 tôi th y khó khănệ ự ệ ươ ớ ấ
nh t khi d y các toán v tam giác v n là nh ng tr ng h p sau đây.ấ ạ ề ẫ ữ ườ ợ
- Tr ng h p 1ườ ợ : V đng th ng đ chia tam giác đã cho thành cácẽ ườ ẳ ể
ph n theo m t t l di n tích nào đó.ầ ộ ỉ ệ ệ
+ Ví d 1: Cho tam giác ABC, qua đnh A v m t đng th ng c tụ ỉ ẽ ộ ườ ẳ ắ
c nh BC t i đi m D sao cho di n tích tam gi c ABD b ng ạ ạ ể ệ ấ ằ
5
1
di n tích tamệ
giác ADC.
5


























