
M C L CỤ Ụ
N i dungộTrang
A. M đuở ầ 1
I. Lí do ch n đ tàiọ ề 1
II. M c đích nghiên c uụ ứ 1
III. Đi t ng nghiên c uố ượ ứ 1
IV. Ph ng pháp nghiên c uươ ứ 1
B. N i dung SKKNộ2
I) KI N TH C C B NẾ Ứ Ơ Ả Đ GI I QUY T D NG TOÁN Ể Ả Ế Ạ
NÀY
2
II) CÁC BÀI TOÁN ĐI N HÌNH S D NG PH NG PHÁPỂ Ử Ụ ƯƠ 3
1. Hàm đc tr ng có d ng hàm s đa th c b c 2, b c 3, b c 4ặ ư ạ ố ứ ậ ậ ậ 3
2. Hàm đc tr ng có d ng hàm s ch a căn th cặ ư ạ ố ứ ứ 10
3. S d ng ph ng pháp th , c ng đi s sau đó k t h p v iử ụ ươ ế ộ ạ ố ế ợ ớ
ph ng phápươ hàm số
15
IV. Hi u qu do sáng ki n đem l iệ ả ế ạ 18
V. Đ xu t, ki n nghề ấ ế ị 18
Danh m c các tài li u tham kh oụ ệ ả 20
A. M ĐUỞ Ầ
I. LÍ DO CH N Đ TÀI Ọ Ề
1

Trong nh ng năm g n đây, các đ thi đi h c và h c sinh gi i luônữ ầ ề ạ ọ ọ ỏ
xu t hi n bài toán gi i h v i đ khó ngày càng tăng. M t trong nh ng lo iấ ệ ả ệ ớ ộ ộ ữ ạ
h hay g p trong các k thi và gây cho h c sinh khó khăn khi ti p c n là lo iệ ặ ỳ ọ ế ậ ạ
h trong đó có s d ng ph ng pháp hàm s .ệ ử ụ ươ ố
Do v y, vi c c n tìm ra m t con đng ng n nh t, l a ch n hàm s thíchậ ệ ầ ộ ườ ắ ấ ự ọ ố
h p, th c hi n các thao tác đn gi n, ti t ki m t i đa th i gian đ gi i toán làợ ự ệ ơ ả ế ệ ố ờ ể ả
m t v n đ tôi luôn trăn tr .ộ ấ ề ở
Trong bài vi t này tôi mu n trình bày m t s kinh nghi m t duy ápế ố ộ ố ệ ư
d ng đ tìm con đng khai thông nh m gi i quy t bài toán m t cách g nụ ể ườ ằ ả ế ộ ọ
gàng. B ng vi c s d ng m t s bài toán m c đ thi đi h c và thi h c sinhằ ệ ử ụ ộ ố ở ứ ộ ạ ọ ọ
gi i làm ví d minh h a, tôi đi sâu vào vi c phân tích các kh năng ti p c nỏ ụ ọ ệ ả ế ậ
l i gi i, d n ra nh ng cách gi i t ng ng, đa ra nh ng phân tích, nh n xétờ ả ẫ ữ ả ươ ứ ư ữ ậ
phù h p, đ t đó h c sinh có th n m b t đc ý t ng, con đng t duyợ ể ừ ọ ể ắ ắ ượ ưở ườ ư
mà m i ng i làm toán c n rèn luy n khi đng tr c m t bài toán gi i h .ỗ ườ ầ ệ ứ ướ ộ ả ệ
II) M C ĐÍCH NGHIÊN C UỤ Ứ
-Rèn luy n kĩ năng s d ng ph ng pháp hàm s đ gi i h .ệ ử ụ ươ ố ể ả ệ
- Rèn luy n t duy logic, kh năng nhìn nh n, đánh giá chung nh m tìmệ ư ả ậ ằ
ra con đng h p lí đ có đnh h ng nh m đa ra gi i pháp t t nh tườ ợ ể ị ướ ằ ư ả ố ấ
khi g p m t bài toán c th .ặ ộ ụ ể
- Rèn luy n các kĩ năng t ng h p v t duy và kĩ x o toán h c.ệ ổ ợ ề ư ả ọ
III) ĐI T NG NGHIÊN C U:Ố ƯỢ Ứ
-Các bài toán gi i h có th s d ng ph ng pháp hàm s đ gi iả ệ ể ử ụ ươ ố ể ả
quy tế
-Các d ng toán v h trong các kì thi HSG và Đi h c trong nh ng nămạ ề ệ ạ ọ ữ
g n đây.ầ
IV) PH NG PHÁP NGHIÊN C U:ƯƠ Ứ
2

-Nghiên c u xây d ng c s lí thuy t gi i bài toán h b ng ph ngứ ự ơ ở ế ả ệ ằ ươ
pháp hàm s ố
- Nghiên c u kh năng áp d ng trên c s th c ti n ti p thu c a các điứ ả ụ ơ ở ự ễ ế ủ ố
t ng h c sinh đã và đang đc truy n th .ượ ọ ượ ề ụ
B. N I DUNG SÁNG KI N KINH NGHI MỘ Ế Ệ
I) KI N TH C C B NẾ Ứ Ơ Ả Đ GI I QUY T D NG TOÁN NÀYỂ Ả Ế Ạ
Tính ch t 1: ấGi s hàm s ả ử ố
( )
y f x=
đng bi n (ngh ch bi n) trênồ ế ị ế
mi n D và ề
;u v D
, khi đó
( ) ( )
.f u f v u v= =�
Tính ch t 2: ấN u hàm s ế ố
( )
y f x=
đng bi nồ ế trên D và
( )
y g x=
là
hàm h ngằ ho c là m t hàm s ặ ộ ố ngh ch bi nị ế trên D thì ph ng trìnhươ
( ) ( )
f x g x=
có nhi u nh t m t nghi m thu c kho ng D.ề ấ ộ ệ ộ ả
Khi g p h có d ng ặ ệ ạ
( ) ( ) ( )
( ) ( )
1
; 0 2
f x f y
g x y
=
=
Xét hàm s ố
( )
y f t=
, ta th ng g p tr ng h p hàm s liên t c trong t p xácườ ặ ườ ợ ố ụ ậ
đnh c a nó.ị ủ
N u hàm s ế ố
( )
y f t=
đn đi u, thì t (1) suy ra ơ ệ ừ
x y=
. Khi đó bài toán
đa v gi i ph ng trình (2) theo n ư ề ả ươ ẩ x (ho c ặy).
N u hàm s ế ố
( )
y f t=
có m t c c tr t i ộ ự ị ạ
t a=
thì nó thay đi chi u bi nổ ề ế
thiên m t l n khi qua ộ ầ a. T (1) suy ra ừ
x y=
ho c ặ
,x y
n m v hai phía c a ằ ề ủ a.
Vân dung linh hoat cac đinh li, tính ch t trên, t môt ph ng trinh ân ' ' ' ' ấ ư ' ươ (
,x
ta se đa hai vê vê dang ư '
( ) ( )
f h x f g x=� � � �
� � � �
II) CÁC BÀI TOÁN ĐI N HÌNH S D NG PH NG PHÁPỂ Ử Ụ ƯƠ
1. Hàm đc tr ng có d ng hàm s đa th c b c 2, b c 3, b c 4ặ ư ạ ố ứ ậ ậ ậ
Bài 1.Gi i h : ả ệ
( )
( ) ( )
( )
2
2 2
4 1 3 5 2 0 1
4 2 3 4 7 2
x x y y
x y x
+ + − − =
+ + − =
3

Phân tích: Ta nh n th y khó có th b t đu v i ph ng trình ậ ấ ể ắ ầ ớ ươ (2), đ ý đnể ế
ph ng trình ươ (1),
2
4 1x+
là bi u th c b c hai c a ể ứ ậ ủ
x
và
3y−
có th coi làể
bi u th c b c hai c a ể ứ ậ ủ
5 2y−
. N u đt ế ặ
5 2t y= −
thì
( )
( )
2
2
5 1
3 5 2 3 1
2 2
t
y y t t t
� �
− −
− − = − = +
� �
� �
Bi u th c ể ứ
( )
2
1t t+
có hình th c gi ng v i ứ ố ớ
( )
2
4 1 2x x+
, do v y ta s bi n điậ ẽ ế ổ
( )
1
v d ng ề ạ
( ) ( )
f u f v=
. Đ đa v d ng này ta th ng “cô l p” bi n, doể ư ề ạ ườ ậ ế
v y s chuy n ậ ẽ ể
( )
3 5 2y y− −
sang v ph i c a ế ả ủ
( )
1
.
Gi i: ảĐi u ki n ề ệ
3 5
;
4 2
x y
. Khi đó
( )
( )
( )
2
1 4 1 .2 5 2 1 5 2x x y y+ = − + −�
(3)
Xét hàm s ố
( )
( )
2 3
1 ,f t t t t t= + = +
v i ớ
t
ᄀ
Ta có
( )
2
' 3 1 0, tf t t= + > ∀ ᄀ
nên
( )
f t
đng bi n trên ồ ế
ᄀ
(3)
2 5 2x y= −
Thay
2
5 4
2
x
y−
=
vào (2) ta đc:ượ
2
2 2
5
4 2 2 3 4 7 0
2
x x x
� �
+ − + − − =
� �
� �
(4)
Phân tích: Ph ng trình ươ (4) trông khá “ph c t p” nên ta đnh h ngứ ạ ị ướ
s d ng ph ng pháp hàm s đ gi i quy tử ụ ươ ố ể ả ế
Nh n th y ậ ấ
0x
=
và
3
4
x=
không là nghi m c a ph ng trình (4)ệ ủ ươ
Xét hàm s ố
( )
2
2 2
5
4 2 2 3 4 7
2
g x x x x
� �
= + − + − −
� �
� �
v i ớ
3
0; 4
x� �
� �
� �
, ta có:
( )
( )
2 2
5 4 4 3
' 8 8 2 4 4 3 0, 0;
2 4
3 4 3 4
g x x x x x x x
x x
� � � �
= − − − = − − < ∀
� � � �
− −
� � � �
4
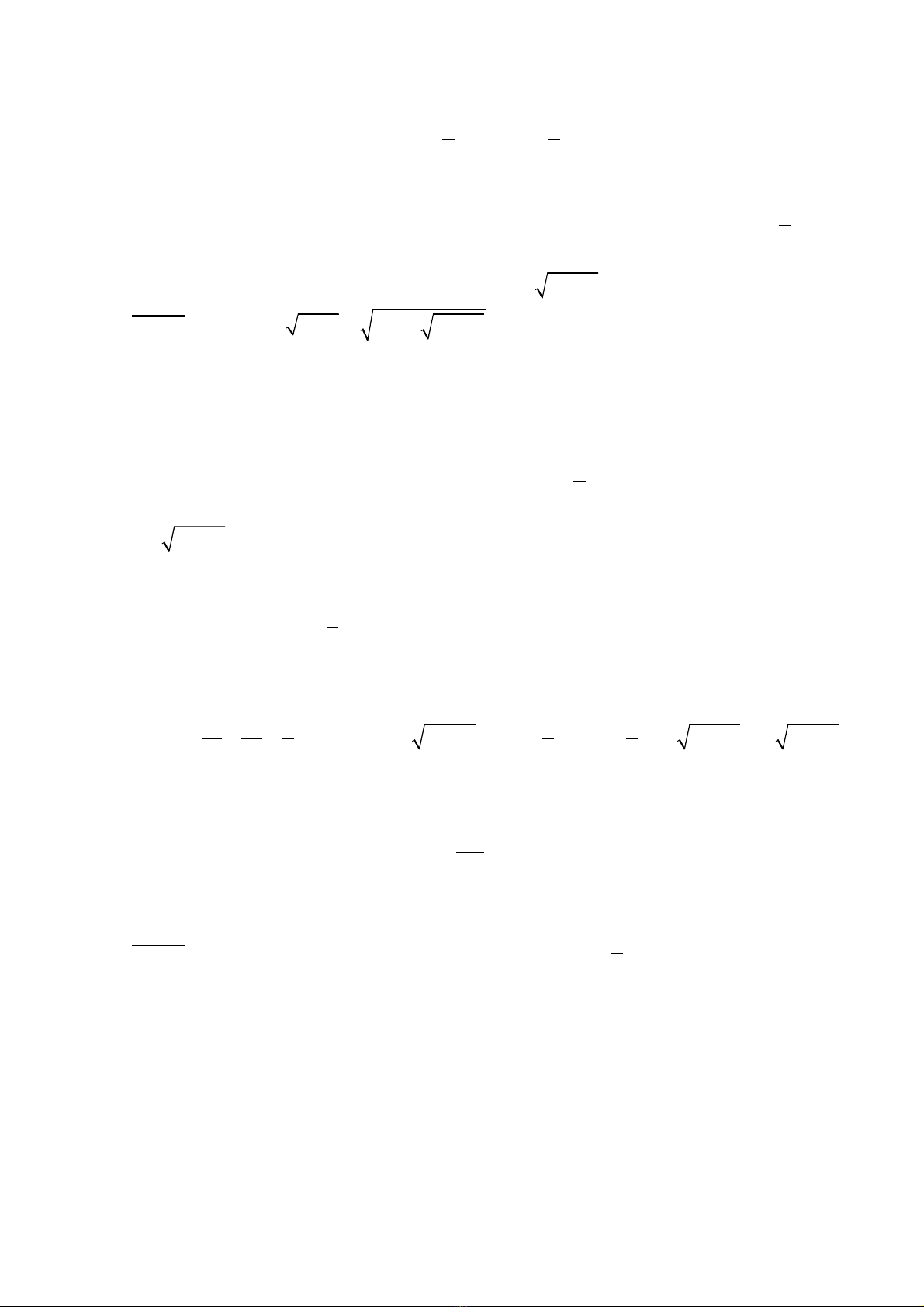
Do đó
( )
g x
ngh ch bi n trên ị ế
3
0; 4
� �
� �
� �
. Mà
10
2
g� �
=
� �
� �
nên ph ng trình (4) cóươ
nghi m duy nh t ệ ấ
1
2
x=
suy ra
2y=
. V y h đã cho có nghi m ậ ệ ệ
( )
1
; ;2
2
x y � �
=� �
� �
.
Bài 2. Gi i h ả ệ
( ) ( )
( )
3 2 3
3
2 4 3 1 2 2 3 2 1
2 14 3 2 1 2
x x x x y y
x x y
− + − = − −
+ = − − +
Phân tích: Ta không th b t đu v i ph ng trình ể ắ ầ ớ ươ (2) vì khó có s bi nự ế
đi nào h p lý đây. Xét ph ng trình ổ ợ ở ươ (1), th c hi n cô l p bi n b ng, chiaự ệ ậ ế ằ
hai v cho ế
3
x
ta th y v trái là b c ba đi v i ấ ế ậ ố ớ
1
x
, v ph i là b c ba đi v iế ả ậ ố ớ
3 2t y= −
, do v y ta có th bi n đi đa v d ng ậ ể ế ổ ư ề ạ
( ) ( )
f u f v=
.
HD: Đi u ki n: ề ệ
2
3
2
x
y
−
Xét th y ấx = 0 không th a mãn h , nên chia hai v ỏ ệ ế
c a ph ng trình (1) cho ủ ươ
3
x
ta đc: ượ
( ) ( )
( )
( )
33
3 2
1 3 4 1 1
1 2 4 2 3 2 1 1 3 2 3 2 3y y y y
x x x x x
� � � �
− + − + = − − − + − = − + −� � � � � �
� � � �
Xét hàm s ố
( )
3
,f t t t t= + ᄀ
. Ta có
( )
2
' 3 1 0f t t t= + > ∀ ᄀ
nên hàm s ố
( )
f t
H có nghi m duy nh t ệ ệ ấ
111
798
x y= =�
.
Bài 3. (Kh i A năm 2012ố) Gi i h : ả ệ
3 2 3 2
2 2
3 9 22 3 9
1
2
x x x y y y
x y x y
− − + = + −
+ − + =
Phân tích: Hai v c a ph ng trình đu đu có d ng b c 3 (v i haiế ủ ươ ầ ề ạ ậ ớ
bi n x, y), nên ta đnh h ng đa ph ng trình đu v d ng ế ị ướ ư ươ ầ ề ạ
( ) ( )
f u f v=
, tuy
nhiên hàm đc tr ng lúc đó ặ ư
( )
3
12f t t t= −
không đn đi u trên ơ ệ
ᄀ
do đó ta
5





















