Bài 4
PHÂN TÍCH CHUỖI THỜI GIAN
Khái niệm
Trong thực tế để mô hình hoá một hiện tượng kinh tế người ta có thể sử dụng
hai loại mô hình:
- Mô hình cấu trúc: Biểu diễn sự thay đổi của một biến kinh tế trong mối
liên hệ phụ thuộc với các biến khác.
- Mô hình hành vi: Biểu diễn sự thay đổi của một biến chỉ dựa vào hành vi
của quá khứ của chính bíên đó.
Mô hình cấu trúc chỉ được sử dụng hiệu quả khi biết rõ những nhân tố ảnh
hưởng đến sự biến động của biến cần phân tích, mặt khác để dự báo lại phải dự
báo được bản thân các nhân tố ảnh hưởng đó. Điều đó đôi khi còn khó khăn hơn
dự báo bản thân biến cần phân tích.
Ngoài ra trong nhiều trường hợp sự biến động của biến cần phân tích không
thể giải thích được thông qua các nhân tố khác. Điều đó có thể do ta không biết rõ
các nhân tố ảnh hưởng nên nếu dùng mô hình cấu trúc thì hoặc các hệ số góc đều
không có ý nghĩa thống kê hoặc không có ích cho dự báo. Mặt khác cũng có thể do
sự biến động của biến cần phân tích chỉ phụ thuộc vào sự vận động của bản thân
nó. Lúc đó dùng mô hình hành vi hiệu quả hơn.
Phân tích chuỗi thời gian nghiên cứu hành vi, khuôn mẫu trong quá khứ của
một biến và sử dụng những thông tin này để dự đoán những thay đổi trong tương
lai.
1. Định nghĩa
Chuỗi thời gian là tập hợp các giá trị của một biến ngẫu nhiên được sắp xếp
theo thứ tự thời gian.
Chuỗi thời gian còn được gọi là dãy số thời gian. Đơn vị thời gian có thể là
ngày, tuần, tháng, quí, năm. . .Chuỗi thời gian được ký hiệu là Xt, Yt, Zt. . .
Phân tích chuỗi thời gian có mục đích là làm rõ cấu trúc của chuỗi thời gian
(tức là các thành phần của nó) trong sự biến động của bản thân nó. Trên cơ sở đó
có thể thấy rõ hơn bản chất cũng như quy luật của hiện tượng thông qua một chỉ
tiêu cụ thể, từ đó có thể dự báo ngắn hạn giá trị của chuỗi đó.
2. Các thành phần của chuỗi thời gian
Có thể nói bất kỳ chuỗi thời gian nào cũng chứa đựng ít nhất một trong bốn
thành phần (yếu tố) sau:
- Xu thế biến động;
- Biến động theo mùa (hoặc thời vụ);
- Biến động theo chu kỳ;
- Biến động ngẫu nhiên (bất quy tắc);
Tức là có thể nói rằng cấu trúc của chuỗi thời gian sẽ bao gồm 4 thành phần
nói trên. Ký hiệu:
Tt (Trend)- thành phần xu thế cho biết xu hướng biến động của chuỗi thời
gian trong một khoảng thời gian tương đối dài.
Đa số chuỗi thời gian thể hiện một khuynh hướng tăng hoặc giảm khá rõ theo
thời gian. VD: GDP, GNP, thu nhập theo đầu người. . .
St (season) - thành phần mùa vụ cho ta biết sự biến động của chuỗi trong
hai hay nhiều khoảng thời gian (độ dài có thể khác nhau) liền nhau được lập đi lập
lại trong suốt thời kỳ xem xét.
Các biến động mùa vụ có thể diễn ra theo quý (GDP), theo tháng, thậm chí
trong từng ngày.
Ct (cycle) - thành phần chu kỳ cho biết mức độ biến động của chuỗi trong
một khoản thời gian nào đó (gọi là chu kỳ) sẽ được lặp đi lặp lại trong suốt thời kỳ
nghiên cứu. Thành phần chu kỳ này không liên quan đến yếu tố mùa vụ mà bắt
nguồn từ chu kỳ kinh doanh cũng như chu kỳ kinh tế.
It (Irregular) - thành phần bất quy tắc là kết hợp của vô số các nhân tố ảnh
hưởng đến hành vi của chuỗi, tương tự như các nhân tố hình thành nên các sai số
ngẫu nhiên ui trong mô hình hồi qui.
Về mặt cấu trúc có hai loại mô hình chuỗi thời gian sau đây:
*Mô hình cộng: là mô hình mà các giá trị thực của chuỗi thời gian được viết dưới
dạng:
Yt = Tt + St + Ct + It
Mô hình này ít được dùng trong thực tế vì nó không cho phép phân tích sự ảnh
hưởng qua lại giữa các thành phần tạo nên chuỗi. Mô hình cộng thường chỉ sử
dụng khi biết rằng chuỗi thời gian chỉ bao gồm hai trong ba thành phần (Tt, St, Ct
) và It đồng thời các thành phần đó lại tác động độc lập với nhau lên sự biến động
của Yt.
*Mô hình nhân: là mô hình mà các giá trị thực của chuỗi thời gian được mô tả
dưới dạng:
Yt = Tt*St*Ct*It
Đây là mô hình thường được sử dụng nhất, trong đó Tt được biểu diễn bằng
giá trị cùng đơn vị đo với Yt, các thành phần còn lại được đo bằng %. Ví dụ: Tto=
35 triệu, Sto = 1.55; Cto=0.92; Ito = 0.8. Lúc đó ta có:
Yto = 35*1.55*0.92*0.8 = 39.928 triệu
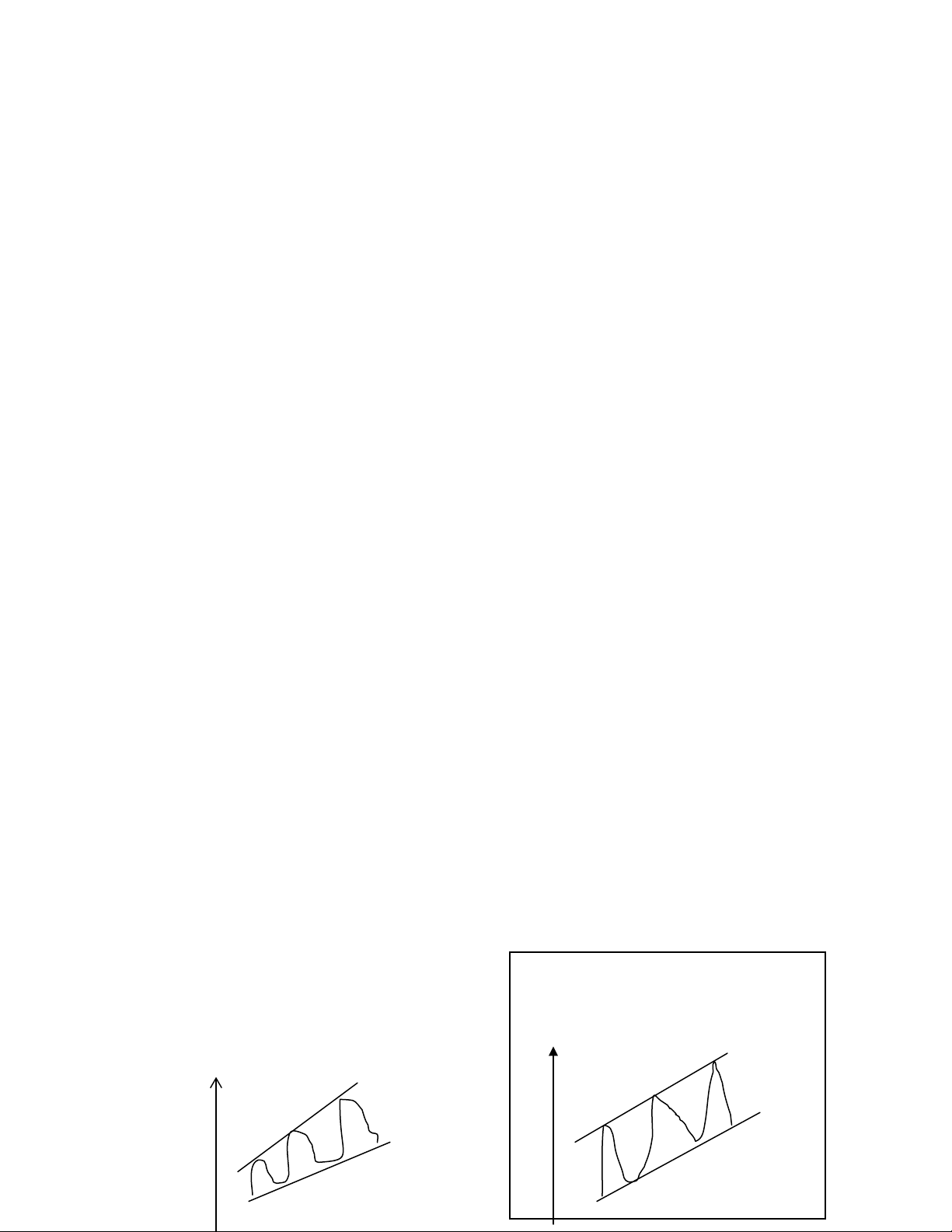
Một trong các phương pháp để nhận biết nên dùng phương pháp nào là qua
quan sát đồ thị:
Y
t
Yt
t
Mô hình nhân Mô hình cộng
3. Phân tích xu thế
3.1. Các mô hình ngoại suy giản đơn.
Đa phần các chuỗi thời gian là các chuỗi không liên tục, bao gồm các quan sát
rời rạc trong một khoảng thời gian nào đó. Ta ký hiệu chuỗi này là Yt với t = 1,2,. .
.,n. Tìm được xu thế của Yt trong quá khứ sẽ cho phép ta dự báo giá trị cuả Yt
trong tương lai. Ta sẽ ký hiệu các giá trị dự báo là Y, t = n+1, n+2, . . .
∧
t
Giả sử với t = 1,2, . . .,n ta biểu diễn Yt là một hàm liên tục của t.