Kiểm định t và hoán chuyển số liệu trong lâm sàng thống kê: Bài 5

Chng trình hun luyn y khoa – YKHOA.NET Training – Nguyn Vn Tun 1

Lâm sàng thng kê

Kim nh t và hoán chuyn s liu

Hi: “Tôi nghe nói rng khi ánh giá s khác bit gia hai nhóm bng t-test cn

phi chuyn i s liu. Ti sao?”

 ánh giá  khác bit gia hai nhóm, chúng ta thưng s dng phương pháp

kim nh t (hay t-test). Kim nh t có l là mt trong nhng phương pháp ơn gin

nht trong thng kê hc, vì có th tính toán mt cách th công, mà không cn n máy

tính hay phn mm phân tích s liu (nhưng nu có thì tt hơn!)

Tuy ơn gin, nhưng phương pháp kim nh t cng rt d sai lm. Sai lm thông

thưng nht là không  ý n nhng gi nh ng sau phương pháp này. Phương pháp

kim nh t ch thích hp nu s liu áp ng nhng iu kin hay gi nh sau ây:

• Hai nhóm so sánh phi hoàn toàn c lp nhau;

• Bin so sánh phi tuân theo lut phân phi chun (Gaussian distribution);

• Phương sai ca hai nhóm bng nhau, hay gn bng nhau; và

• Các i tưng phi ưc chn mt cách ngu nhiên (random sample).

Th nào là “c lp”? Khi nói n c lp ây là nói n hai nhóm không có

tương quan nhau. Ch!ng h"n như mt nhóm 1 g#m bnh nhân A, B, C và D; nhóm 2

g#m bnh nhân E, F, G và H, thì hai nhóm này c lp nhau. Nhưng nu có mt nhóm

bnh nhân mà o hai ln, thì hai bin s ca hai ln o ó không c lp v$i nhau. c

lp cng có ngh%a là không liên h nhau. Ch!ng h"n như nu 2 bnh nhân trong nhóm 1

(A và C) có liên h huyt thng, và nu bin mà chúng ta phân tích có yu t di truyn thì

o lưng ca hai bnh nhân không ưc xem là c lp.

1. Lí thuyt ca kim nh t

Cho hai qun th c lp 1 và 2, v$i ch s trung bình

và

, và phương sai

. Chúng ta mun ánh giá  khác bit gia hai qun th. Nhưng chúng ta không bit

các giá tr này.

 tìm hiu xem

và

có khác nhau hay không, chúng ta ly mu t& hai

qun th ó. Gi s chúng ta ly ngu nhiên

i tưng t& qun th 1, và

i tưng

t& qun th 2. Sau khi o lưng bin s, chúng ta có kt qu như sau:

Chng trình hun luyn y khoa – YKHOA.NET Training – Nguyn Vn Tun 2

Nhóm 1 Nhóm 2

S i tưng

Trung bình

Phương sai

 lch chun

Xin nh'c l"i, chúng ta mun tìm hiu  khác bit gia hai qun th (ch không

phi gia hai nhóm mu). Mc ích này có th phát biu bng hai gi thuyt như sau:

Gi thuyt vô hiu Ho:

1 2

µ µ

Gi thuyt chính H1:

1 2

µ µ

≠

Gi

∆

(

, hai gi thuyt trên cng có th phát biu như sau:

Ho: ∆ = 0

H1: ∆ ) 0

Trong iu kin không bit các giá tr ca qun th

và

, ư$c s thích hp nht

qun th chính là hai s trung bình

và

tính t& mu 1 và mu 2. Và, ư$c tính 

khác bit ∆ chính là  khác bit gia hai s trung bình:

d =

(

[1]

Nhưng vì ly mu, cho nên d có th bin thiên t& mu này sang mu khác, và vn  là

tìm phương sai ca d. Lí thuyt xác sut cho chúng ta bit rng phương sai ca khác bit

gia hai bin bng t*ng phương sai ca hai bin tr& cho 2 ln hip bin, tc là:

var(a – b) = var(a) + var(b) – 2×cov(a,b)

Trong ó, “var” là vit t't ca variance (phương sai), và “covar” là vit t't ca covariance

(hip bin). Hip bin phn nh  tương quan gia hai bin. Nhưng nu hai bin hoàn

toàn c lp, thì hip bin s là 0, và công thc trên ơn gin thành:

var(a – b) = var(a) + var(b)

Chng trình hun luyn y khoa – YKHOA.NET Training – Nguyn Vn Tun 3

Áp dng công thc này, chúng ta có th ư$c tính phương sai cho d trong [1] như sau

(Tôi s kí hiu phương sai bng s bình phương):

2sssd+= [2]

T& ó,  lch chun ca d là:

1sssd+= [3]

Nhưng vì nhng ư$c s u d+a vào s c, mu, cho nên chúng ta phi “iu chnh” bng

cách chia phương sai cho s c, mu:

SEd+= [4]

Nu phương sai ca hai nhóm bng nhau (tc

2 2 2

1 2

sss

= =

), phương trình [4] ơn gin

thành:

1 2

1 1

SE s

n n

= + [5]

Kim nh t ơn gin là t s ca d trên SEd, hay c th hơn:

= [6]

Có th xem công thc [5] như là t s ca “tín hiu” (signal) và “nhiu” (SEd).

Tht vy, d phn nh  khác bit gia hai nhóm, và SEd phn nh  nhiu ca d.

Thành ra, nu t s t cao, chúng ta có bng chng  nói tín hiu nhiu hơn nhiu (tc có

ý ngh%a thng kê); nu t s t thp dư$i 1 ch!ng h"n, chúng ta có bng chng  phát biu

tín hiu thp hơn nhiu và do ó  khác bit không có ý ngh%a thng kê.

Nhưng “cao” là cao bao nhiêu  có th nói là có ý ngh%a thng kê?  tr li câu

hi này, chúng ta quay tr v v$i gi thuyt. Nu gi thuyt vô hiu Ho là s+ tht (tc

không có khác bit gia 2 qun th), thì s+ phân phi ngu nhiên ca t như th nào. May

m'n thay, ã có nhà thng kê hc tr li câu hi này: ó là ông William Gossett, ngưi

phát kin kim nh t. Theo chng minh ca Gossett, nu hai qun th không khác nhau,

thì giá tr ca t tùy thuc vào s c, mu (hay nói theo ngôn ng thng kê hc là bc t do

– degrees of freedom). S bc t+ do (kí hiu) ưc tính bng công thc sau ây:

Chng trình hun luyn y khoa – YKHOA.NET Training – Nguyn Vn Tun 4

df =

( 2

Bng 1 sau ây trình bày t s t cho t&ng bc t+ do và khong xác sut mà t s t có th

dao ng ngu nhiên:

Bng 1. T s t cho tng bc t do nu gi thuyt vô hiu Ho úng

Bc t do (df) Xác sut 95% t s t s

dao ng trong khong

Xác sut 99% t s t s

dao ng trong khong

5 -2.57 n 2.57 -4.03 n 4.03

10 -2.23 n 2.23 -3.17 n 3.17

14 -2.14 n 2.14 -2.98 n 2.98

16 -2.12 n 2.12 -2.92 n 2.92

18 -2.10 n 2.10 -2.88 n 2.88

20 -2.08 n 2.08 -2.84 n 2.84

24 -2.06 n 2.06 -2.80 n 2.80

30 -2.04 n 2.04 -2.75 n 2.75

34 -2.03 n 2.03 -2.73 n 2.73

40 -2.02 n 2.02 -2.70 n 2.70

50 -2.01 n 2.01 -2.68 n 2.68

60 -2.00 n 2.00 -2.66 n 2.66

70 -2.00 n 2.00 -2.65 n 2.65

80 -2.00 n 2.00 -2.64 n 2.64

90 -1.99 n 1.99 -2.64 n 2.64

100 -1.98 n 1.98 -2.62 n 2.62

500 -1.96 n 1.96 -2.58 n 2.58

1000 -1.96 n 1.96 -2.58 n 2.58

Do ó, nu t s t tính toán t& công thc [6] nm ngoài khong tin cy trên ây, chúng ta

có th nói rng  khác bit gia hai qun th có ý ngh%a thng kê (thut ng ting Anh là

“statistically significant”).

2. Kim nh t vi bin c hoán chuyn logarít

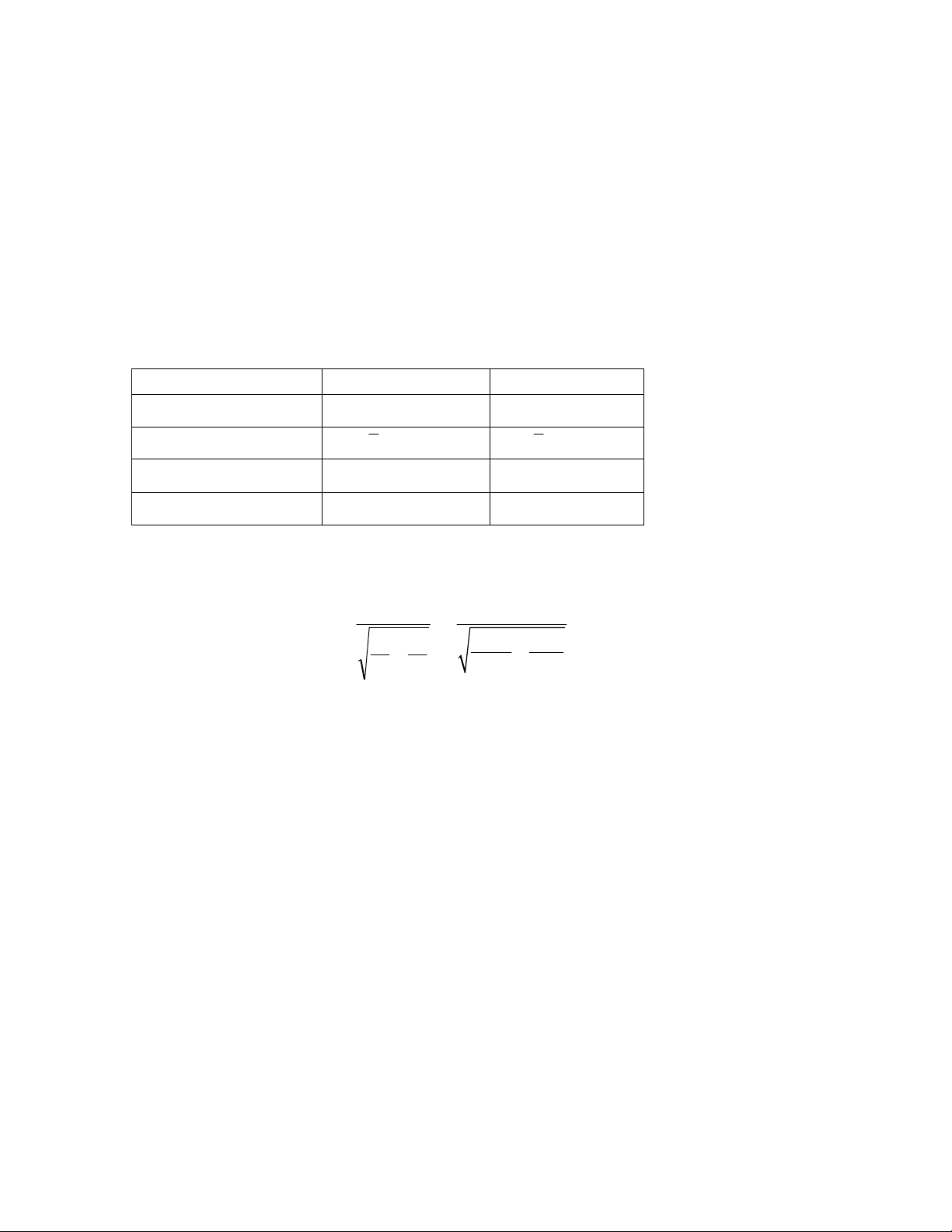
Ví d 1. Mt nghiên cu nhm so sánh n#ng  lysozyme gia hai nhóm bnh

nhân (t"m gi là nhóm 1 và nhóm 2). Nhóm 1 g#m 29 bnh nhân, và nhóm 2 g#m 30

bnh nhân, tu*i t& 20 n 60. N#ng  lysozyme (mg/L) như sau và có th tóm lưc

trong Bng 2:

Chng trình hun luyn y khoa – YKHOA.NET Training – Nguyn Vn Tun 5

Nhóm 1: 0.2, 0.3, 0.4, 1.1, 2.0, 2.1, 3.3, 3.8, 4.5, 4.8, 4.9, 5.0, 5.3,

7.5, 9.8, 10.4, 10.9, 11.3, 12.4, 16.2, 17.6, 18.9, 20.7, 24.0, 25.4,

40.0, 42.2, 50.0, 60.0

Nhóm 2: 0.2, 0.3, 0.4, 0.7, 1.2, 1.5, 1.5, 1.9, 2.0, 2.4, 2.5, 2.8, 3.6,

4.8, 4.8, 5.4, 5.7, 5.8, 7.5, 8.7, 8.8, 9.1, 10.3, 15.6, 16.1, 16.5,

16.7, 20.0, 20.7, 33.0

Bng 2. Nng  lysozyme  bnh nhân nhóm 1 và nhóm 2

Nhóm 1 Nhóm 2

S i tưng

= 29

= 30

Trung bình

= 14.31

= 7.68

Phương sai

= 247.8

= 61.6

 lch chun

= 15.7

= 7.8

Áp dng công thc [6], chúng ta có t s t như sau:

= =

14.31 7.68

29 30

−

= 2.03

V$i bc t+ do df = 29+30-2 = 57, và nu hai nhóm không khác nhau, chúng ta kì vng

rng t s t dao ng t& -2.00 n 2.00 (theo Bng 1). Nhưng t s t quan sát ưc nm

ngoài khong tin cy này, nên chúng ta có th phát biu rng  lysozyme ca hai nhóm

khác nhau.

Nhưng kt qu và kt lun trên có th sai! Nhìn qua tóm t't trình bày trong Bng

2, chúng ta chú ý phương sai ca nhóm 1 cao gp 4 ln so v$i nhóm 1. Ngoài ra, phương

sai có xu hư$ng bin thiên theo s trung bình: nhóm có s trung bình cao cng là nhóm

có phương sai cao.  lch chun ca nhóm 1 cao hơn nhóm 2 gp hai ln.

Chúng ta cng chú ý rng  lch chun ca hai nhóm cao hơn s trung bình.

iu này hàm ý cho bit s liu lysozyme không tuân theo lut phân phi chun, và phân

tích trên ã vi ph"m gi nh thng kê. Chúng ta th xem qua phân phi ca lysozyme

trong nhóm 1 và nhóm 2 như sau:

Lâm sàng thống kê: Bài 5. Kiểm định t và hoán chuyển số liệu - Nguyễn Văn Tuấn

Chủ đề:

Tài liệu liên quan

Tài liêu mới

AI tóm tắt

Giới thiệu tài liệu

Đối tượng sử dụng

Từ khoá chính

Nội dung tóm tắt

Hỗ trợ

Phương thức thanh toán

Theo dõi chúng tôi