30
CHƯƠNG 2
CƠ SỞ LÝ THUYẾT CHUNG VỀ PHÂN TÍCH ĐỘNG HỌC
CỦA VẬT RẮN TRONG KHÔNG GIAN
2.1 Ma trận cosin chỉ hướng
2.1.1 Định nghĩa ma trận cosin chỉ hướng của vật rắn
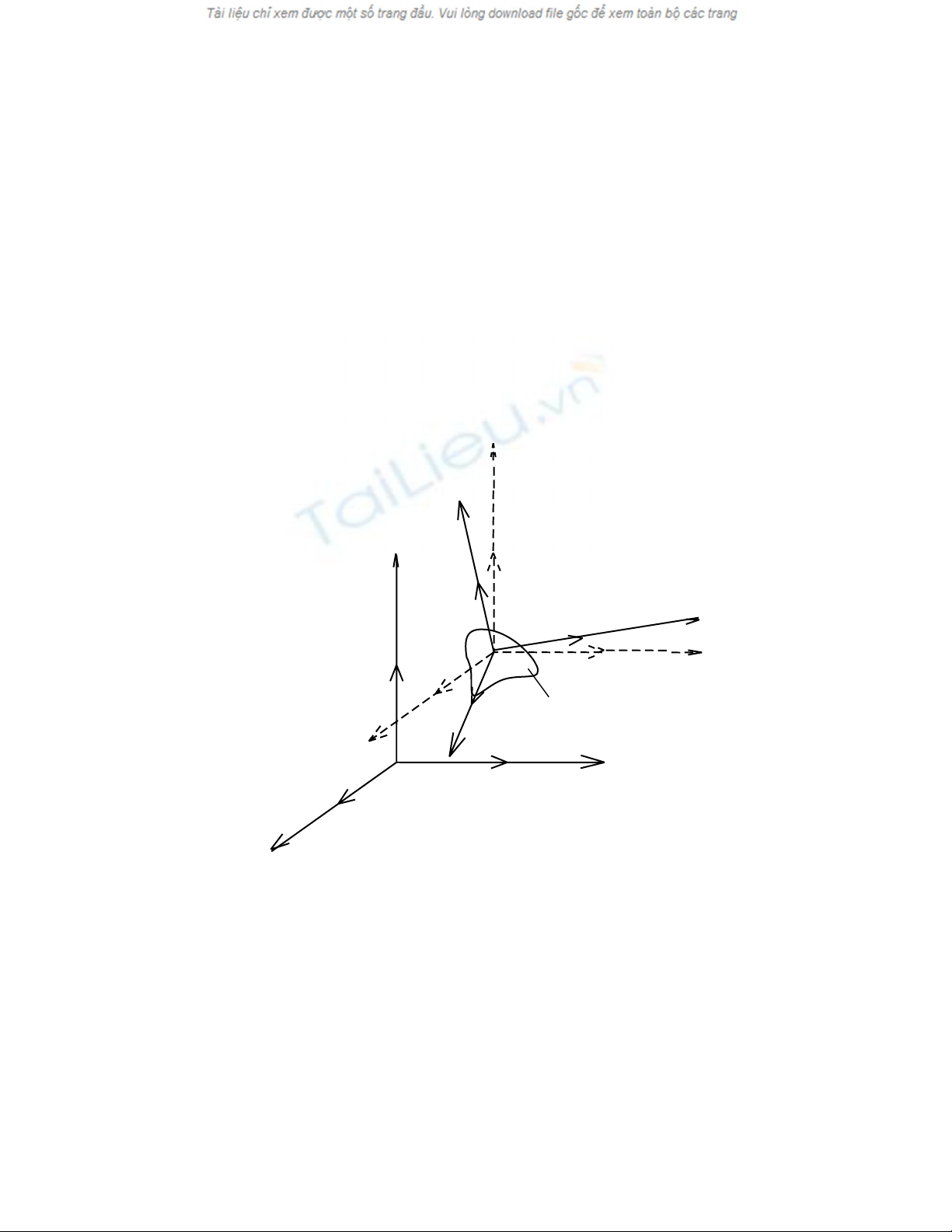
Cho vật rắn B và hệ quy chiếu R = { )0(
3
)0(
2
)0(
1e,e,e
r
r
r
}. Trong đó )0(
3
)0(
2
)0(
1e,e,e
r
r
r
là
ba véc tơ đơn vị trên các trục Ox0, Oy0, Oz0 . Ta gắn chặt vật rắn vào một hệ
quy chiếu R = { 321 e,e,e
r
r
r
}, với 321 e,e,e
r
r
r
là ba véc tơ đơn vị trên các trục Az,
Ay, Az, (Hình 2.1).
`
Định nghĩa ma trận vuông cấp ba
A=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
3
)0(
32
)0(
31
)0(
3
3
)0(
22
)0(
21
)0(
2
3
)0(
12
)0(
11
)0(
1
e.ee.ee.e
e.ee.ee.e
e.ee.ee.e
rrrrrr
rrrrrr
r
r
r
r
r
r
(2.1)
được gọi là ma trận cosin chỉ hướng của vật rắn B đối với hệ quy chiếu R0.
A
O
Hình 2.0
y0
z0
x0
B
y1
z1
x1
z
y
)0(
1
e
r
)0(
3
e
r
)0(
2
e
r
2
e
r
1
e
r
3
e
r
x1
31
Nếu ta đưa vào ký hiệu
aij = e
r)0(
i.j
e
r
= cos( e
r)0(
i.j
e
r
), với (i,j = 1,2,3) (2.2)
Thì ma trận cosin chỉ hướng (2.1) có dạng
A =
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
333231
232221
131211
aaa
aaa
aaa
(2.3)
Từ định nghĩa trên, trong hệ quy chiếu R0 ta có các hệ thức hiên hệ:
)0(
331
)0(
221
)0(
1111 eaeaeae
r
r
r
r
++=
)0(
332
)0(
222
)0(
1122 eaeaeae
r
r
r
r
++= (2.4)
)0(
333
)0(
223
)0(
1133 eaeaeae
r
rrr ++=
Nếu ta ký hiệu ei là ma trận cột gồm các phần tử của véc tơ i
e
r trong hệ qui
chiếu R0.
Ta có:
e1
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
31
21
11
a
a
a
, e2
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
32
22
12
a
a
a
, e3
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
33
23
13
a
a
a
(2.5)
Tìm ma trận cosin chỉ hướng (2.3) có dạng:
A = [e1, e2, e3] (2.6)
Ma trận cosin chỉ hướng A còn được gọi là ma trận quay của vật rắn.
2.1.2 Một vài tính chất cơ bản của ma trận cosin chỉ hướng
a) Tính chất 1: ma trận cosin chỉ hướng là ma trận trực giao.
Theo công thức (2.6):
A = [e1, e2, e3]
Ma trận cosin chỉ hướng A là ma trận cột có ba cột là ba véc tơ trực chuẩn.
Do đó A là ma trận trực giao.
Do tính chất của ma trận cosin chỉ hướng là ma trận trực giao nên A.AT = E.
Từ đó nhận được 6 phương trình liên hệ giữa các thành phần của ma trận
cosin chỉ hướng như sau:
32
1aaa 2
31
2
21
2
11 =++ 0aaaaaa 323122211211 =
+
+
1aaa 2
32
2
22
2
12 =++ 0aaaaaa 333123211311 =
+
+
1aaa 2
33
2
23
2
13 =++ 0aaaaaa 333223221312 =
+
+
Do vậy chỉ có 3 thành phần của ma trận cosin chỉ hướng là độc lập.
b)Tính chất 2: Định thức của ma trận cosin chỉ hướng det(A)=1
Từ hệ thức A.AT = E ta suy ra:
det(A.AT)= det(A). det(AT)= det(E)=1
Do: det(A)=det(AT) nên ta có det(A)= 1
±
. Ta có thể chứng minh det(A)=1.
c)Tính chất 3: Ma trận cosin chỉ hướng có ít nhất một trị riêng 1
1=λ
2.1.3 Ý nghĩa của ma trận cosin chỉ hướng của vật rắn
Xét một hệ qui chiếu R0 và R có cùng gốc O. Trong đó hệ qui chiêú R0
≡
Ox0y0z0 là hệ qui chiếu cố định, Hệ qui chiếu R
≡
Oxyz gắn liền với vật rắn B.
Lấy điểm P bất kỳ thuộc vật rắn B. Vị trí của điểm P được xát định bởi vectơ
định vị OP =p
r.(Hình 2.1)
Hình 2.1
Ký hiệu các toạ độ của điểm P trong hệ qui chiếu động Oxyz là xp, yp, zp, các
toạ độ của điểm P toạ độ hệ qui chiếu cố định Ox0y0z0 là 0
p
x, y 0
p, z 0
p.
Ta có hệ thức sau:
)0(
3
)0(
p
)0(
2
)0(
p
)0(
1
)0(
pp e.ze.ye.xr
r
rrr
+
+= (2.7)
z
x
y0
y
x0
z0
)0(
2
e
r
)0(
3
e
r
)0(
1
e
r
2
e
r
3
e
r
1
e
r
P
B
33
3p2p1pp e.ze.ye.xr
r
rrr ++= (2.8)
Thế các biểu thức (2.4) vào hệ thức (2.8) ta được:
+
+
+= )e.ae.ae.a(xr )0(
331
)0(
221
)0(
111pp
r
rrr (2.9)
+
+
+)e.ae.ae.a(y )0(
332
)0(
222
)0(
112p
r
r
r
)e.ae.ae.a.(z )0(
333
)0(
223
)0(
113p
r
r
r
+
+
Hay:
+
+
+= )z.ay.ax.a(er p13p12p11
)0(
1p
rr (2.10)
+
+
+)z.ay.ax.a(e p23p22p21
)0(
2
r
)z.ay.ax.a(e p33p32p31
)0(
3
+
+
r
So sánh các biểu thức (2.7), và (2.10) ta suy ra hệ phương trình:
p13p12p11
)0(
pz.ay.ax.ax
+
+=
p23p22p21
)0(
pz.ay.ax.ay
+
+= (2.11)
p33p32p31
)0(
pz.ay.ax.az
+
+=
Hệ phương trình (2.11) có thể viết lại dưới dạng ma trận như sau;
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
p
p
p
333231
232221
131211
)0(
p
)0(
p
)0(
p
z
y
x
.
aaa
aaa
aaa
z
y
x
(2.12)
Từ hệ phương trình (2.12) ta rút ra kết luận sau:
Ma trận cosin chỉ hướng A biến đổi các toạ độ của điển P bất kỳ thuộc vật
rắn trong hệ quy chiếu động Oxyz sang các toạ độ của điểm P đó trong hệ quy
chiếu cố định Ox0y0z0
2.2 Các ma trận quay cơ bản
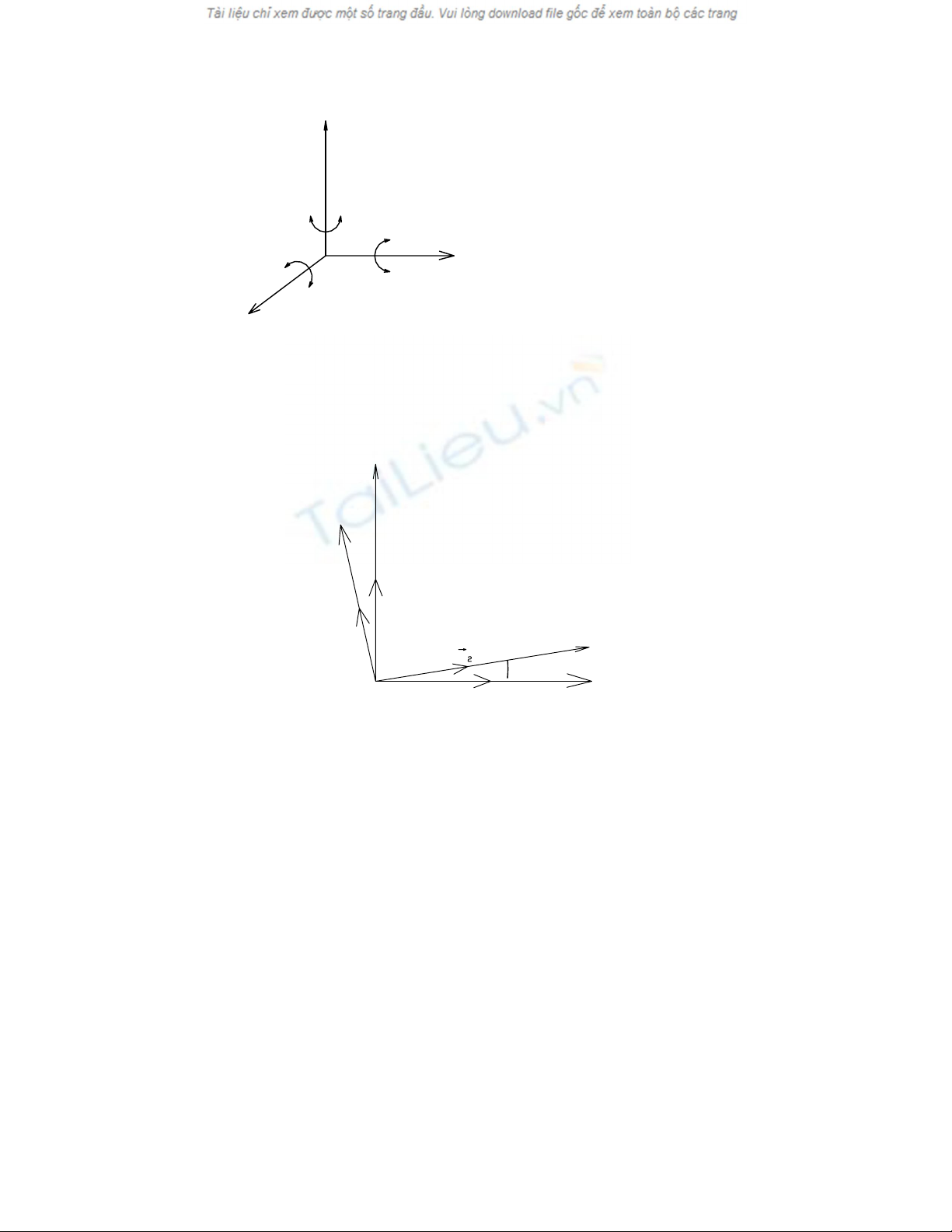
Ta quy ước hướng quay đơn là hướng ngược chiều kim đồng hồ như hình vẽ (
Hình 2.2)
34
Các phép quay quanh trục x,y,z của hệ toạ độ vuông góc Oxyz được là phép
quay cơ bản.
Ta tìm ra ma trận quay của phép quay quanh trục một góc ϕ (Hình 2.3).
Theo công thức định nghĩa (2.1) ta có:
Ax0(ϕ) =
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
3
)0(
32
)0(
31
)0(
3
3
)0(
22
)0(
21
)0(
2
3
)0(
12
)0(
11
)0(
1
e.ee.ee.e
e.ee.ee.e
e.ee.ee.e
rrrrrr
rrrrrr
r
r
r
r
r
r
(2.13)
Ax0(ϕ) =
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
ϕϕ
ϕ−ϕ
cossin0
sincos0
001
` (2.14)
Ma trận (2.14) được gọi là ma trận quay của phép quay cơ bản quanh trục x0
bằng cách tương tự ta xác định được các ma trận quay cơ bản quanh các trục
y0 và z0 (Hình 2.4).
y
e
z
Hình 2.3
y0
z0
)0(
3
e
r
)0(
2
e
r
3
e
r
H×nh 2.2
z
O
x
y
θ
ϕ