Sử dụng bộ điều khiển nơron được tối ưu bằng giải thuật di truyền trong mạch truyền
thẳng điều khiển robot bằng phương pháp tính momen.
Tác giả:
Nguyễn Trần Hiệp - Học viện Kỹ thuật Quân sư.
Phạm Thượng Cát - Viện Công nghệ Thông tin.
Tóm tắt:
Phương pháp tính momen là một phương pháp phổ biến trong điều khiển robot hiện đại. Nó cho phép loại bỏ
được tất cả các thành phần phi tuyến và liên kết chéo trong robot. Nhược điểm của phương pháp này là các tham số
phi tuyến thường không được ước lượng chính xác và quá trình tính toán phức tạp đòi hỏi thời gian thực. Vì vậy
trong thực tế dao động và quá chỉnh thường xuyên xuất hiện khi điều khiển bằng phương pháp tính momen. Mạng
nơron và thuật di truyền có thể cho phép khắc phục được những nhược điểm này. Bài báo này giới thiệu việc sử
dụng mạng nơron được tối ưu bằng thuật di truyền thực hiện tính toán chính xác các tham số phi tuyến và liên kết
chéo của hệ robot. Hệ điều khiển được kiểm chứng bằng MATLAB SIMULINK 6.0 trên cánh tay máy hai bậc tự do.
Abstract:
The computed torque method is very popular in modern in rorbot control. The computed torque method involes
computation and cancellation of all non-linearities and cross-coupling terms. The disadvantage of this method is the
misestimation of non – linear parametes and the computation complexity of the real-time implementation. In practice
oscillation and overshoot always occurs when computed torque method applicated. The drawbacks of this method
are overcome by Neural network and genetic algorithm. This paper presents a neural netwokr optimied by genetic
algorithm to correct computation of all non-linearities and cross-coupling terms.. The controller was tested through
simulation by MATLAB simulink 6.0 on the 2 – DOF manipulator.
1. Đặt vấn đề.
Phương pháp tuyến tính hoá phản hồi hay còn
được gọi là phương pháp tính momen là một phương
pháp điều khiển hiện đại trong công nghiệp robot. Bộ
điều khiển được thực hiện trên cơ sở tách riêng mô
hình động lực học của robot thanh hai phần tuyến tính
và phi tuyến, do đó các thành phần như trọng lực, lực
ma sát, momen hướng tâm, lực Coriolis .v.v. sẽ được
bù đủ [18] [20]. Khi đó, bộ điều khiển PD hay PID
được sử dụng để điều khiển vị trí của robot tiệm cận
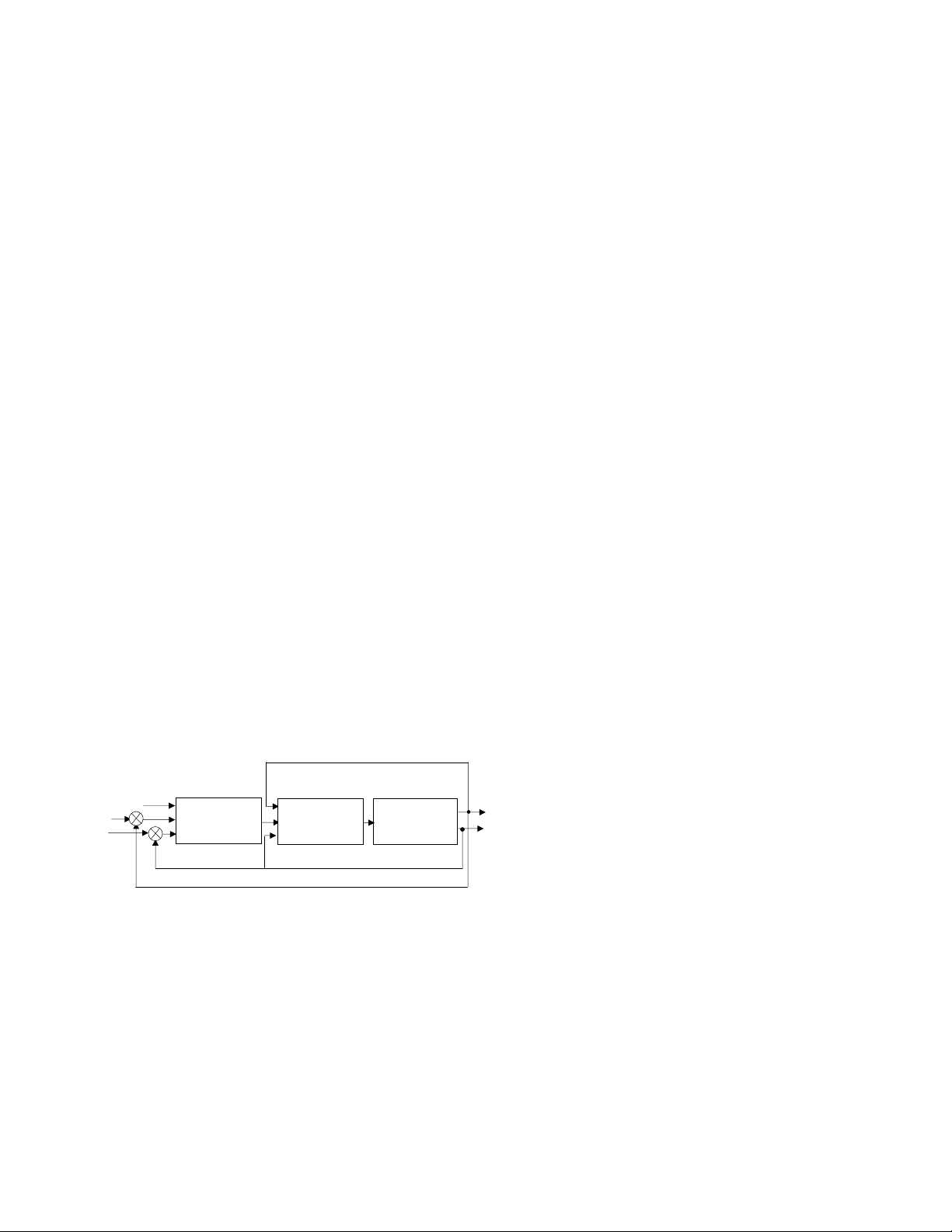
với quỹ đạo mong muốn. Sơ đồ hệ điều khiển tính
momen được biểu diễn như sau:
Dựa vào sơ đồ trên ta viết được phương trình:
q),qh(H(q)uτ&
+= (11)
eKde(τK eKqu &&&
D
t
0
IPd τ+
∫
++= ) (1.2)
Trong đó e = qd – q;
qqe &&& −= d
KI , KP, KD là các ma trận đường chéo xác định
dương. Nếu ma trận H và vector h được xác định
chính xác thì momen τ cũng được xác định chính xác
và robot sẽ được điều khiển bám sát quỹ đạo mong
muốn. Vì ma trận H là xác định dương và khả đảo
nên từ hình 1 và công thức 1.1 vòng điều khiển kín có
dạng:
uq
=
&& (1.3)
Như vậy hệ kín có dạng là n tích phân riêng biệt
điều khiển độc lập n khớp và tín hiệu điều khiển độc
lập tại mỗi khớp sẽ là:
iDi
t
0
i
iIPidi ekdτ(τe k
i
ekq
i
u&&& +
∫
++= )
(1.4)
Khi ma trận H và vector h giả thiết được xác định
chính xác, hệ thống sẽ là ổn định tiệm cận nếu các hệ
số k
Di, kPi, kIi và thậm chí không còn xuất hiện dao
động và độ quá chỉnh trong hệ thống [18]. Thực tế,
ma trân H và vector h không thể biết được chính xác
mà chúng ta chỉ nhận được một giá trị ước lượng H
~
và h
~
( HH ≠
~
;hh ≠
~
). Thay thế các giá trị ước lượng H
~
và h
~
vào phương trình động lực học của robot ta
nhận được:
(
)
(
)
h-hHuHq ~~ 1-1- H+=
&& (1.5)
Rõ ràng phương trình này khác với phương trình
1.3 và vì vậy luật điều khiển tính momen như trên sẽ
gây ra sai số. Trong thực tế phương pháp này phần
nào khắc phục được tính không xác định của mô hình
vì hệ thống đã tính đến các thành phần phi tuyến của
đối tượng điều khiển và sai số của điều khiển phụ
thuộc vào mức độ sai lệch giữa H(θ) và )
~
(θH;
và . Một khó khăn nữa của phương pháp tính
momen là đòi hỏi thực hiện ở chế độ thời gian thực.
Việc tính toán như vậy đòi hỏi những hệ tính toán
)qh(q, &
)q(q,h &
~
H
ình 1: Phư
ơ
n
g
p
há
p
đ
iều khiển tính momen
qd τ
q
&
q
Robot
u Tính:
q),qh(H(q)u &
+
∫++
+
eKdteK
K
D
d
I
P
&
&
d
&
+eq
&
q
&
d
q
&
1
phức tạp và đắt tiền. Để nâng cao chất lượng của điều
khiển theo phương pháp phản hồi tuyến tính trong kỹ
thuật điều khiển nói chung hay trong điều khiển robot
nói riêng đã có nhiều nghiên cứu được đề xuất. Chủ
yếu tập trung vào việc tính toán một cách chính xác
và nhanh chóng các giá trị ước lượng )
~
(θH, và
các hệ số K
)q(q,h &
~
P, KI, KD của bộ điều khiển. Chẳng hạn
như Keigo và Mohamad sử dụng ANN hay như đề
xuất của Nguyễn Công Định sử dụng GAs và Fuzzy
để xác định các hệ số KP, KI, KD tối ưu của bộ điều
khiển [20]. Một phương pháp nữa là sử dụng ANN để
xác định chính xác các giá trị ước lượng )
~
(θH,)
.Rodi và R.Safaric đã sử dụng [7][16][17]. Các
phương pháp sử dụng ANN như đã trình bày ở trên
đều sử dụng thuật học BP. Vấn đề chính là ở chỗ
thuật học BP và các thuật học khác sử dụng nguyên lý
gradient suy giảm không có khả năng hội tụ toàn cục.
Chỉ có giải thuật di truyền (GAs) mới có khả năng
làm cho quá trình học của ANN tiến tới hội tụ toàn
cục. Bài báo này đề xuất một phương pháp sử dụng
mạng nơron nhân tạo (ANN) được học bằng GAs để
xác định chính xác các tham số phi tuyến H
q(q,h &
~
mà M
~
và )q(q,h &
~
khi điề khiểot bằng phương pháp tính momen.
Khi đó đối tượng điều khiển (robot) được coi như là
một hệ tuyến tính và các hệ số K
un rob
P, KI, KD, đảm bảo
cho hệ ổn định và có tốc độ hội tụ nhanh trong
trường hợp này có thể được xác định như với hệ điều
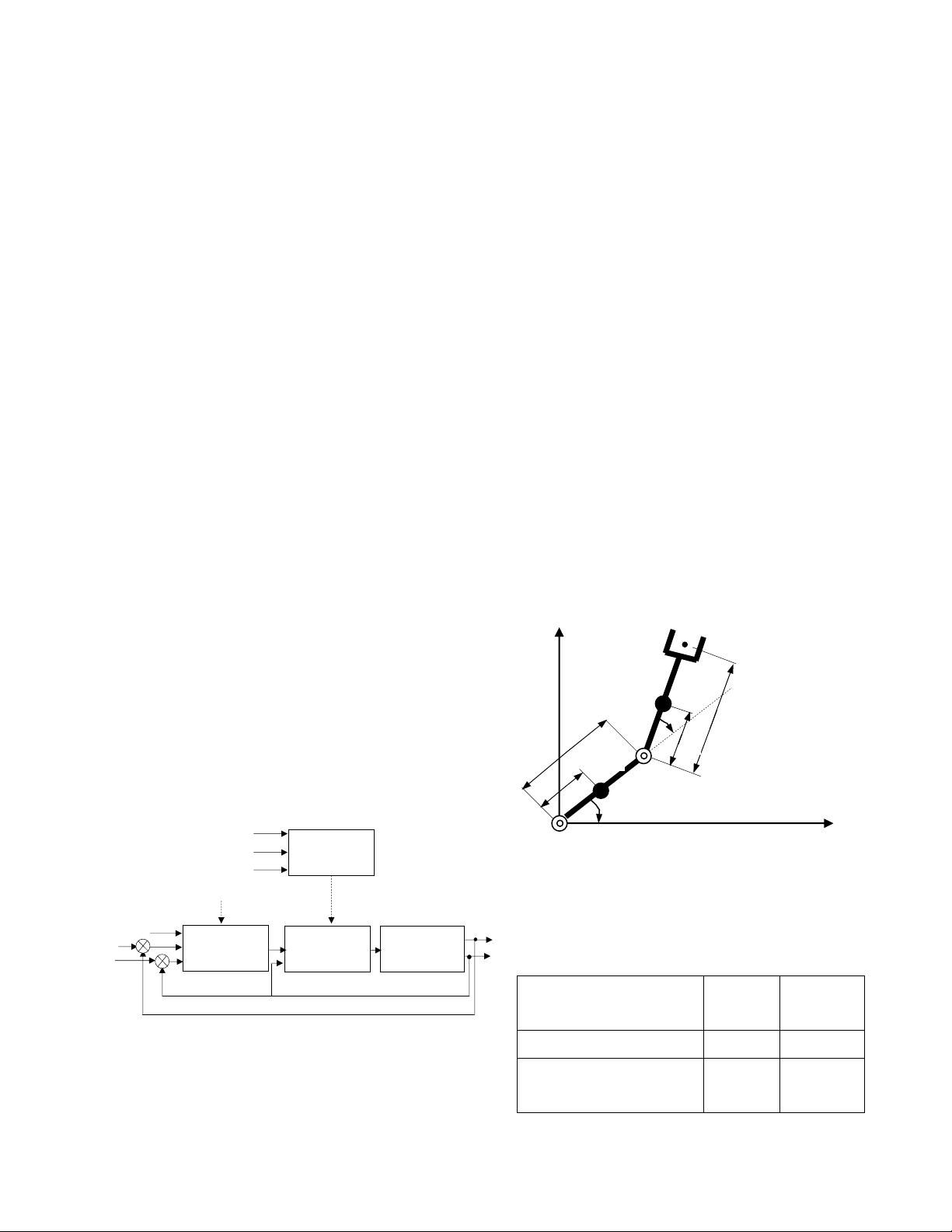
khiển PID cho các đối tượng tuyến tính. Hình 1.2 mô
tả hệ điều khiển tính momen có sử dụng ANN được
tối ưu tham số bằng GAs để bù các thành phần không
xác định của đối tượng.
Số đầu vào của ANN như trên hình 1.2 chính là
các biến trạng thái và đạo hàm của chúng, tín hiệu u
trên đầu ra của bộ lấy tích phân, tín hiệu điều khiển τ
tác động lên đối tượng được tạo ra trên đầu ra của
ANN. Thuật di truyền (GAs) đóng vai trò giám sát sẽ
thay đổi các trọng số liên kết của ANN để tìm được
tập hợp trọng số tối ưu sao cho chất lượng của điều
khiển là tốt nhất.
2. Điều khiển robot hai bậc tự do sử dụng ANN
được tối ưu bằng GAs theo phương pháp tính
momen.
Xét một mô hình robot hai bậc tự do được mô tả
như hình 1.3.
Phương trình chuyển động của robot hai bậc tự do
có sơ đồ như hình 1.3 được viết như sau:
τ),h()H( =θθ+θθ &&& (1.6)
[
]
2
T
2Rτ1∈ττ= ,là momen của khớp robot.
[
]
2
T
21 Rθ∈θθ= ,Biểu diễn góc quay của khớp robot.
(
)
2x2
RH ∈θ là ma trận quán tính của robot có các phần
tử được cho như sau:
(
)
⎥
⎦
⎤
⎢
⎣
⎡+++++= 2
θcos
g2
l
n1
2l
2
g2
l
2
n1
l
2
m
2
g1
l
1
m
2
I
1
I
11
H (1.7)
()
⎥
⎦
⎤
⎢
⎣
⎡θ++== 22g1n
2
2g2221
12 cosll2lmIHH (1.8)
2
2g2222 lmIH += (1.9)
I1, I2 là momen quán tính của khớp thứ nhất và khớp
thứ hai
lg1, lg2 ;ag khoảng cách từ khớp thứ nhất và khớp thứ
hai đến trọng tâm của khớp một và hai.
ln1; ln2 là chiều dài của khớp một và khớp hai.
m1; m2 là khối lượng của khớp một và khớp hai.
mm1; mm2 là khối lượng của động cơ khớp một và
khớp hai.
Vector biểu diễn thành phần của lực
2
R)qh(q, ∈
&
Coriolis và trọng lực của hai khớp:
22122g1n21 2llmh θθ+θθ−= &&& ))((sin (1.10)
122g1n22 llmh θθ= &
)(sin (1.11)
Với các tham số của robot được cho như sau:
Khớp thứ
nhất
Khớp thứ
hai
Trọng lượng khớp mij [kg] 50.0 50.0
Trọng lượng của động cơ
mmi [kg]
5.0 5.0
Hình 1.3: Biểu diễn robot hai bậc tự do
θ
2
lg1
ln1
y
khớ
p
I2, m2
ln2
lg2
I1, m1
kh
ớp
θ
1
x
e Thuật học
(GAs)
e
&&
Hình 2: H ệ điều khiển tính momen d ùng
ANN v à thuật học G As
e
&
Hệ số KP, KI, KD Chỉnh trọng số wi
j
Mạng Nơron
(ANN)
qd τ
q
&
q
Robot
∫++
++
eKdteK
eKq
D
d
I
P
&
&&
d
q
&&
d
q
&
2

Quán tính của khớp Ili
[kg.m2]
10.0 10.0
Quán tính của động cơ I
mi
[kg.m2]
0.01 0.01
Khoảng cách li [m] 1.0 1.0
Khoảng cách lgi [m] 0.5 0.5
Hệ số giảm tốc của hộp số
kri
100 100
Quỹ đạo mong muốn của robot được giả thiết là
hàm thời gian của vị trí, vận tốc và gia tốc góc [21]:
θd1(t) = 0.5 cos (πt); θd2(t) = 0.5 sin (πt) + 1.0
)(.)( t50t
1d ππ−=θ sin
&; )(.)( t50t
2d ππ=θ cos
&
)(.)( t50t 2
1d ππ−=θ cos
&& ; )(.)( t50t 2
2d ππ−=θ sin
&&
Mục đích của bài toán điều khiển là tìm momen tác
động lên các khớp của robot để robot chuyển động
đến vị trí mong muốn thoả mãn các yêu cầu của quá
trình điều khiển. Sai số của mô hình robot, sự thay
đổi các tham số của robot, vị trí và đạo hàm của tín
hiệu phản hồi được dùng để tính toán chính xác tín
hiệu điều khiển tác động lên robot. Do tính không xác
định của mô hình robot nên phương trình 1.6 được
viết:
τ),(h)(H =θθ+θθ &&&
~
~
(1.12)
)
~
(θH và là các giá trị ước lượng của H(θ) và
. Kết hợp 1.8; 1.9; 1.10và 1.11 ta có:
)q(q,h &
~
)qh(q, &
∫
+++=
t
0
iPdd dteKeKeKθθ &
&&&&
(1.13)
Tín hiệu e = [e1, e2]T
= [θd - θ] là các giá trị
sai lệch.
Khi )
~
(θH và ~hoàn toàn giống như
H(θ) và h(q, thì phương trình của vector sai lệch sẽ
thoả mãn phương trình tuyến tính sau:
)q(q,h &
)q
&
0dt
t
0
IPD =+++ ∫eKeKeKe &&&
(1.14)
Như vậy ta có thể chọn KP, KI, KD để hệ thống
này ổn định như mong muốn.
Hệ điều khiển khi đó được coi như là một hệ tuyến
tính, các hệ số KP, KI, KD lúc đó được chọn như khi
thiết kế bộ điều khiển PID với đối tượng tuyến tính
cho hệ nhiều đầu vào/ra. Các hệ số này có thể chọn
theo phương pháp dễ dàng nhất như phương pháp đặt
điểm cực.
Với ANN có cấu trúc 6-8-2 tức là có 6 nơron trên
lớp vào
[
]
222111 uu θθθθ && ,,,,, , 8 nơron tại lớp ẩn và 2
nơron trên đầu ra
[
. Với cấu trúc như trên hình
1.4 số lượng các liên kết của ANN sẽ là (7x8) + (9x2)
= 74. Hàm tác động của các nơron tại đầu vào là hàm
tuyến tính, tại lớp ẩn là hàm sigmoid lưỡng
]
cực và
obot trong trường hợp này có
ơ đồ cấu trúc như sau:
Cấu trúc mạng nơron được biểu diễn như sau:
21 ττ ,
của nơron tại lớp ra là hàm dấu bão hoà[10].
Hệ thống điều khiển r
s
Hình 1.4: Bộ điều k n sử dụng ANN và
thu
hiển tính mome
ậ
t h
ọ
c GAs
GAs
Q
muốn
d2
d2
d1
θ,θ
θθ
θθ
&&&
&&
&
uỹ đạo
mong
d2
d1 ,
d1 ,
ANN
+
+
+
+
+
+
+
+
+
+
u
1
+
+
KI1
u
2
KI2
e
&
KD1
KP1
∫edt
∫edt
KP2
KD2
Ro
bot
Chỉnh tr
ọ
n
g
Chỉnh tr
ọ
n
g
Wi j
1
1
Z2
Z3
Z4
Z5
Z6
Z7
τ
1
τ
2
Thuật học GAs
Ch
số Wi j
q
q
&
q
&&
qd
d
q
&
d
q
&&
ỉnh trọng
Lớp đầu ra
Lớp đầu vào Lớp ẩn
Hình 1.5: Cấu trúc ANN và thuật học GAs
3

Trong đó tập hợp đầu , zvào z = [z , z , z 5, z6, z7]
234
chính là tập hợp đầu vào
[
]
22 θ
&
,.
Tín hiệu điều khiển
[]
2
T
2Rτ1∈ττ= ,tìm được ph
2111 uu θθθ &,,,,
ải
thỏa mãn điều kiện làm việc th c tế của robot:
tìm được một giá trị τ tối
ủa giá trị sai
số trung bình bình phương [2] [3] [6]:
ự
maxmin ττ≤ (1.14)
Trong đó τ
τ≤
min và τmax phụ thuộc vào công suất của
động cơ điều khiển tại các khớp của robot bởi vì nếu
giá trị τ tối ưu tìm được nằm ngoài khoảng này thì
động cơ của robot không có khả năng tạo được tín
hiệu điều khiển. Giải thiết quỹ đạo mong muốn của
robot qd nằm trong vùng hoạt động cho phép của
robot. Điều này cho phép
ưu đảm bảo cho q →qd.
Để sử dụng GAs trong quá trình học của ANN,
hàm mục tiêu được chọn theo nghịc đảo c
⎪
⎩
⎪
⎨
⎧
≤
>
=
max
nÕu
max
nÕu
qq
qq
))((
1
0
))(,(
c
TqF
tq
i
chromsF
T u kỳ điều khiển.
C là ch
max
qlà giá trị tới hạn quy định vùng làm việc
giá trị ước lượng theo hàm mục
của cá th
ng trung
bình của các biếntrạng thái tại thời điểm TC.
của robot.
F(chromsi, q(t)) là
tiêu ể thứ i.
))((
1C
TqF là nghịgh đảo sai số bình phươ
222
1
1
))((
eee
qF
&&& ∆+∆+∆
; )()(
0CC TT eee &&&
=
C
T (1.15)
)()(
0CC TT eee −=∆
−
=∆ ;
)()(
0CC TT eee &&&&&& −=∆ là sai lệch giữa sai số cho phép
tại thời điểm TC và sai số thực tế tại thời điểm TC.
Chương trình mô phỏng được thực hiện trên
MATLAB 6.0 với các tham số của GAs được cho
ẫu sec
PC)
i min
t dấu) 17
à
P2 = 6. Kết quả mô phỏng được biểu diễn như sau:
như sau:
Chu kỳ điều khiển TC3 sec
Khoảng thời gian lấy m 10 m
Tỷ lệ liên kết chéo ( 0.5
Tỷ lệ biến đổi (Pm) 0.1
Giá trị giới hạn của trọng số Wi max, W ± 5
Số bit mã hóa nhị phân (có 1 bi
Kích thước của tập hợp (Psize) 300
Các giá trị của hệ số KP, KI, KD như đã nói ở trên
được xác định bằng phương pháp đặt điểm cực chọn
được Ki1 = 1; KP1 = 3; KD1 = 3; KI2 = 8; KD2 = 12 v
K
Biểu diễn góc dự định và góc thực tế tại khớp một
Biểu diễn vận tốc góc dự định và thực tế tại khớp
một
Biểu diễn của momen dự định và thực tế tại khớp một
4

Biểu diễn góc dự định và góc thực tế tại khớp hai
Biểu diễn vận tốc góc dự định và thực tế tại khớp
hai
Biểu diễn của momen dự định và thực tế tại khớp hai
Kết luận:
Trong bài báo này, tác giả đã trình bày phương
pháp khắc phục được những nhược điểm của phương
pháp điều khiển tính momen. Hệ điều khiển có đặc
trưng phi tuyến đượcđược đưa về hệ tuyến tính trên
cơ sở bù chính xác các thành phần phi tuyến là các
giá trị ước lượng )
~
(θH và . Phương pháp này
đảm bảo được độ chính xác và hội tụ của hệ điều
khiển. Độ chính xác và chất lượng của quá trình điều
khiển phụ thuộc vào độ chính xác của các giá trị ước
lượng
)q(q,h &
~
)
~
(θH và và sự lựa chọn các hệ số K
)q(q,h &
~
P,
KI, KD của bộ điều khiển PID. Tác giả đề xuất một
phương pháp sử dụng ANN được tối ưu bằng GAs để
xác định chính xác các giá trị ước lượng )
~
(θH và
. Các kết quả mô phỏng trên tay máy hai bậc tự
do cho thấy rằng phương pháp mà tác giả đề xuất ở
trên có thể là một đóng góp nhằm làm phong phú hơn
các thuật học của ANN cũng như sự phong phú khi
sử dụng ANN vào các quá trình điều khiển nói chung.
)q(q,h &
~
Tài liệu tham khảo:
[1] Nguyễn Trần Hiệp, Phạm Thượng Cát-
Genetic Algorithm and its applications in Control
Engineering.
[2] Nguyễn Trần Hiệp, Phạm Thượng Cát- Nghiên
cứu bài toán dao động con lắc ngược sử dụng thuật
Gen bằng MATLAB. Hội thảo toàn quốc về phát
triển Phát triển công cụ tin học trợ giúp cho giảmg
dạy và nghiên cứu ứng dụng toán học – hà nội 4/199,
trang 326-334
[3] Nguyễn Trần Hiệp, Phạm Thượng Cát -
(1999) - Điều khiển con lắc ngược bằng phương pháp
trượt sử dụng mạng nơron được tối ưu bằng thuật gen
tr 30 – 38 Tạp chỉ KHKT số 90 năm 2000 - Học viện
Kỹ thuật Quân sự
[4] Nguyến Thanh Thuỷ, Trần Ngọc Hà, (1999)
Tích hợp kỹ thuật mạng nơron và giải thuật di truyền
trong phân tích dữ liệu. Tạp chí tin học và điều khiển
học T15, S.2
[5] Trần Văn Hãn - Đại số tuyến tính trong kỹ
thuật – Nhà xuất bản Đại học và trung học chuyên
nghiệp 1978.
[6] A. Haeussler, K. C. Ng Y. Li, D. J. Murray-
Smith, and K. C. Sharman - Neurocontrollers
designed by a genetic algorithm.
In Proc. First IEE/IEEE Int. Conf. on GA in Eng.
Syst.: Innovations and Appl., pages 536-542,
Sheffield, U.K., September 1995.
[7] Ales Hace, Riko Safaric, Karel Jezernik -
Faculty of Electrical Engineering and computer
Sciences University of Maribor Slovernia -Artificial
5









![Robot song song P2: [Thêm từ mô tả hấp dẫn, ví dụ: Hướng dẫn chi tiết, Cách chế tạo hiệu quả]](https://cdn.tailieu.vn/images/document/thumbnail/2010/20100323/tanlang/135x160/robot_song_song_2_9234.jpg)


![Đề cương đề tài nghiên cứu khoa học [chuẩn nhất/mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251117/duong297/135x160/26111763433948.jpg)













