m¹ch logic tæ hîp
I. §Æc ®iÓm c¬ b¶n cña m¹ch tæ hîp
Trong m¹ch sè, m¹ch tæ hîp lµ m¹ch mµ trÞ sè æn ®inh cña tÝn hiÖu ra ë
thêi ®iÓm bÊt kú chØ phô thuéc vµo tæ hîp c¸c gi¸ trÞ tÝn hiÖu ®Çu vµo ë
thêi ®iÓm tr-íc ®ã. Trong m¹ch tæ hîp, tr¹ng th¸i m¹ch ®iÖn tr-íc thêi
®iÓm xÐt – tr-íc khi cã tÝn hiÖu ®Çu vµo – kh«ng ¶nh h-ëng ®Õn tÝn
hiÖu ®Çu ra. §Æc ®iÓm cÊu tróc m¹ch tæ hîp lµ ®-îc cÊu tróc tõ c¸c
cæng logic.
II. Ph-¬ng ph¸p biÓu diÔn vµ ph©n tÝch chøc n¨ng logic
1. Ph-¬ng ph¸p biÓu diÔn chøc n¨ng logic
C¸c ph-¬ng ph¸p th-êng dïng ®Ó biÓu diÔn chøc n¨ng logic cña
m¹ch tæ hîp lµ hµm sè logic, b¶ng ch©n lý, s¬ ®å logic, b¶ng
Karnaugh, còng cã thÓ biÓu diÔn b»ng ®å thÞ thêi gian d¹ng sãng.
§èi víi vi m¹ch cì nhá (SSI) th-êng biÓu diÔn b»ng hµm logic. §èi víi
cì võa, th-êng biÓu diÔn b»ng b¶ng ch©n lý, hay lµ b¶ng chøc n¨ng.
B¶ng chøc n¨ng dïng h×nh thøc liÖt kª, víi møc logic cao (H) vµ møc
logic thÊp (L), ®Ó m« t¶ quan hÖ logic gi÷a tÝn hiÖu ®Çu ra víi tÝn hiÖu
®Çu vµo cña m¹ch ®iÖn ®ang xÐt.
ChØ cÇn thay gi¸ trÞ logic cho tr¹ng th¸i trong b¶ng chøc n¨ng th× ta cã
b¶ng ch©n lý t-¬ng øng.
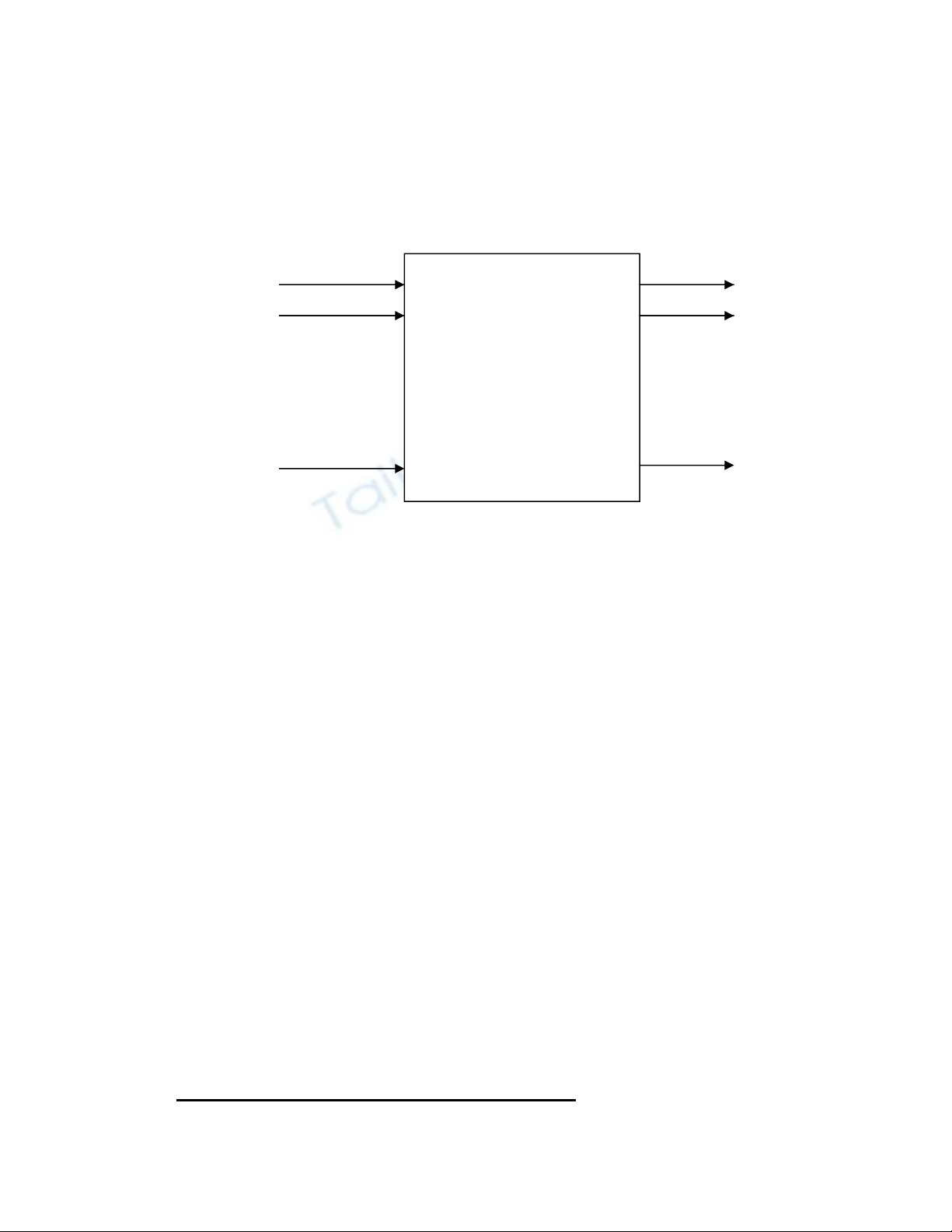
Nh- h×nh II.II.1 cho thÊy, th-êng cã nhiÒu tÝn hiÖu ®Çu vµo vµ nhiÒu tÝn
hiÖu ®Çu ra. Mét c¸ch tæng qu¸t, hµm logic cña tÝn hiÖu ®Çu ra cã thÓ
viÕt d-íi d¹ng:
Z1= f1(x1, x2, …, xn)
Z2= f2(x1, x2, …, xn)
…
Zm= fm(x1, x2, …, xn)
Còng cã thÓ viÕt d-íi d¹ng ®¹i l-îng vect¬ nh- sau:
Z= F(X)
2. Ph-¬ng ph¸p ph©n tÝch chøc n¨ng logic
Z
1
Z2
.
.
Zm
M¹ch tæ hîp
X
1
X2
.
.
Xn
H×nh II.II.1
-
S¬ ®å khèi m¹ch tæ hîp
C¸c b-íc ph©n tÝch, b¾t ®Çu tõ s¬ ®å m¹ch logic ®· cho, ®Ó cuèi
cïng t×m ra hµm logic hoÆc b¶ng ch©n lý.
+ ViÕt biÓu thøc: tuÇn tù tõ ®Çu vµo ®Õn ®Çu ra ( hoÆc còng cã
thÓ ng-îc l¹i), viÕt ra biÓu thøc hµm logic cña tÝn hiÖu ®Çu ra.
+ Rót gän: khi cÇn thiÕt th× rót gän ®Õn tèi thiÓu biÓu thøc ë trªn
b»ng ph-¬ng ph¸p ®¹i sè hay ph-¬ng ph¸p h×nh vÏ.
+ VÏ b¶ng sù thËt: khi cÇn thiÕt th× t×m ra b¶ng sù thËt b»ng c¸ch
tiÕn hµnh tÝnh to¸n c¸c gi¸ trÞ hµm logic tÝn hiÖu ®Çu ra t-¬ng øng víi
tæ hîp cã thÓ cña c¸c gi¸ trÞ tÝn hiÖu ®Çu vµo.
III. Ph-¬ng ph¸p thiÕt kÕ logic m¹ch tæ hîp
Ph-¬ng ph¸p thiÕt kÕ logic lµ c¸c b-íc c¬ b¶n t×m ra s¬ ®å
m¹ch ®iÖn logic tõ yªu cÇu vµ nhiÖm logic ®· cho.
VÊn ®Ò
logic thùc B¶ng
ch©n lý
B¶ng
Karnaugh Tèi thiÓu
ho¸
BiÓu thøc
tèi thiÓu S¬ ®å
logic
BiÓu thøc
logic
Tèi thiÓu
ho¸
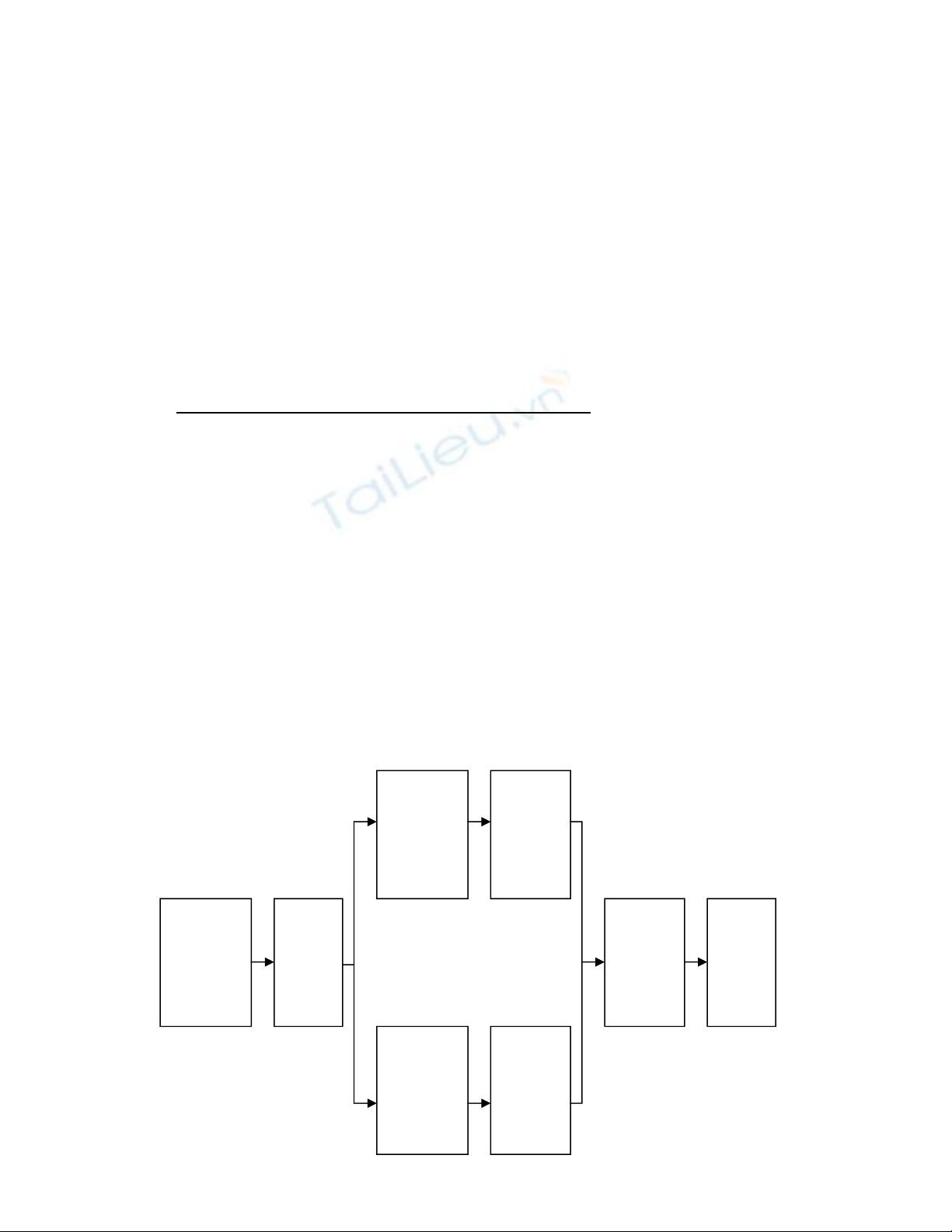
H×nh II.III.1
–
C¸c b-íc thiÕt kÕ m¹ch logic
tæ hîp
H×nh II.III.1 lµ qu¸ tr×nh thiÕt kÕ nãi chung cña m¹ch tæ hîp, trong ®ã
bao gåm bèn b-íc chÝnh:
1. Ph©n tÝch yªu cÇu:
Yªu cÇu nhiÖm vô cña vÊn ®Ò logic thùc cã thÓ lµ mét ®o¹n v¨n, còng
cã thÓ lµ bµi to¸n logic cô thÓ.
NhiÖm vô ph©n tÝch lµ x¸c ®Þnh c¸i nµo lµ biÕn sè ®Çu vµo, c¸i nµo lµ
hµm sè ®Çu ra vµ mèi quan hÖ logic gi÷a chóng víi nhau.
Muèn ph©n tÝch ®óng th× ph¶i t×m hiÓu xem xÐt mét c¸ch s©u s¾c yªu
cÇu thiÕt kÕ, ®ã lµ mét viÖc khã nh-ng quan träng trong vÊn ®Ò thiÕt kÕ.
2. VÏ b¶ng ch©n lý:
Nãi chung, ®Çu tiªn chóng ta liÖt kª thµnh b¶ng vÒ quan hÖ t-¬ng øng
nhau gi÷a tr¹ng th¸i tÝn hiÖu ®Çu vµo víi tr¹ng th¸i hµm sè ®Çu ra. §ã
lµ b¶ng kª yªu cÇu chøc n¨ng logic. gäi t¾t lµ b¶ng chøc n¨ng.
TiÕp theo, ta thay gi¸ trÞ logic cho tr¹ng th¸i, tøc lµ dïng c¸c sè 0 vµ 1
biÓu diÔn c¸c tr¹ng th¸i t-¬ng øng cña ®Çu vµo vµ ®Çu ra. KÕt qu¶, ta
cã b¶ng gi¸ trÞ thøc logic, gäi t¾t lµ b¶ng ch©n lý. §ã chÝnh lµ h×nh thøc
®¹i sè cña yªu cÇu thiÕt kÕ.
CÊn l-u ý r»ng tõ mét b¶ng chøc n¨ng cã thÓ ®-îc b¶ng sù thËt kh¸c
nhau nÕu thay gi¸ trÞ logic kh¸c nhau (tøc lµ quan hÖ logic gi÷a ®Çu ra
víi ®Çu vµo còng phô thuéc viÖc thay gi¸ trÞ).
3. TiÕn hµnh tèi thiÓu ho¸:
NÕu biÕn sè Ýt (d-íi 6 biÕn), th× th-ên dïng ph-¬ng ph¸p b¶ng
Karnaugh. Cßn nÕu biÕn sè t-¬ng ®èi nhiÒu th× dïng ph-¬ng ph¸p ®¹i
sè.
Ph-¬ng ph¸p Karnaugh:
ViÖc s¾p xÕp c¸c biÕn trªn bng mintec sao cho c¸c « ®øng c¹nh
nhau ®-îc biÓu diÔn b»ng bé gi¸ trÞ chØ c¸ch nhau 1 bit. C¬ së cña
ph-¬ng ph¸p Karnaugh dùa trªn tÝnh chÊt nuèt cña hµm sè logic, nghÜa
lµ:
A. B + A. B = A( B + B ) = A. 1 = A