M t s d ng toán tính đ oộ ố ạ ạ hàm
D ng 1:ạ Tính đ o hàm c a hàm s t i m t đi mạ ủ ố ạ ộ ể
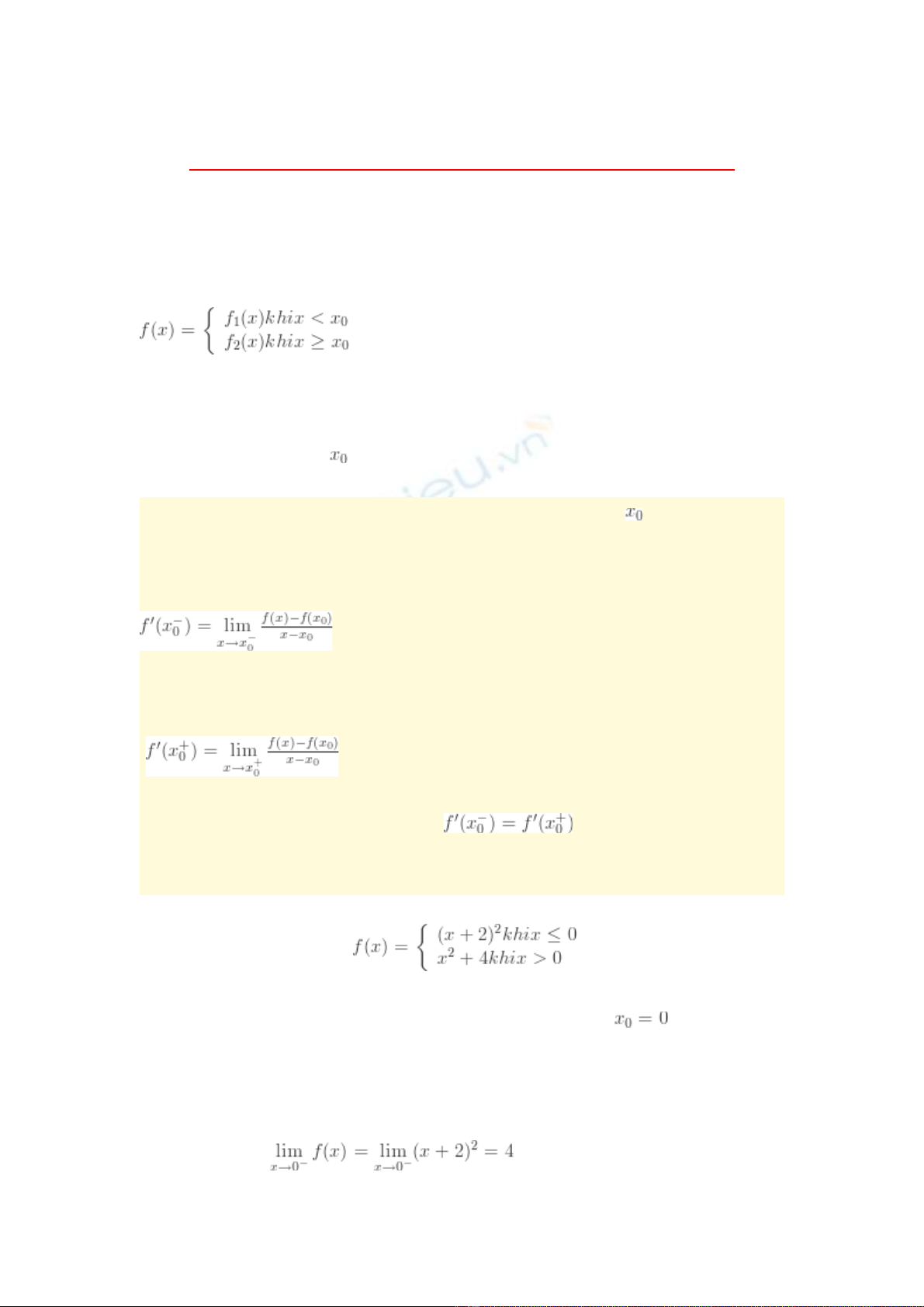
Cho hàm s :ố
Tính đ oạ hàm ho c xác đ nh giá tr c a tham s đ hàm s cóặ ị ị ủ ố ể ố
đ o hàm t i đi mạ ạ ể , ta th c hi n các b c sau:ự ệ ướ
B c 1:ướ Xét tính liên t c c a hàm s t i đi mụ ủ ố ạ ể
B c 2:ướ Tính (Đ o hàm bên trái):ạ
B c 3:ướ Tính (Đ o hàm bên ph i):ạ ả
B c 4:ướ Đánh giá ho c gi iặ ả , t đó đ a ra k từ ư ế
lu n.ậ
Ví d :ụ Cho hàm s :ố
Tính đ o hàm c a hàm s t iạ ủ ố ạ
L i gi i:ờ ả
•Ta có :
Do đó:
V y hàm s liên t c t i x=0ậ ố ụ ạ
•Đ o hàm bên trái c a hàm sạ ủ ố t i đi mạ ể
=
•Đ o hàm bên ph iạ ả c a hàm sủ ố t i đi mạ ể
=
Nh n xét : ậ nên hàm s không có đ o hàmố ạ
t i x=0ạ
•K t lu n:ế ậ Hàm s có đ o hàm bên trái, bên ph i , nh ngố ạ ả ư
khong có đ o hàm t i x=0.ạ ạ
D ngạ 2: Tính đ o hàm c a hàm s trên m t kho ng ( dùngạ ủ ố ộ ả
đ nh nghĩa).ị
Đ tính đ o hàm c a hàm s :ể ạ ủ ố trên m tộ
kho ngả , b ng đ nh nghiã , ta th c hi n các b c sau:ằ ị ự ệ ướ
B c 1:ướ Gi sả ử là s gia c a đ i s t iố ủ ố ố ạ , tính
B c 2:ướ L p t s :ậ ỉ ố
B c 3:ướ Tìm
Chú ý : N u kho ngế ả b ng đo nằ ạ , ta th c hi n theo cácự ệ
b c sau:ướ
B c 1: Tính đ o hàm c a hàm sướ ạ ủ ố trên
kho ngả .
B cướ 2: Tính đ o hàm bên ph i c a hàm sạ ả ủ ố t iạ
đi mể
= =
B cướ 3: Tính đ o hàm bên trái c a hàm sạ ủ ố t iạ
đi mể
Ví d :ụ Dùng đ nh nghĩa , tính đ o hàm c a hàm sị ạ ủ ố
sau:
L i gi i:ờ ả
Gi sả ử là s gia c a đ i s t iố ủ ố ố ạ , tính
= =
Do đó: = =
V y hàm s có đ o hàmậ ố ạ
Chú ý: Ta có th nói hàm sể ố có đ o hàmạ
trên các kho ngả và .