
1
S GIÁO D C VÀ ĐÀO T O THANH HÓAỞ Ụ Ạ
TR NG THPT NGUY N TRÃIƯỜ Ễ
SÁNG KI N KINH NGHI MẾ Ệ
RÈN LUY N KĨ NĂNG GI I M T S D NG BÀI T P Ệ Ả Ộ Ố Ạ Ậ
V HÌNH CHÓP DÀNH CHO H C SINH LUY N THI Ề Ọ Ệ
THPT QU C GIAỐ
Ng i th c hi n: Nguy n Th Bích Ph ngườ ự ệ ễ ị ượ
Ch c v : Giáo viênứ ụ
SKKN thu c lĩnh m c (môn): Toánộ ự
THANH HÓA NĂM 2016

M C L CỤ Ụ
A. M đuở ầ 01
I. Lý do ch n đ tàiọ ề 01
II. M c đích nghiên c uụ ứ 01
III. Đi t ng nghiên c uố ượ ứ 01
IV. Ph ng pháp nghiên c uươ ứ 01
B. N i dung sáng ki n kinh nghi mộ ế ệ 01
I. C s lí lu n c a sáng ki n kinh nghi mơ ở ậ ủ ế ệ 01
II. Th c tr ng v n đ tr c khi áp d ng sáng ki n kinh nghi mự ạ ấ ề ướ ụ ế ệ 02
III. Gi i pháp gi i quy t v n đả ả ế ấ ề 02
§1. C s khoa h cơ ở ọ 02
§2. M t s d ng toán minh h aộ ố ạ ọ 05
IV. Hi u qu c a sáng ki n kinh nghi mệ ả ủ ế ệ 19
C. K t lu n, ki n nghế ậ ế ị 20
D. Tài li u tham kh o, ph l c ệ ả ụ ụ
2

A. M ĐUỞ Ầ
I. Lý do ch n đ tàiọ ề
Quá trình gi ng d y và ôn luy n cho h c sinh d thi t t nghi p THPTả ạ ệ ọ ự ố ệ
Qu c Gia (tr c đây là thi Đi h c – Cao đng)… tôi nh n th y nhi u h c sinhố ướ ạ ọ ẳ ậ ấ ề ọ
g p khó khăn khi gi i bài t p hình h c không gian do kh năng t duy t ngặ ả ậ ọ ả ư ưở
t ng không gian c a h c sinh còn h n ch và có tâm lý s môn hình h c khôngượ ủ ọ ạ ế ợ ọ
gian. Trong khi đó, r t nhi u bài toán HHKG c a ch ng trình toán THPT có thấ ề ủ ươ ể
đc gi i quy t m t cách đn gi n h n r t nhi u khi v n d ng ph ng phápượ ả ế ộ ơ ả ơ ấ ề ậ ụ ươ
t a đ. Tuy nhiên, v n có nh ng bài toán gi i b ng ph ng pháp hình h c khôngọ ộ ẫ ữ ả ằ ươ ọ
gian thu n túy cho l i gi i đn gi n h n. Ngay c nh ng bài toán gi i đcầ ờ ả ơ ả ơ ả ữ ả ượ
b ng ph ng pháp t a đ thì bài toán có đn gi n hay không m t ph n phằ ươ ọ ộ ơ ả ộ ầ ụ
thu c vào cách ch n h tr c to đ. ộ ọ ệ ụ ạ ộ
Vì v y, trong khuôn kh bài vi t này tôi t p trung vào nh ng bài toán vậ ổ ế ậ ữ ề
hình chóp gi i đc b ng c hai ph ng pháp và khi áp d ng ph ng pháp t aả ượ ằ ả ươ ụ ươ ọ
đ vi c ch n h t a đ cũng đn gi n, d áp d ng giúp h c sinh gi i quy tộ ệ ọ ệ ọ ộ ơ ả ễ ụ ọ ả ế
đc m t s các bài toán hình h c không gian mà các em th ng g p trong các kìượ ộ ố ọ ườ ặ
thi cu i c p. ố ấ
II. M c đích nghiên c uụ ứ
Giúp h c sinh: Kh c ph c nh ng đi m y u khi gi i các bài toán hình h cọ ắ ụ ữ ể ế ả ọ
không gian nh : kh năng v hình không gian, kh năng t duy h n ch …Cóư ả ẽ ả ư ạ ế
cách nhìn t ng quát các bài toán hình h c không gian. L a ch n đc cách gi iổ ọ ự ọ ượ ả
thích h p nh t khi đng tr c m t bài toán. Xóa b tâm lý “s ” môn hình h cợ ấ ứ ướ ộ ỏ ợ ọ
không gian, gây h ng thú h c t p cho h c sinh. Có cách nhìn đa chi u v m tứ ọ ậ ọ ề ề ộ
v n đ trong cu c s ng.ấ ề ộ ố
III. Đi t ng nghiên c uố ượ ứ
Ph ng pháp gi i toán hình h c không gian: Ph ng pháp hình h c thu nươ ả ọ ươ ọ ầ
túy và ph ng pháp t a đ. M t s d ng toán v hình chóp có th v n d ngươ ọ ộ ộ ố ạ ề ể ậ ụ
3

ph ng pháp t a đ đ gi i toán. ươ ọ ộ ể ả u, nh c đi m c a m i ph ng phápƯ ượ ể ủ ỗ ươ
gi i toán.ả
IV. Ph ng pháp nghiên c uươ ứ
Ph ng pháp đi u tra kh o sát th c t , thu th p thông tin.ươ ề ả ự ế ậ
B. N I DUNG Ộ
I. C s lý lu n c a sáng ki n kinh nghi mơ ở ậ ủ ế ệ
Các bài toán thi vào Đi h c – Cao đng tr c đây và hi n nay khi các emạ ọ ẳ ướ ệ
đang ôn luy n đ b c vào kì thi THPT Qu c Gia đu đa đn d ng c a m tệ ể ướ ố ề ư ế ạ ủ ộ
bài toán HHKG ch không ph i d ng c a m t bài hình h c gi i tích không gian.ứ ả ạ ủ ộ ọ ả
Ph ng pháp hình h c không gian thu n túy, h c sinh c n s d ng thànhươ ọ ầ ọ ầ ử ụ
th o ki n th c HHKG đ v n d ng vào bài gi i (đi u này không ph i m i h cạ ế ứ ể ậ ụ ả ề ả ọ ọ
sinh đu nhìn ra). M t khác, vi c v hình không gian đúng, đp và khai thác t tề ặ ệ ẽ ẹ ố
hình v giúp r t nhi u cho vi c trình bày l i gi i m t bài toán HHKG nh ng khẽ ấ ề ệ ờ ả ộ ư ả
năng v hình c a ph n đông h c sinh r t y u. Ph ng pháp t a đ áp d ng vàoẽ ủ ầ ọ ấ ế ươ ọ ộ ụ
m t s d ng toán có th kh c ph c đc nh ng h n ch này. Tuy nhiên, khôngộ ố ạ ể ắ ụ ượ ữ ạ ế
ph i bài toán nào cũng áp d ng đc ph ng pháp t a đ đ gi i và cho l i gi iả ụ ượ ươ ọ ộ ể ả ờ ả
đn gi n.ơ ả
Nhìn chung hai ph ng pháp gi i toán, m i ph ng pháp đu có u đi mươ ả ỗ ươ ề ư ể
và nh c đi m cho nên vi c giúp h c sinh l a ch n ph ng pháp thích h p khiượ ể ệ ọ ự ọ ươ ợ
đng tr c m t bài toán hình h c không gian, giúp các em xác đnh đc h ngứ ướ ộ ọ ị ượ ướ
gi i toán, xây d ng ni m tin vào b n thân, t o h ng thú h c t p, xóa b tâm lýả ự ề ả ạ ứ ọ ậ ỏ
“s ” môn hình h c không gian là r t c n thi t.ợ ọ ấ ầ ế
II. Th c tr ng v n đ tr c khi áp d ng sáng ki n kinh nghi mự ạ ấ ề ướ ụ ế ệ
Ch ng trình toán THPT, h c sinh h c hình h c không gian v i hai n iươ ọ ọ ọ ớ ộ
dung tách r i nhau: Hình h c không gian thu n túy (h c l p 11 và h c k 1 c aờ ọ ầ ọ ở ớ ọ ỳ ủ
l p 12), ph ng pháp t a đ trong không gian (h c h c k 2 c a l p 12).ớ ươ ọ ộ ọ ở ọ ỳ ủ ớ
Ph n l n, h c sinh cho r ng hai n i dung này không liên quan v i nhau,ầ ớ ọ ằ ộ ớ
nghĩa là đ bài cho d i d ng HHKG thông th ng thì ph i gi i b ng HHKG.ề ướ ạ ườ ả ả ằ
H c sinh không th y m i liên h gi a hai n i dung này v i nhau: không bi tọ ấ ố ệ ữ ộ ớ ế
chuy n đi n i dung mô t hình h c không gian sang bi u th c gi i tích.ể ổ ộ ả ọ ể ứ ả
Phân ph i ch ng trình không có th i l ng cho h c sinh luy n t p, v nố ươ ờ ượ ọ ệ ậ ậ
d ng ph ng pháp t a đ gi i các bài toán HHKG mà các em đã bi t gi i tr cụ ươ ọ ộ ả ế ả ướ
đó.
Ki n th c, k năng, t duy toán c a h c sinh còn y u,kh năng t duyế ứ ỹ ư ủ ọ ế ả ư
t ng t ng hình không gian c a h c sinh còn h n ch và có tâm lý “s ” mônưở ượ ủ ọ ạ ế ợ
4
hình h c không gian nên nhi u h c sinh g n nh b qua bài hình h c không gianọ ề ọ ầ ư ỏ ọ
trong các đ thi mà các em g p.ề ặ
III. Gi i pháp đã s d ng đ gi i quy t v n đả ử ụ ể ả ế ấ ề
T th c tr ng trên, tôi ch n l c m t s d ng toán v hình chóp có th gi iừ ự ạ ọ ọ ộ ố ạ ề ể ả
đc b ng c hai ph ng pháp. ượ ằ ả ươ
M i bài toán đu trình bày c hai ph ng pháp gi i đ h c sinh có cáiỗ ề ả ươ ả ể ọ
nhìn t ng quát v bài toán hình h c không gian, th y đc u đi m, nh c đi mổ ề ọ ấ ượ ư ể ượ ể
c a m i ph ng pháp t đó hình thành kĩ năng đnh h ng gi i toán thích h p.ủ ỗ ươ ừ ị ướ ả ợ
Tuy nhiên, đ đ tài đt k t qu theo tôi giáo viên c n c ng c cho h cể ề ạ ế ả ầ ủ ố ọ
sinh m t s ki n th c sau:ộ ố ế ứ
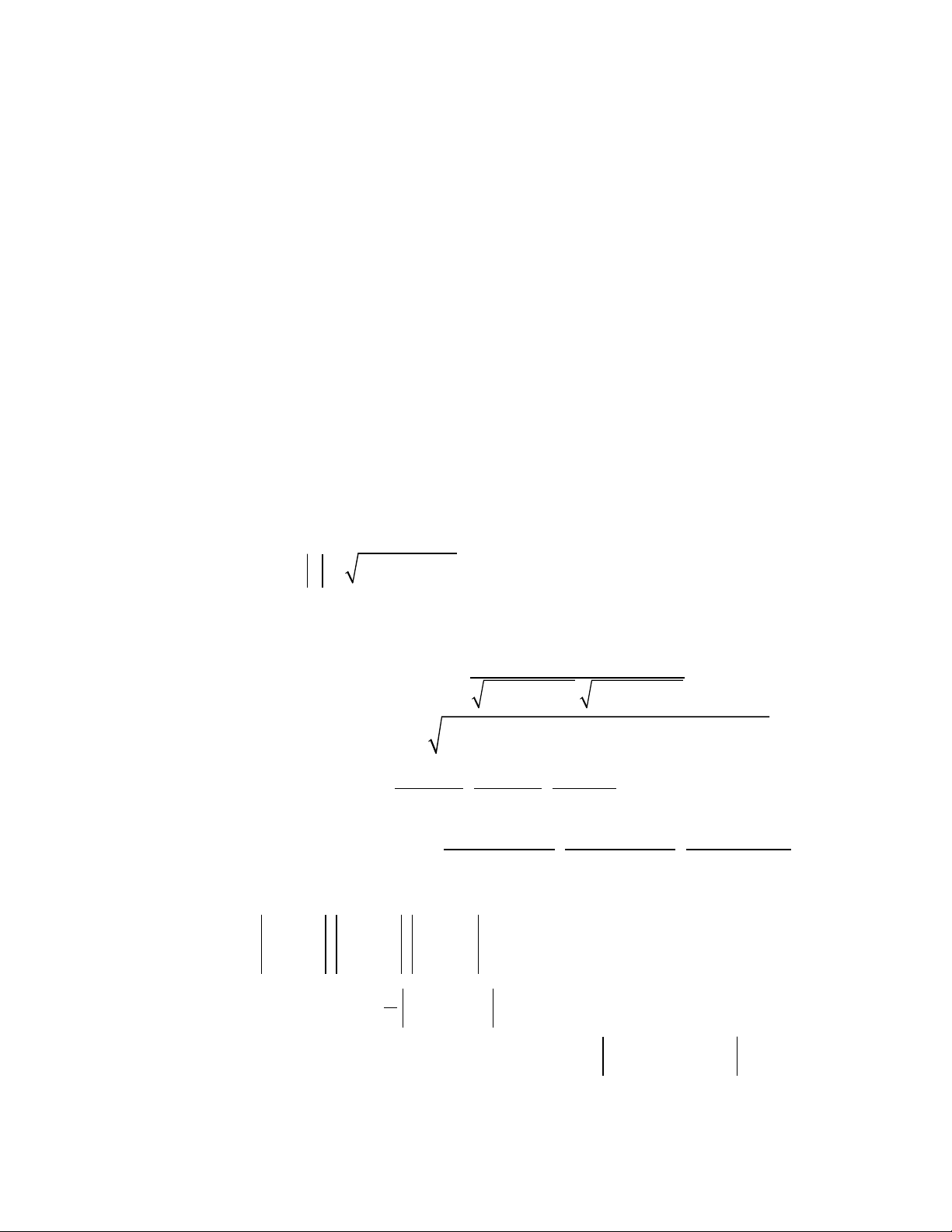
§ 1. C S KHOA H CƠ Ở Ọ
I. Ki n th c c b nế ứ ơ ả
T a đ véc t ọ ộ ơ
MN
uuuur
= (xN- xM ; yN - yM ; zN - zM )
Ta gi s ả ử
u
r
=(x1; y1; z1) ,
v
r
=(x2; y2; z2)
C ng , tr hai véc t : ộ ừ ơ
u
r
v
r
= ( x1
x2 ; y1
y2; z1
z2)
Nhân m t s v i m t véc t : k.ộ ố ớ ộ ơ
v
r
= (kx2; ky2; kz2) (k R)
Đ dài véc t : ộ ơ
2 2 2
2 2 2
v x y z= + +
r
Tích vô h ng c a hai véc t : ướ ủ ơ
u
r
.
v
r
= x1. x2 + y1.y2+ z1.z2
u
r
v
r
x1. x2 + y1.y2+ z1.z2 = 0
Góc gi a hai véc t : cos (ữ ơ
u
r
,
v
r
) =
1 2 1 2 1 2
2 2 2 2 2 2
1 1 1 2 2 2
x x y y z z
x y z x y z
. . .
.
+ +
+ + + +
Đ dài đo n th ng ộ ạ ẳ :
MN
=
( ) ( ) ( )
2 2 2
N M N M N M
x x y y z z− + − + −
M là trung đi m AB: ể
A B A B A B
x x y y z z
M ; ;
2 2 2
+ + +
� �
� �
� �
G là tr ng tâm c a ọ ủ ABC:
A B C A B C A B C
x x x y y y z z z
G ; ;
3 3 3
+ + + + + +
� �
� �
� �
Tích có h ng c a hai véc t : ướ ủ ơ
u
r
=(x1; y1; z1) và
v
r
=(x2; y2; z2) ký hi u là: ệ
w
ur
=
u v
� �
� �
r r
,
=
1 1 1 1 1 1
1 2 2 1 1 2 2 1 1 2 2 1
2 2 2 2 2 2
y z z x x y y z y z z x
y z z x x y
� �
= − − −
� �
� �
; ; ( . . ;z .x .x ;x .y .y )
Di n tích ệ
ABC
∆
là: S =
1AB AC
2
� �
� �
uuur uuur
,
Tính th tích hình h p: ABCD.A'B'C'D' là: ể ộ
V AB AD AA
� �
=� �
uuur uuur uuuur
, . '
5





















