
Sáng ki n kinh nghiế ệ
Đ tài :ề
D Y TOÁN (PH N HÌNH H C) L P 4Ạ Ầ Ọ Ớ
H và tên giáo viên : ọ
I. Đt v n đ ặ ấ ề :
Trong b n m ch ki n th c c b n c a Toán 4, m ch các y u t hình h cố ạ ế ứ ơ ả ủ ạ ế ố ọ
( YTHH ) không đóng vai trò tr ng tâm, c t lõi, th i l ng dành cho n i dung cácọ ố ờ ượ ộ
YTHH ch chi m kho ng 10% t ng th i l ng Toán 4. Nói nh v y, không cóỉ ế ả ổ ờ ượ ư ậ
nghĩa là m ch các YTHH không có vai trò trong ch ng trình, mà nó đc s p x pạ ươ ượ ắ ế
h p lí, đan xen v i m ch ki n th c s h c, đi l ng - đo đi l ng và gi i toánợ ớ ạ ế ứ ố ọ ạ ượ ạ ượ ả
làm n i rõ m ch ki n th c s h c và h tr h c t t các m ch ki n th c khác.ổ ạ ế ứ ố ọ ỗ ợ ọ ố ạ ế ứ
Vi c d y – h c các YTHH làm cho h c sinh có đc nh ng bi u t ng chínhệ ạ ọ ọ ượ ữ ể ượ
xác v m t s hình hình h c đn gi n và m t s đi l ng hình h c thông d ng ;ề ộ ố ọ ơ ả ộ ố ạ ượ ọ ụ
rèn cho h c sinh m t s kĩ năng th c hành nh bi t dùng êke đ v đng th ngọ ộ ố ự ư ế ể ẽ ườ ẳ
vuông góc, đng th ng song song, v chính xác hình ch nh t … ; phát tri n m tườ ẳ ẽ ữ ậ ể ộ
s năng l c trí tu nh phân tích, t ng h p, quan sát, so sánh, đi chi u, trí t ngố ự ệ ư ổ ợ ố ế ưở
t ng không gian đc phát tri n. Bên c nh đó, vi c d y – h c các YTHH làmượ ượ ể ạ ệ ạ ọ
tích lũy thêm nh ng hi u bi t c n thi t cho đi s ng sinh ho t và h c t p c a h cữ ể ế ầ ế ờ ố ạ ọ ậ ủ ọ
sinh. Ngoài ra các YTHH giúp h c sinh phát tri n đc nhi u năng l c trí tu ; rènọ ể ượ ề ự ệ
luy n đc nhi u đc tính và ph m ch t t t nh : c n th n, c n cù, chu đáo, khéoệ ượ ề ứ ẩ ấ ố ư ẩ ậ ầ
léo, a thích s chính xác, … Nh đó mà h c sinh có thêm ti n đ đ h c các mônư ự ờ ọ ề ề ể ọ
h c khác ti u h c, đ h c ti p môn toán b c trung h c c s và thích ng t tọ ở ể ọ ể ọ ế ở ậ ọ ơ ở ứ ố
h n v i môi tr ng t nhiên và xã h i xung quanh.ơ ớ ườ ự ộ
V i m c đích quan tr ng trên, tôi thi t nghĩ b n thân mình c n có s nhìnớ ụ ọ ế ả ầ ự
nh n m i v m ch ki n th c này. Đc bi t là c n có m t ph ng pháp d y h cậ ớ ề ạ ế ứ ặ ệ ầ ộ ươ ạ ọ
thích h p sao cho v a đt đc m c đích v a th c hi n đúng tinh th n c a vi cợ ừ ạ ượ ụ ừ ự ệ ầ ủ ệ
đi m i ph ng pháp d y h c.ổ ớ ươ ạ ọ
II. Nh ng bi n pháp đã th c hi nữ ệ ự ệ :
N i dung các YTHH trong ch ng trình Toán 4 bao g m :ộ ươ ồ
- Nh n bi t các góc : góc nh n, góc tù, góc b t.ậ ế ọ ẹ
- Nh n bi t hai đng th ng vuông góc v i nhauậ ế ườ ẳ ớ
- Bi t v hai đng th ng vuông góc, hai đng th ng song song, đngế ẽ ườ ẳ ườ ẳ ườ
cao c a m t tam giác.ủ ộ
- Nh n bi t hình bình hành, hình thoi, m t s đc đi m c a m i hình ; bi tậ ế ộ ố ặ ể ủ ỗ ế
cách tính chu vi và di n tích c a m i hình.ệ ủ ỗ
So v i các l p 1,2,3 thì s ti t v các YTHH l p 4 tăng lên nhi u. Song vớ ớ ố ế ề ở ớ ề ề
ph ng pháp gi ng d y thì ch y u v n là thông qua các ho t đng th c hành hìnhươ ả ạ ủ ế ẫ ạ ộ ự
h c ( đo, v , c t, ghép, g p, x p … hình ) đ giúp h c sinh n m đc m t s tínhọ ẽ ắ ấ ế ể ọ ắ ượ ộ ố
ch t đn gi n c a các hình và các quan h hình h c. N m đc đc đi m này, tôiấ ơ ả ủ ệ ọ ắ ượ ặ ể
đã c g ng t ch c các ho t đng th c hành là ch y u trong t t c các ti t gi ngố ắ ổ ứ ạ ộ ự ủ ế ấ ả ế ả
d y v các YTHH. C th :ạ ề ụ ể
1. Gi ng d y v gócả ạ ề :
l p 3, h c sinh đã đc làm quen v góc ( góc vuông, góc không vuông )Ở ớ ọ ượ ề
v i ớcách nh n bi t nh n bi t ậ ế ậ ế góc đó nh làư nh n d ng m t hình ( ậ ạ ộ góc g m ồđnh vàỉ
hai c nh, ạcó hình nh nh ả ư là góc t o b i kim ạ ở đngồ h , hai ồcái râu c a ăng ten ti vi...ủ
). Đn l p 4, ế ớ góc đđ cượ nh n bi t c th h nậ ế ụ ể ơ ( là các góc vuông, góc nh n, góc tù,ọ
góc b t ) v i các đc đi m c a m i góc so v i góc vuông ( góc nh n bé h n gócẹ ớ ặ ể ủ ỗ ớ ọ ơ
vuông, góc tù l n h n góc vuông, góc b t b ng hai góc vuông ). Tuy nhiên đ cóớ ơ ẹ ằ ể
bi u t ng v góc Ti u h c, h c sinh cũng ch y u d a vào quan sát t ng thể ượ ề ở ể ọ ọ ủ ế ự ổ ể
hình đ nh n bi t v góc.ể ậ ế ề
a. Gi i thi u góc nh n :ớ ệ ọ
* Ôn l i v cái ê ke :ạ ề
- GV cho HS l y cái ê ke, quan sátấ
- Cái ê ke hình gì ? ( …tam giác )
- Tam giác này có gì đc bi t ? ( …có 1 góc vuông )ặ ệ
- GV : Hôm nay chúng ta s s d ng ê ke đ ki m tra m t s góc.ẽ ử ụ ể ể ộ ố
- GV v lên b ng góc nh n AOBẽ ả ọ
- Hãy đc tên góc, tên đnh và các c nhọ ỉ ạ
c a góc nàyủ
- GV gi i thi u : Góc này là góc nh n.ớ ệ ọ
- Hãy dùng ê ke đ ki m tra đ l n c aể ể ộ ớ ủ
góc nh n AOB và cho bi t góc này nhọ ế ư
th nào so v i góc vuông.ế ớ
- GV nêu : Góc nh n bé h n góc vuông.ọ ơ
- Yêu c u HS v m t góc nh n ( HS sầ ẽ ộ ọ ử
d ng ê ke đ v góc nh h n góc vuôngụ ể ẽ ỏ ơ
)
- HS quan sát
- Góc AOB có đnh O, hai c nh OA vàỉ ạ
OB.
- HS nêu : Góc nh n AOBọ
- 1 HS lên b ng ki m tra, c l p theoả ể ả ớ
dõi, sau đó ki m tra góc AOB trong SGKể
-> góc nh n AOB bé h n gco1 vuông.ọ ơ
- 1 HS v b ng, HS c l p th c hànhẽ ả ả ớ ự
vào nháp.
b. T ng t nh th GV gi i thi u góc tù, góc b t. L u ý khi d y v góc b t,ươ ự ư ế ớ ệ ẹ ư ạ ề ẹ
GV v a v v a thao tác nh sau :ừ ẽ ừ ư
- GV v lên b ng góc b t COD -> yêuẽ ả ẹ
c u HS đc tên góc, tên đnh, tên cácầ ọ ỉ
c nh c a góc.ạ ủ
- GV tăng d n đ l n c a góc COD, đnầ ộ ớ ủ ế
khi hai c nh OC và OD c a góc COD “ạ ủ
th ng hàng” ( cùng n m trên m t đngẳ ằ ộ ườ
th ng ) v i nhau. Lúc đó góc COD đcẳ ớ ượ
g i là góc b t.ọ ẹ
- Góc COD có đnh là O, c nh OC vàỉ ạ
OD.
- Quan sát, theo dõi thao tác c a GVủ
c. Luy n t p :ệ ậ
- HS quan sát và đc tên đc các góc.ọ ượ
C
C
O
D
- HS bi t dùng ê ke đ ki m tra và phân lo i các góc cho tr c đ nh n raế ể ể ạ ướ ể ậ
tam giác ABC có ba góc nh n, tam giác DEG có m t góc vuông và tam giác MNPọ ộ
có m t góc tù.ộ
- Cho HS liên h trong th c t v các góc đã h c. Ví d :ệ ự ế ề ọ ụ
+ Góc nh n : m i ê ke đu có hai góc nh n, ch V in hoa,…ọ ỗ ề ọ ữ
+ Góc tù : hai cánh c a cái qu t tr n, d u mũ trong ch ô, â, …ủ ạ ầ ấ ữ
Ho c GV cũng có th liên h c ng c b ng cách cho HS s d ng 2 que tính x pặ ể ệ ủ ố ằ ử ụ ế
góc nh n r i m r ng góc đó ( b ng cách quay m t que ) đ đc l n l t gócọ ồ ở ộ ằ ộ ể ượ ầ ượ
vuông, góc tù, góc b t.ẹ
2. Gi ng d y v đng th ng vuông góc và đng th ng song songả ạ ề ườ ẳ ườ ẳ :
Ti p theo vi c h c v đng th ng, HS l p 4 đc làm quen v i hai quan hế ệ ọ ề ườ ẳ ớ ượ ớ ệ
hình
h c h t s c quan tr ng là quan h vuông góc và quan h song song gi a các đngọ ế ứ ọ ệ ệ ữ ườ
th ng.ẳ
Bi u t ng v hai đđ ng th ng vuông góc đc hình thành trên c s kéoể ượ ề ườ ẳ ượ ơ ở
dài mãi hai c nh liên ti p c a m t hình ch nh t. Hai đng th ng vuông góc v iạ ế ủ ộ ữ ậ ườ ẳ ớ
nhau t o thành b n góc vuông có đnh chung.ạ ố ỉ
đây hình ch nh t ch là công c đ hình thành bi u t ng v đng th ngỞ ữ ậ ỉ ụ ể ể ượ ề ườ ẳ
vuông góc và đng th ng song song. Do đó :ườ ẳ
- Sau khi kéo dài các c nh AB và AD ( c a hình ch nh t ABCD ) đ đc haiạ ủ ữ ậ ể ượ
đng th ng AB và AD vuông góc v i nhau thì giáo viên nên xóa b t các c nh BCườ ẳ ớ ớ ạ
và CD ( không c n thi t )đđ HS có th t p trung chú ý vào c nh AB và AD.ầ ế ể ể ậ ạ
T ng t nh v y, sau khi kéo dài các c nh AB và AD ( c a hình ch nh tươ ự ư ậ ạ ủ ữ ậ
ABCD ) đ đc hai đng th ng song song v i nhau thì giáo viên nên xóa b t cácể ượ ườ ẳ ớ ớ
c nh AB và CD, ch gi l i BC và AD mà thôi.ạ ỉ ữ ạ
- Trong quá trình gi ng d y, giáo viên c n quan tâm đn vi c yêu c u h c sinh :ả ạ ầ ế ệ ầ ọ
+ Ch ra đc các ví d v đng th ng song song vàđđ ng th ng vuôngỉ ượ ụ ề ườ ẳ ườ ẳ
góc trong th c t . Ch ng h n : hai thanhđđ ng ray xe l a song song v i nhau, haiự ế ẳ ạ ườ ử ớ
ch n song c a song song v i nhau; hai mép b ng liên ti p vuông góc v i nhau, c tấ ử ớ ả ế ớ ộ
c luôn vuông góc v i bóng n ng c a nó.ờ ớ ắ ủ
+ Nêu ra các ph n ví d v hai đng th ng không song song ( c t nhau ),ả ụ ề ườ ẳ ắ
hai đng th ng không vuông góc trong th c t ho c trong hình v đ h c sinh soườ ẳ ự ế ặ ẽ ể ọ
sánh, đi chi u.ố ế
A B
CD
A B
CD
- Cho h c sinh dùng th c t p v đđ ng th ng song song và đng th ngọ ướ ậ ẽ ườ ẳ ườ ẳ
vuông góc trên gi y k ô. ấ ẻ
- Bên c nh đó đ giúp h c sinh h c hình thành bi u t ng v đđ ng th ngạ ể ọ ọ ể ượ ề ườ ẳ
song song vàđđ ng th ng vuông góc đc chính xác, l p 4 ta còn d y h c sinhườ ẳ ượ ở ớ ạ ọ
cách dùng th c và ê ke đ v đng th ng đi qua m t đi m cho tr c và vuôngướ ể ẽ ườ ẳ ộ ể ướ
góc ( song song ) v i m t đng th ng cho tr c. Trong tr ng h p này, h c sinhớ ộ ườ ẳ ướ ườ ợ ọ
th ng t ra lúng túng trong vi c d ch chuy n ê ke khi đi m E n m các v tríườ ỏ ệ ị ể ể ằ ở ị
khác nhau. Vì v y thao tác m u c a giáo viên c n ch m, k t h p l i nói rõ ràng,ậ ẫ ủ ầ ậ ế ợ ờ
d t khoát đ h c sinh n m b t tr c khi các em th c hành. Có th h ng d n h cứ ể ọ ắ ắ ướ ự ể ướ ẫ ọ
sinh v đng th ng đi qua đi m E và vuông góc v i đng th ng AB theo cácẽ ườ ẳ ể ớ ườ ẳ
b c sau :ướ
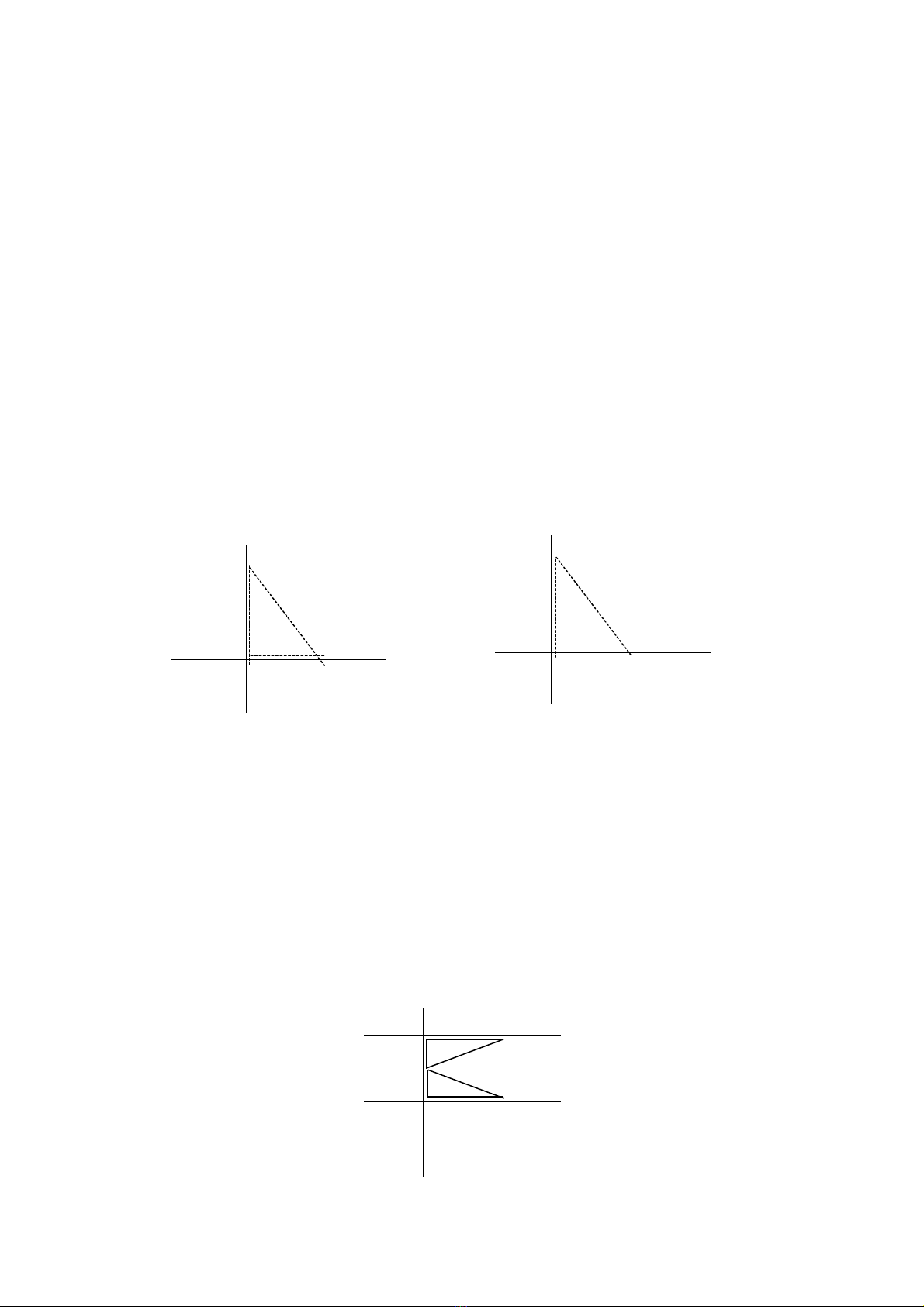
+ Đt m t c nh góc vuông c a ê ke trùng v i đng th ng AB.ặ ộ ạ ủ ớ ườ ẳ
+ Tr t ê ke theo đng th ng AB sao cho c nh th hai c a ê ke g p đi mượ ườ ẳ ạ ứ ủ ặ ể
E.
+ V ch đng th ng tạ ườ ẳ heo cạnh thứ hai của ê ke để được đường thẳng CD
đi qua điểm E và vuông góc với AB.
Đi m E n m trên đng th ng AB.ể ằ ườ ẳ Đi m E n m ngoài đng th ng AB.ể ằ ườ ẳ
Còn v i bài th c hành v hai đng th ng song song, giáo viên có th h ngớ ự ẽ ườ ẳ ể ướ
d n h c sinh nh sau :ẫ ọ ư
+ V đng th ng CD đi qua đi m E và vuông góc v i đng th ng AB.ẽ ườ ẳ ể ớ ườ ẳ
+ V đng th ng MN đi qua đi m E và vuông góc v i đng th ng CD.ẽ ườ ẳ ể ớ ườ ẳ
Tuy nhiên đ đt đc yêu c u c a ti t d y, khi h ng d n h c sinh vể ạ ượ ầ ủ ế ạ ướ ẫ ọ ẽ
hình, giáo viên c n chú ý :ầ
A B
C
D
E
C
A
E
DB
C D
E
A B
N
M

- Yêu c u h c sinh chu n b đy đ các d ng c nh : ê ke, th c. Bút, chì,ầ ọ ẩ ị ầ ủ ụ ụ ư ướ
gi y, t y.ấ ẩ
- T ch c cho h c sinh làm vi c theo các b c :ổ ứ ọ ệ ướ
+ Giao nhi m v .ệ ụ
+ H ng d n các thao tác, làm m u đ h c sinh quan sát.ướ ẫ ẫ ể ọ
+ L n l t cho h c sinh t tay th c hi n t ng b c. Giáo viên đi sát, đônầ ượ ọ ự ự ệ ừ ướ
đc, u n n n, giúp đ…ố ố ắ ỡ
+ Nh n xét.ậ
- Nên đt các đng th ng ặ ườ ẳ đã cho theo nh ng ph ng khác nhau. Tránh tìnhữ ươ
tr ng lúc nào cũng cho tr c m t đng th ng n m ngang.ạ ướ ộ ườ ẳ ằ
- Nh c nh h c sinh gi gìn c n th n d ng c th c hành.ắ ở ọ ữ ẩ ậ ụ ụ ự
- B n thân giáo viên cũng ph i h t s c m u m c và c n th n trong các thao tácả ả ế ứ ẫ ự ẩ ậ
s d ng th c và ê ke đ v hình trên b ng l p.ử ụ ướ ể ẽ ả ớ
Trên c s n m và th c hành t t vi c d ng hai đng th ng vuông góc ( songơ ở ắ ự ố ệ ự ườ ẳ
song ) thì h c sinh d dàng h c t t bài : Th c hành v hình vuông ; th c hành vọ ễ ọ ố ự ẽ ự ẽ
hình ch nh t.ữ ậ
3. Gi ng d y v hình bình hành và hình thoiả ạ ề :
Khái ni m hình bình hành, hình thoi đc gi i thi u, b sung giúp h c sinhệ ượ ớ ệ ổ ọ
bi t m t “h th ng” các hình t giác th ng g p trong th c t nh : hình vuông,ế ộ ệ ố ứ ườ ặ ự ế ư
hình ch nh t, hình bình hành, hình thoi. Đ nh n bi t đc đi m c a hình bìnhữ ậ ể ậ ế ặ ể ủ
hành, hình thoi, giáo viên c n t ch c cho h c sinh quan sát và quan sát chúng cácầ ổ ứ ọ ở
kích th c, góc đ khác nhau v i m c đích giúp các em có bi u t ng ban đu vướ ộ ớ ụ ể ượ ầ ề
hình bình hành và hình thoi. Sau đó có th t ch c cho các em làm vi c cá nhânể ổ ứ ệ
ho c làm vi c theo nhóm b ng thao tác đo đ dài c a các c nh, trao đi, nh n xétặ ệ ằ ộ ủ ạ ổ ậ
v chúng đ đi đn k t lu n : Hình bình hành có hai c p c nh đi di n song songề ể ế ế ậ ặ ạ ố ệ
và b ng nhau hay hình thoi có hai c p c nh đi di n song song và b n c nh b ngằ ặ ạ ố ệ ố ạ ằ
nhau. V i đc đi m c a hình bình hành, trong quá trình gi ng d y, giáo viên cũngớ ặ ể ủ ả ạ
nên đt v n đ : “ Hình ch nh t và hình vuông có đc g i là hình bình hànhặ ấ ề ữ ậ ượ ọ
không ? Vì sao ?”. Lí gi i đc đi u này tôi tin r ng là h c sinh đã n m bài r tả ượ ề ằ ọ ắ ấ
ch c. Bên c nh h th ng bài t p nh m giúp h c sinh n m đc đc đi m c aắ ạ ệ ố ậ ằ ọ ắ ượ ặ ể ủ
hình bình hành, hình thoi, tôi nghĩ ph n cu i bài giáo viên đa ra m t trò ch iở ầ ố ư ộ ơ
ho c thi t k m t bài t p v a mang tính gi i trí v a mang tính c ng c ki n th cặ ế ế ộ ậ ừ ả ừ ủ ố ế ứ
cao. Ví d : Ch dùng m t nhát kéo, em hãy c t các hình sau và ghép l i đ đcụ ỉ ộ ắ ạ ể ượ
hình bình hành.
H.1 H.2


























