
Trường THPT Vũ Duy Thanh Năm học 2013 - 2014
Sáng kiến kinh nghiệm 1 GV: Nguyễn Văn Long
A. ĐẶT VẤN ĐỀ
1. Lí do chọn đề tài
a. Cơ sở lý luận.
Hiện nay Bộ GD-ĐT đã áp dụng hình thức thi trắc nghiệm khách quan
trong kì thi tốt nghiệp THPT cũng như tuyển sinh Đại học, Cao đẳng đối với
nhiều môn học trong đó có môn vật lý. Hình thức thi trắc nghiệm khách quan
đòi hỏi học sinh phải có kiến thức rộng, xuyên suốt chương trình và có
kĩ năng làm bài, trả lời câu trắc nghiệm nhanh chóng. Bởi vậy, với mỗi
bài toán đề ra, người giáo viên không chỉ hướng dẫn học sinh hiểu bài mà
phải tìm cách giải nhanh nhất có thể.
Việc sử dụng mối liên hệ giữa dao động điều hòa và chuyển động tròn
đều để giải các bài tập dao động đã thỏa mãn được điều đó. Tuy nhiên,
không phải học sinh nào cũng nắm được thuần thục và nhanh nhạy công cụ
này do các em rất lúng túng khi dùng đường tròn lượng giác và khó tưởng
tượng được sự tương tự giữa hai loại chuyển động này. Trên thực tế, đã có
khá nhiều đề tài nghiên cứu xung quanh vấn đề này và đã thu được một số
kết quả nhất định. Tuy nhiên, hầu hết các tác giả chưa hoặc còn ít đề cập đến
bài toán vận dụng trực tiếp đường tròn lượng giác cho việc dùng hệ trục Oxv
(dao động cơ), hệ trục Ouu’ (trong điện xoay chiều) … Và hầu hết các đề tài
mới chỉ đề cập đến việc vận dụng mối liện hệ đó để giải quyết các bài toán
trong chương dao động cơ, còn ít đề cập đến các chương khác. Nên việc sử
dụng những kỹ năng giải nhanh các bài tập là rất cần thiết.
- Trong chương trình vật lí lớp 12 có 4 chương học liên quan đến các đại
lượng được biểu thị bằng các hàm số điều hoà (dạng hàm số cosin hay sin).
Đó là các chương:
Chương 1: Dao động cơ
Chương 2: Sóng âm và sóng cơ
Chương 3: Dòng điện xoay chiều
Chương 4: Dao động và sóng điện từ
Các đại lượng biểu thị bằng hàm số điều hoà thường gặp: li độ x, vận tốc v,
gia tốc a, lực kéo về
kv
F
???
, động năng, thế năng; phương trình truyền sóng,
cường độ dòng điện, hiệu điện thế, suất điện động cảm ứng, từ thông, điện
tích tụ điện, năng lượng điện trường của tụ điện, năng lượng từ trường của

Trường THPT Vũ Duy Thanh Năm học 2013 - 2014
Sáng kiến kinh nghiệm 2 GV: Nguyễn Văn Long
cuộn cảm.... Học sinh được học khá nhiều trong môn Toán về kiến thức các
hàm số lượng giác (hàm sin, cosin, tan, cot) ở lớp 11.
b. Cơ sở thực tiễn
- Lượng kiến thức, số câu hỏi trong các đề thi hiện nay liên quan đến hàm
điều hoà là tương đối nhiều. Số lượng các bài tập trong các đề thi tốt nghiệp
THPT, Cao đẳng và Đại học hàng năm liên quan đến các đại lượng biểu thị
theo hàm số điều hoà khá nhiều.
- Qua một số năm giảng dạy và ôn thi Đại học cho học sinh tôi thấy rằng
nếu giải theo cách truyền thống mất khá nhiều thời gian, cho nên rất cần có
những phương pháp giải nhanh cho các bài tập loại này góp phần đáp ứng yêu
cầu hình thức thi trắc nghiệm hiện nay. Học sinh đã được trang bị khá tốt kiến
thức các hàm số lượng giác, đặc biệt là đường tròn lượng giác trong môn toán.
Xuất phát từ thực tế đó tôi mạnh dạn nghiên cứu đề tài:
“SỬ DỤNG ĐƯỜNG TRÒN LƯỢNG GIÁC ĐỂ GIẢI NHANH MỘT
SỐ BÀI TOÁN DAO ĐỘNG ĐIỀU HÒA TRONG CHƯƠNG TRÌNH
VẬT LÍ 12 THPT”
2. Mục đích.
- Giúp học sinh hình thành kỹ năng giải nhanh một số bài toán vật lí bằng
cách sử dụng đường tròn lượng giác.
- Giúp học sinh nhận thức sâu sắc việc áp dụng kiến thức toán học phù hợp
để giải toán vật lí.
- Chỉ ra các mối quan hệ trực quan của các đại lượng vật lí, phương pháp,
thủ thuật sử dụng các công thức này để giải nhanh nhất, chính xác nhất các
bài tập.
- Thông qua đề tài rèn luyện, phát triển tư duy, tính sáng tạo của học sinh.
3. Đối tượng và phạm vi nghiên cứu.
- Các kiến thức của phần lượng giác trong toán học. Hàm số điều hoà, đồ
thị hàm điều hoà, đường tròn lượng giác.
- Kiến thức Vật lí, các đại lượng biến thiên điều hoà thuộc các chương
1,2,3,4 trong sách giáo khoa Vật lí 12.
- Học sinh: lớp 12A, 12E, 12G.
4. Phương pháp nghiên cứu.
Để hoàn thành đề tài này tôi chọn phương pháp nghiên cứu:
Trường THPT Vũ Duy Thanh Năm học 2013 - 2014
Sáng kiến kinh nghiệm 3 GV: Nguyễn Văn Long
- Phương pháp nghiên cứu tài liệu. Đọc các sách giáo khoa phổ thông sách
tham khảo phần: “Dao động điều hòa, sóng cơ học, sóng điện từ, dòng điện
xoay chiều…”
- Phương pháp thống kê. Chọn các bài có trong chương trình phổ thông, các
bài thường gặp trong các kì thi.
- Phương pháp phân tích và tổng hợp kinh nghiệm trong quá trình giảng dạy
và thực tế đời sống.
5. Phạm vi nghiên cứu.
Các bài tập có liên quan đến dao động điều hòa, sóng cơ học, dòng điện
xoay chiều, dao động điện từ.
B. GIẢI QUYẾT VẤN ĐỀ
I. Cơ sở lý thuyết áp dụng trong chuyên đề:
1. Kiến thức về đường tròn lượng giác
2. Mối liên hệ giữa dao động điều hoà và chuyển động tròn đều
- Chuyển động tròn đều là chuyển động có quỹ đạo là một đường tròn và
có độ lớn vận tốc không thay đổi.
- Các đại lượng đặc trưng trong chuyển động tròn đều: Bán kính R, chu kì
T, tần số f, tốc độ góc ω và tốc độ dài v.
- Công thức liên hệ: 2 1 2
2 ; ; ;
2
f T T f
T f
cos
sin
1
1
0
-1
-1
cos
sin
+
M
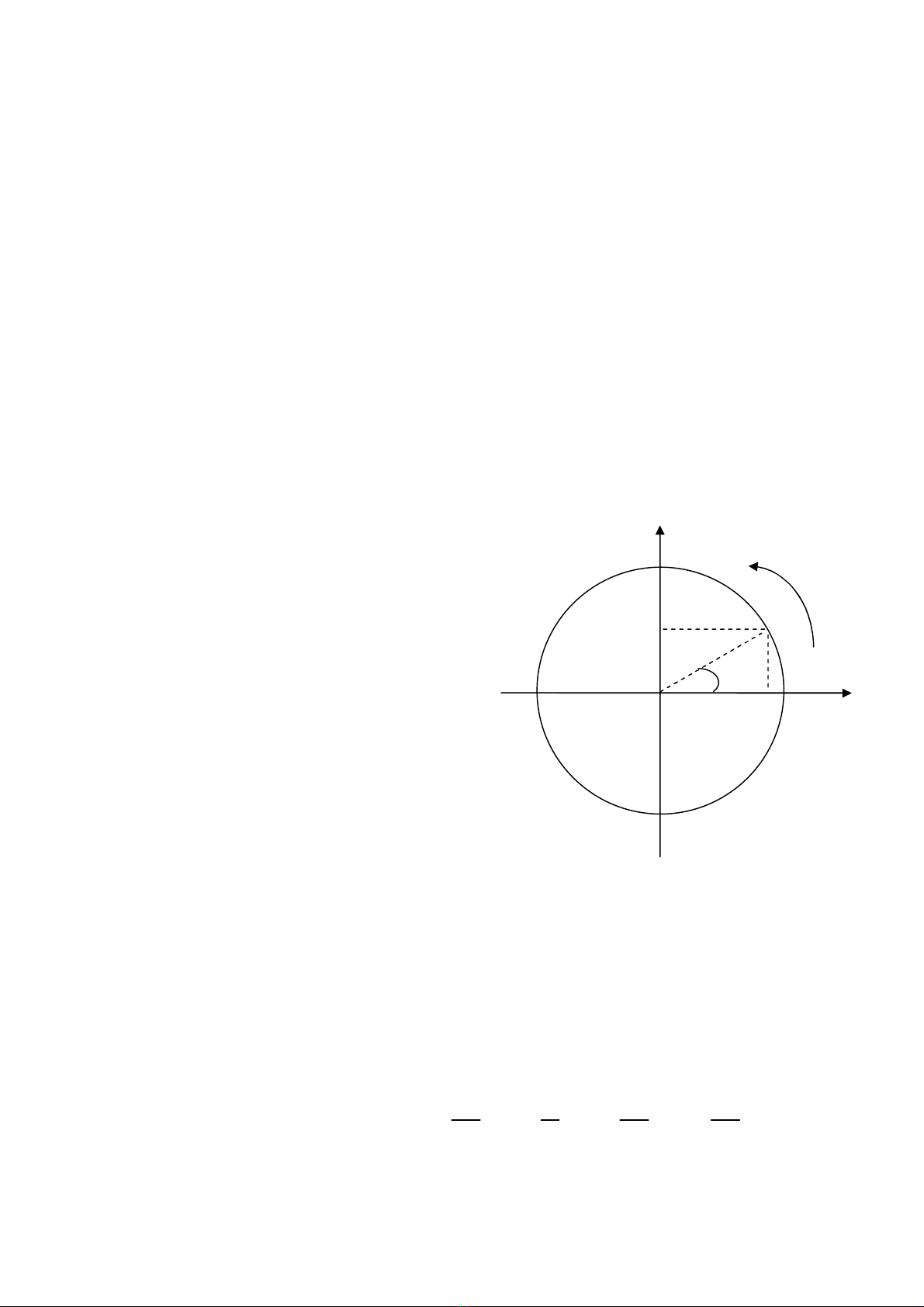
- Đường tròn lượng giác (vòng tròn
lượng giác): Là đường tròn tâm O, có
bán kính quy ước R = 1 đơn vị độ dài.
Trên đường tròn gắn hệ trục toạ độ Oxy,
trục hoành Ox biểu diễn giá trị hàm số
cosin, trên trục tung Oy biểu diễn giá trị
hàm số sin.
- Quy ước góc lượng giác tăng theo
chiều ngựơc kim đồng hồ; chiều dương
góc lượng giác ngược kim đồng hồ,
chiều âm góc lượng giác cùng chiều kim
đồng hồ.
Trường THPT Vũ Duy Thanh Năm học 2013 - 2014
Sáng kiến kinh nghiệm 4 GV: Nguyễn Văn Long
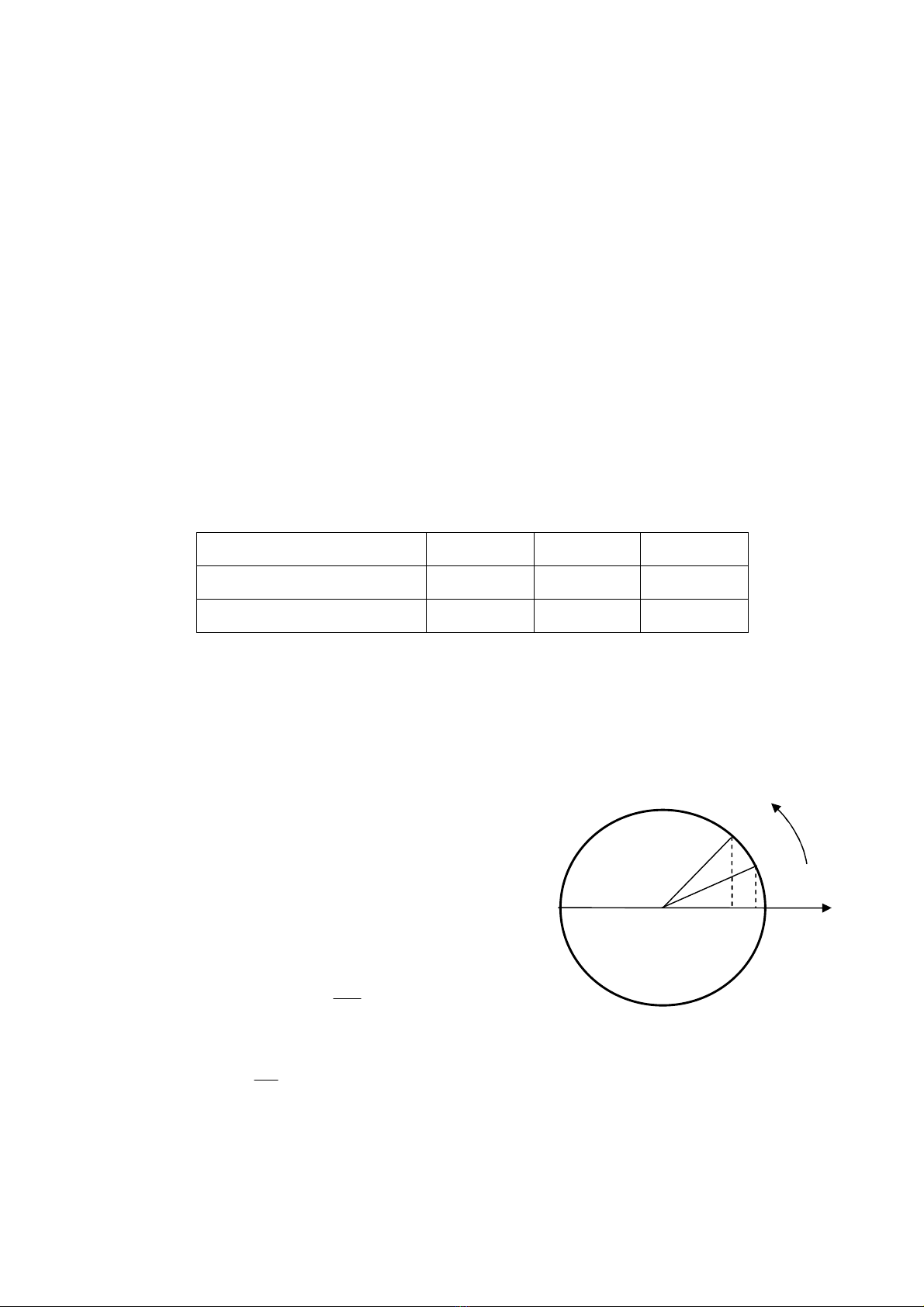
- Với một chất điểm chuyển động tròn đều, muốn xác định vị trí ta phải
chọn một trục Ox trên đường tròn làm mốc.
- Vị trí ban đầu của vật là M0, xác định bởi góc φ, với tốc độ góc ω, vào
thời điểm t vật đến vị trí M, có tọa độ xác định bởi góc α = ωt + φ (1).
- Lưu ý rằng trong dao động điều hòa tần số góc ω luôn dương, dẫn đến
góc quay ωt luôn dương nên vật luôn chuyển động theo chiều dương ngược
chiều kim đồng hồ.
- Ta có thể tạo mối liên hệ về hình thức của phương trình này với phương
trình của chuyển động thẳng biến đổi đều x=xo +vt. Việc này có tác dụng giúp
cho học sinh tiếp thu tốt khi phải tiếp xúc với một hình thức có phần lạ lẫm
của phương trình (1).
Các đại lượng tương ứng giữa chuyển động tròn đều
và chuyển động thẳng đều
Vị trí đầu Vị trí tại t Tốc độ
Chuyển động tròn đều φ α ω
Chuyển động thẳng đều
xo x v
Giả sử một điểm M chuyển động tròn đều trên đường tròn theo chiều
dương với tốc độ góc .
Vì hàm sin hay hàm cosin là hàm điều hoà, nên dao động của P là một
dao động điều hoà trên quỹ đạo P1P2 = 2A.
O
M
M0
x
P0
P
t
P2 P1
+
x
Đ
ặt bán kính quỹ
đ
ạo chuyển
đ
ộng
tròn đều của M là: R = OM = OM0 = A.
Gọi P là hình chiếu của điểm M lên
trục Ox trùng với một đường kính của
đường tròn và gốc O trùng với tâm của
đường tròn. Ta thấy P dao động trên Ox
quanh gốc toạ độ O. Vị trí ban đầu của P là
điểm P0 xác định: x0= 0
OP = Acosφ
vị trí P ở thời điểm t xác định bởi:
x = OP =Acos(ωt+φ)
Trường THPT Vũ Duy Thanh Năm học 2013 - 2014
Sáng kiến kinh nghiệm 5 GV: Nguyễn Văn Long
* Mở rộng.
Trong dao động điều hòa ta có các phương trình li độ, vận tốc, gia tốc như
sau:
cosx A t
sinv A t
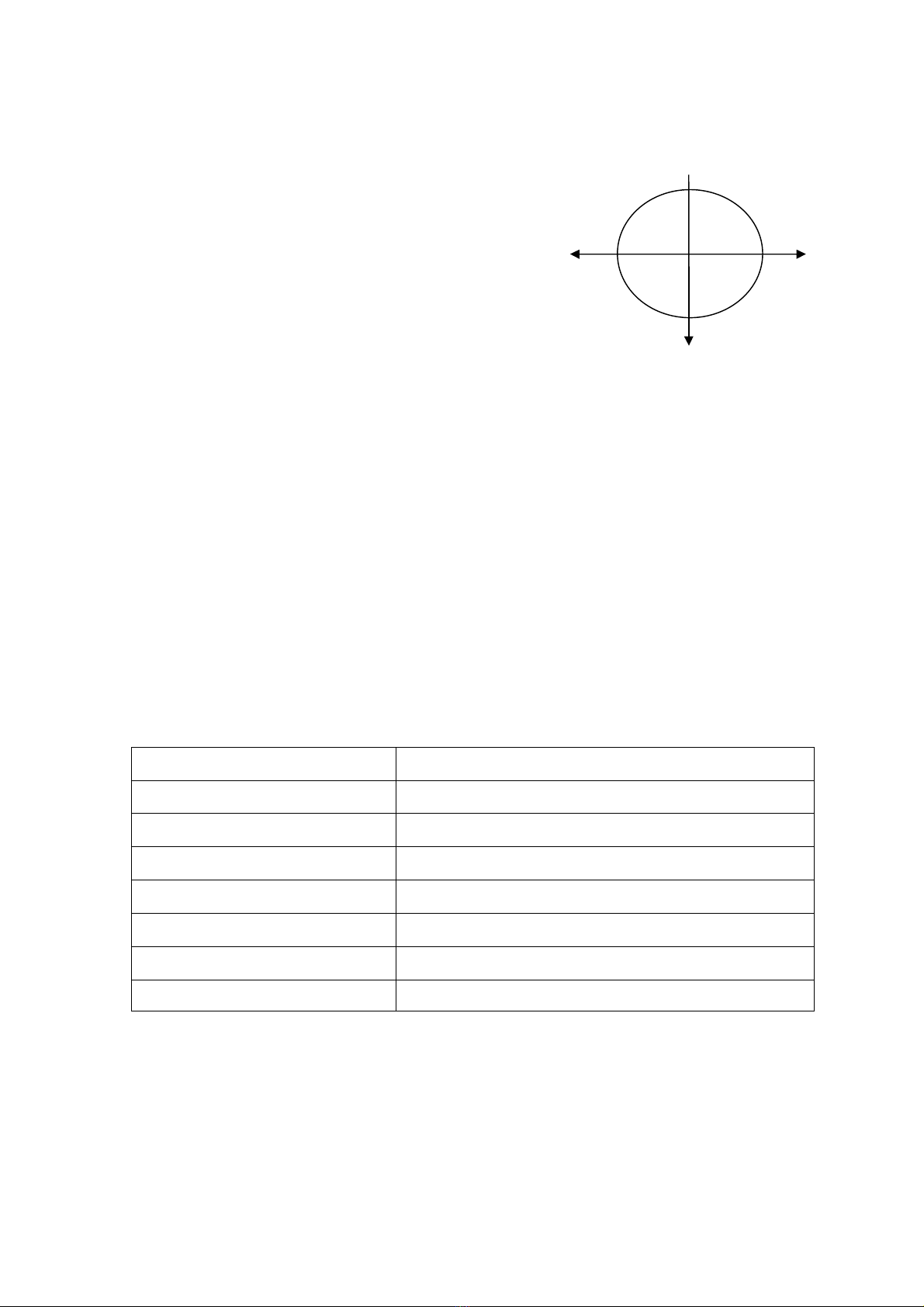
+ Li độ là hàm cosin nên được biểu diễn bằng
trục cosin có chiều dương hướng từ trái sang phải với biên độ là A
+ Vận tốc là hàm trừ sin nên được biểu diễn bằng trục ngược với trục
sin có chiều dương hướng từ trên xướng dưới với biên độ là A
+ Gia tốc là hàm trừ cosin nên được biểu diễn bằng trục ngược với trục
cosin có chiều dương hướng từ phải sang trái với biên độ là 2A
* Ý nghĩa
+ Khi ta biễu diễn một trong 3 đại lượng x, v, a ta có thể xác định được
ngay hai đại lượng còn lại một cách nhanh chóng.
+ Từ hình vẽ có thể nhận biết được nhiều thông tin bổ ích về tích chất
của một vật dao động điều hòa.
Sự tương ứng các đại lượng trong chuyển động tròn đều và
dao động điều hoà.
Chuyển động tròn đều Dao động điều hoà
Bán kính R Biên độ dao động A
Chu kỳ T Chu kỳ T
Tần số f Tần số f
Tốc độ góc ω Tần số góc ω
Góc ban đầu: φ Pha ban đầu: φ
Góc ở thời điểm t: ωt + φ Pha dao động ở thời điểm t: ωt + φ
Góc quét của bán kính: α = ωt Góc pha thay đổi trong khoảng thời gian t: α = ωt
3. Sự tích hợp giữa đường tròn lượng giác với kiến thức vật lí liên quan
- Xét một dao động điều hoà có: Phương trình dao động: x = Acos(ωt+φ)
Trong dao động ta quan tâm nhiều đến các vị trí đặc biệt ứng với các góc pha
đặc biệt. Có 9 vị trí tương ứng với các góc pha: 00, ±300, ±450, ±600, ±900,
±1200, ±1350, ±1500, 1800.
2cosa A t
x
v
0
2
A -
2
A
- A A
A
-
A
a






















