
1. PH N M ĐUẦ Ở Ầ
1.1. Lý do ch n đ tàiọ ề
Xu t phát t m c tiêu Giáo d c trong giai đo n hi n nay là ph i đào t o raấ ừ ụ ụ ạ ệ ả ạ
con ng i có trí tu phát tri n, giàu tính sáng t o và có tính nhân văn cao. Nh mườ ệ ể ạ ằ
đáp ng yêu c u m i trong nhu c u c a th i đi, vi c tri n khai ch ng trình giáoứ ầ ớ ầ ủ ờ ạ ệ ể ươ
d c ph thông, nh m th c hi n các m c tiêu, nhi m v c a Ngh Quy t s 29-ụ ổ ằ ự ệ ụ ệ ụ ủ ị ế ố
NQ/TW ngày 04/11/2013 Ban ch p hành Trung ng Đng ấ ươ ả v “Đi m i căn b n,ề ổ ớ ả
toàn di n giáo d c và đào t o, đáp ng yêu c u công nghi p hoá, hi n đi hoáệ ụ ạ ứ ầ ệ ệ ạ
trong đi u ki n kinh t th tr ng đnh h ng xã h i ch nghĩa và h i nh p qu cề ệ ế ị ườ ị ướ ộ ủ ộ ậ ố
t ” đã đc H i ngh l n th 8, Ban Ch p hành Trung ng (Khóa XI) thông qua.ế ượ ộ ị ầ ứ ấ ươ
Ngh quy t s 29 c a H i ngh BCH T l n th 8 (Khóa XI) là s k th a,ị ế ố ủ ộ ị Ư ầ ứ ự ế ừ
nâng cao c a Ngh quy t Trung ng 2 (Khóa 8). Theo đó, Trung ng Đng ti pủ ị ế ươ ươ ả ế
t c xác đnh phát tri n GD&ĐT là qu c sách hàng đu và trong xu th hi n nayụ ị ể ố ầ ế ệ
“Đi m i căn b n, toàn di n giáo d c và đào t o, đáp ng yêu c u công nghi pổ ớ ả ệ ụ ạ ứ ầ ệ
hoá, hi n đi hoá trong đi u ki n kinh t th tr ng đnh h ng xã h i ch nghĩaệ ạ ề ệ ế ị ườ ị ướ ộ ủ
và h i nh p qu c t ” nh m nâng cao ch t l ng ngu n nhân l c đc Đng taộ ậ ố ế ằ ấ ượ ồ ự ượ ả
xác đnh là m t trong ba đt phá chi n l c c a công cu c phát tri n đt n c.ị ộ ộ ế ượ ủ ộ ể ấ ướ
Quan đi m ch đo, m c tiêu, nhi m v và gi i pháp c a Ngh quy t s 29-ể ỉ ạ ụ ệ ụ ả ủ ị ế ố
NQ/TW c a BCH Trung ng đa ra đ t p trung lãnh, ch đo th c hi n 8 nhi mủ ươ ư ể ậ ỉ ạ ự ệ ệ
v và gi i pháp c b n theo đúng th c ti n c a s phát tri n kinh t xã h i trongụ ả ơ ả ự ễ ủ ự ể ế ộ
đó nhi m v gi i pháp th 2 là ti p t c đi m i m nh m và đng b các y u tệ ụ ả ứ ế ụ ổ ớ ạ ẽ ồ ộ ế ố
c b n c a giáo d c, đào t o theo h ng coi tr ng phát tri n ph m ch t, năng l cơ ả ủ ụ ạ ướ ọ ể ẩ ấ ự
c a ng i h c.ủ ườ ọ
Đó là m t cu c c i cách nh m nâng cao ch t l ng giáo d c toàn di n, phátộ ộ ả ằ ấ ượ ụ ệ
huy tính tích c c ch đng, sáng t o c a h c sinh, phù h p v i đc đi m c a t ngự ủ ộ ạ ủ ọ ợ ớ ặ ể ủ ừ
l p h c, môn h c, nh m tác đng đn tình c m, đem l i ni m vui h ng thú choớ ọ ọ ằ ộ ế ả ạ ề ứ
h c sinh, giúp các em tr thành nh ng con ng i phát tri n toàn di n (Đc, Trí,ọ ở ữ ườ ể ệ ứ
Th , M ...).ể ỹ
Toán h c là m t b môn c a khoa h c t nhiên đc ra đi và phát tri n r tọ ộ ộ ủ ọ ự ượ ờ ể ấ
s m. Ngay t khi ra đi Toán h c đã ph c v thi t th c cho đi s ng xã h i, h nớ ừ ờ ọ ụ ụ ế ự ờ ố ộ ơ
n a, Toán h c đc coi là c s c a nhi u ngành khoa h c, nó phát tri n t duy,ữ ọ ượ ơ ở ủ ề ọ ể ư
phát tri n năng l c trí tu và rèn luy n ph ng pháp suy lu n logic c a conể ự ệ ệ ươ ậ ủ
ng i.... Chính vì v y mà ngày nay Toán h c là môn h c chi m nhi u th i gianườ ậ ọ ọ ế ề ờ
nh t trong k ho ch đào t o c a nhà tr ng ph thông. Thông qua vi c h c t pấ ế ạ ạ ủ ườ ổ ệ ọ ậ
Toán h c, vi c h c sinh ngoài vi c n m v ng ki n th c còn bi t áp d ng vào th cọ ệ ọ ệ ắ ữ ế ứ ế ụ ự
ti n, vào lao đng s n xu t...ễ ộ ả ấ
Trong nhà tr ng ph thông, môn Toán nói chung và môn Hình h c nói riêngườ ổ ọ
gi m t v trí r t quan tr ng. Trong môn h c này, h c sinh đc h c nhi u ki nữ ộ ị ấ ọ ọ ọ ượ ọ ề ế
th c, nhi u ph ng pháp suy lu n, rèn luy n k năng tính toán, v hình. Ngoài raứ ề ươ ậ ệ ỹ ẽ
môn h c này còn góp ph n b i d ng cho h c sinh nh ng ph m ch t đo đc,ọ ầ ồ ưỡ ọ ữ ẩ ấ ạ ứ
tính linh ho t, đc l p, sáng t o.....ạ ộ ậ ạ
1

Nh ng do tính tr u t ng c a môn h c và là môn h c khó đi v i h c sinhư ừ ượ ủ ọ ọ ố ớ ọ
c p THCS. G p bài ch ng minh hình h c, h c sinh th ng lúng túng không bi tấ ặ ứ ọ ọ ườ ế
b t đu t đâu, v n d ng ki n th c nào đ gi i quy t v n đ. Do v y bài làm c aắ ầ ừ ậ ụ ế ứ ể ả ế ấ ề ậ ủ
nhi u h c sinh b sai, không hoàn ch nh ho c không tìm đc ph ng phápề ọ ị ỉ ặ ượ ươ
gi i...d n đn h c sinh ng i h c môn hình, trong khi tìm ph ng pháp gi i Toánả ẫ ế ọ ạ ọ ươ ả
hình h c ta g p m t s bài toán mà n u không v thêm đng ph thì có th bọ ặ ộ ố ế ẽ ườ ụ ể ế
t c. N u bi t v thêm đng ph thích h p t o ra s liên h gi a các y u t đãắ ế ế ẽ ườ ụ ợ ạ ự ệ ữ ế ố
cho thì vi c gi i toán tr nên thu n l i h n, d dàng h n. Th m chí có bài ph i vệ ả ở ậ ợ ơ ễ ơ ậ ả ẽ
thêm y u t ph thì m i tìm ra l i gi i.ế ố ụ ớ ờ ả
Tuy nhiên, trong sách giáo khoa ch trình bày m t s bài t p c b n v i th iỉ ộ ố ậ ơ ả ớ ờ
l ng ch a nhi u. V i các bài t p có liên quan đn v đng ph ph n l n h cượ ư ề ớ ậ ế ẽ ườ ụ ầ ớ ọ
sinh v n d ng ki n th c ch m ho c không bi t làm th nào đ v thêm đngậ ụ ế ứ ậ ặ ế ế ể ẽ ườ
ph đ gi i bài t p. Đi v i h c sinh khá gi i thì các d ng bài t p hình h c trongụ ể ả ậ ố ớ ọ ỏ ạ ậ ọ
SGK th ng ch a làm các em tho mãn vì tính ham h c, mu n khám phá tri th cườ ư ả ọ ố ứ
m i c a mình.ớ ủ
Hi n nay, trong kì thi h c sinh gi i Toán 7, các bài toán có v thêm y u tệ ọ ỏ ẽ ế ố
ph khá ph bi n. ụ ổ ế Tuy nhiên v thêm y u t ph nh th nào đ có l i cho vi cẽ ế ố ụ ư ế ể ợ ệ
gi i toán là đi u khó khăn và ph c t p. V y làm th nào đ h c sinh có th n mả ề ứ ạ ậ ế ể ọ ể ắ
đc m t s ph ng pháp v thêm y u t ph đ gi i các bài t p trong Hình h cượ ộ ố ươ ẽ ế ố ụ ể ả ậ ọ
7?
Xét trên th c t qua nh ng năm gi ng d y l p 7, đc bi t là trong công tácự ế ữ ả ạ ớ ặ ệ
b i d ng h c sinh gi i, tôi nh n th y nhu c u h c t p c a h c sinh, mu n đcồ ưỡ ọ ỏ ậ ấ ầ ọ ậ ủ ọ ố ượ
ti p thu các ki n th c b tr đ có th v n d ng vào vi c gi i các bài t p trongế ế ứ ổ ợ ể ể ậ ụ ệ ả ậ
các kì thi h c sinh gi i, các kì thi c p THCS, kì thi vào THPT ho c m t s tr ng,ọ ỏ ấ ặ ộ ố ườ
l p ch t l ng cao là r t c n thi t. Vì v y tôi m nh d n th c hi n sáng ki n kinhớ ấ ượ ấ ầ ế ậ ạ ạ ự ệ ế
nghi m: ệ“M t s Ph ng pháp v thêm y u t ph trong gi i toán hình h c l pộ ố ươ ẽ ế ố ụ ả ọ ớ
7”.
* Đi m m i c a Sáng ki nể ớ ủ ế
N i dung c a ộ ủ sáng ki n ếnày tr c đây đã có m t s ng i nghiên c u songướ ộ ố ườ ứ
n i dung còn chung chung, ch a đa ra các d ng bài c th .ộ ư ư ạ ụ ể Đi m m i trong ể ớ sáng
ki n ếnày, tôi t p trung trang b đy đ các d ng bài t p v n d ng m t s ph ngậ ị ầ ủ ạ ậ ậ ụ ộ ố ươ
pháp v thêm y u t ph . Đi v i m i d ng toán đa ra ph ng pháp gi i c thẽ ế ố ụ ố ớ ỗ ạ ư ươ ả ụ ể
và t p trung phân tích kĩ các ví d và bài t p áp d ng.ậ ụ ậ ụ Trong sáng ki nế này tôi đã
c g ng tìm ra m t s ví d v các ph ng pháp v thêm y u t ph , đa ra cácố ắ ộ ố ụ ề ươ ẽ ế ố ụ ư
d ng bài t p t ạ ậ ừ d đn khó, các bài t p nâng cao dành cho h c sinh khá gi i. Khiễ ế ậ ọ ỏ
g p d ng toán h c sinh d n m b t và ặ ạ ọ ễ ắ ắ giúp h c sinh ch đng đc cách gi i,ọ ủ ộ ượ ả
ch đng t duy tìm h ng gi i quy t cho các bài toán.ủ ộ ư ướ ả ế Sáng ki n ếth c hi n t iự ệ ạ
tr ng đang gi ng d y và áp d ng gi ng d y có hi u qu t t. N i dung v thêmườ ả ạ ụ ả ạ ệ ả ố ộ ẽ
y u t ph trong vi c gi i m t s bài toán th ng g p c p THCS có th nhânế ố ụ ệ ả ộ ố ườ ặ ở ấ ể
r ng áp d ng vào gi ng d y các đn v trên đa bàn. ộ ụ ả ạ ở ơ ị ị Mong r ng ằsáng ki n ếsẽ
đc các em h c sinh và đng nghi p đón nh n.ượ ọ ồ ệ ậ
2

1.2. Ph m vi áp d ng đ tài:ạ ụ ề
* Đi t ng nghiên c u:ố ượ ứ
- Nh đã trình bày trên nên trong sáng ki n này tôi ch nghiên c u trên haiư ở ế ỉ ứ
nhóm đi t ng c th sau:ố ượ ụ ể
1. Giáo viên d y toán THCSạ
2. H c sinh l p 7 THCS : bao g m 1 l p 7 v i t ng s 30 h c sinh và nhómọ ớ ồ ớ ớ ổ ố ọ
b i d ng h c sinh gi i toán 7.ồ ưỡ ọ ỏ
* Ph m vi nghiên c u:ạ ứ
- Trong sáng ki n này tôi ch nêu ra m t s “ph ng pháp v thêm y u tế ỉ ộ ố ươ ẽ ế ố
ph ” mà h c sinh ch a phát hi n ra trong quá trình ch ng minh các bài toán hìnhụ ọ ư ệ ứ
h c.ọ
- Phân tích m t s bài toán c th đ h c sinh nh n th y đc cách th c vộ ố ụ ể ể ọ ậ ấ ượ ứ ẽ
thêm y u t ph mà h c sinh không nh n ra d n t i không gi i đc các bài toànế ố ụ ọ ậ ẫ ớ ả ượ
ch ng minh hình h c, đc bi t là các bài toán khó.ứ ọ ặ ệ
- T đó đnh h ng cho h c sinh ph ng pháp gi i v thêm y u t ph khiừ ị ướ ọ ươ ả ẽ ế ố ụ
ch ng minh các bài toán hình h c.ứ ọ
* Ph m vi áp d ng ạ ụ sáng ki nế: Sáng ki n ếnày áp d ng cho h c sinh l p 7 vàụ ọ ớ
giáo viên d y Toán THCS n i b n thân đang công tác.ạ ơ ả
3

2. PH N N I DUNGẦ Ộ
2.1. Th c tr ng c a n i dung c n nghiên c uự ạ ủ ộ ầ ứ
Qua nhi u năm d y môn Hình h c l p 7, tôi nh n th y r ng, không cóề ạ ọ ớ ậ ấ ằ
ph ng pháp chung nh t choươ ấ vi c v thêm các y u t ph , mà là m t s sáng t oệ ẽ ế ố ụ ộ ự ạ
trong trong khi gi i toán, b i vì vi c v thêm các y u t ph c n đt đc m cả ở ệ ẽ ế ố ụ ầ ạ ượ ụ
đích là t o đi u ki n đ gi i đc bài toán m t cách ng n g n ch không ph i làạ ề ệ ể ả ượ ộ ắ ọ ứ ả
m t công vi c tu ti n. H n n a, vi c v thêm các y u t ph ph i tuân theo cácộ ệ ỳ ệ ơ ữ ệ ẽ ế ố ụ ả
phép d ng hình c b n và các bài toán d ng hình c b n, nhi u khi ng i giáoự ơ ả ự ơ ả ề ườ
viên đã tìm ra cách v thêm y u t ph nh ng không th gi i thích rõ cho h c sinhẽ ế ố ụ ư ể ả ọ
hi u đc vì sao l i ph i v nh v y, khi h c sinh h i giáo viên: T i sao cô (th y)ể ượ ạ ả ẽ ư ậ ọ ỏ ạ ầ
l i nghĩ ra đc cách v đng ph nh v y, ngoài cách v này còn có cách nàoạ ượ ẽ ườ ụ ư ậ ẽ
khác không? hay t i sao ch v thêm nh v y m i gi i đc bài toán? G p ph iạ ỉ ẽ ư ậ ớ ả ượ ặ ả
tình hu ng nh v y, qu th t ng i giáo viên cũng ph i r t v t v đ gi i thíchố ư ậ ả ậ ườ ả ấ ấ ả ể ả
mà có khi hi u qu cũng không cao, h c sinh không nghĩ đc cách làm khi g pệ ả ọ ượ ặ
bài toán t ng t vì các em ch a bi t các căn c cho vi c v thêm y u t ph . Tươ ự ư ế ứ ệ ẽ ế ố ụ ừ
th c t gi ng d y tôi th y r ng: đ gi i quy t v n đ này m t cách tri t đ, m tự ế ả ạ ấ ằ ể ả ế ấ ề ộ ệ ể ặ
khác l i nâng cao năng l c gi i toán và b i d ng kh năng t duy t ng quát choạ ự ả ồ ưỡ ả ư ổ
h c sinh, t t nh t ta nên trang b cho các em nh ng c s c a vi c v thêm đngọ ố ấ ị ữ ơ ở ủ ệ ẽ ườ
ph và m t s ph ng pháp th ng dùng khi v thêm y u t ph , cách nh n bi tụ ộ ố ươ ườ ẽ ế ố ụ ậ ế
m t bài toán hình h c c n ph i v thêm y u t ph , t đó khi các em ti p xúc v iộ ọ ầ ả ẽ ế ố ụ ừ ế ớ
m t bài toán, các em có th ch đng đc cách gi i, ch đng t duy tìm h ngộ ể ủ ộ ượ ả ủ ộ ư ướ
gi i quy t cho bài toán, nh v y hi u qu s cao h n.ả ế ư ậ ệ ả ẽ ơ
* S li u kh o sát tr c khi áp d ng đ tài:ố ệ ả ướ ụ ề
4
Tr c khi áp d ng đ tài tôi đã ti n hành kh o sát v i n i dung ki n th cướ ụ ề ế ả ớ ộ ế ứ
liên quan đn v thêm y u t ph trên 30 h c sinh. ế ẽ ế ố ụ ọ K t qu đt đc nh sau:ế ả ạ ượ ư
0 - < 2 2 - < 5 5 - < 6,5 6,5 - < 8 8 – 10
SL % SL % SL % SL % SL %
01 3,3 12 40,0 10 33,3 05 16,7 02 6,7
2.2. Các gi i phápả
2.2.1. C s lý lu n c a vi c v thêm y u t phơ ở ậ ủ ệ ẽ ế ố ụ
Vi c v thêm các y u t ph ph i tuân theo các phép d ng hình c b n vàệ ẽ ế ố ụ ả ự ơ ả
m t s bài toán d ng hình c b n. Sau đây là m t s bài toán d ng hình c b nộ ố ự ơ ả ộ ố ự ơ ả
trong ch ng trình THCS.ươ
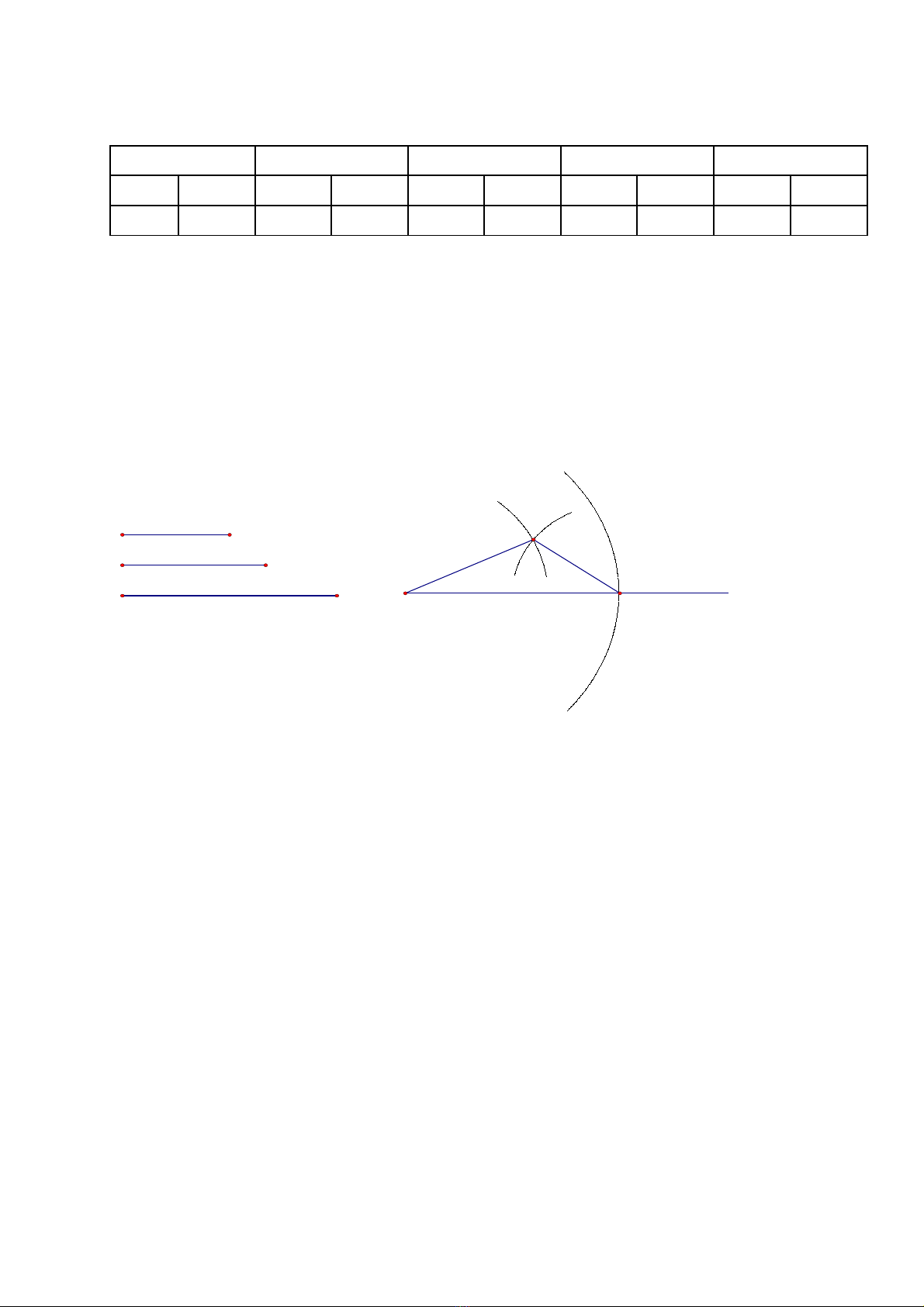
Bài toán 1: D ng m t tam giác bi t đ dài ba c nh c a nó là a; b; c.ự ộ ế ộ ạ ủ
c
b
a
c
b
a
x
C
A
B
Gi i:ả
* Cách d ng:ự
- D ng tia Ax.ự
- D ng đng tròn (A, c). G i B là giao đi m c a đng tròn (A, c) v i tiaự ườ ọ ể ủ ườ ớ
Ax.
- D ng đng tròn (A, b) và đng tròn (B, a), g i C là giao đi m c aự ườ ườ ọ ể ủ
chúng. Tam giác ABC là tam giác ph i d ng vì có AB = c; AC = b và BC = a.ả ự
Chú ý: N u hai đng tròn (A, b) và (B, a) không c t nhau thì không d ngế ườ ắ ự
đc tam giác ABC.ượ
Bài toán 2: D ng m t góc b ng góc cho tr c.ự ộ ằ ướ
Cách d ng: ự
G i ọ
ᄋ
xOy
là góc cho tr c. D ng đng tròn (O, r) c t Ox A và c t Oy ướ ự ườ ắ ở ắ ở
B ta đc ượ OAB.
D ng ựO’A’B’ = OAB ( c.c. c) nh bài toán 1, ta đc ư ượ
ᄋ
ᄋ
'O O=
.
5


























