
Rèn luyện kĩ năng vận dụng tính chất dãy tỉ số bằng nhau vào một số bài toán lớp 7
SÁNG KIẾN KINH NGHIỆM
“RÈN LUYỆN KĨ NĂNG VẬN DỤNG TÍNH CHẤT DÃY TỈ SỐ
BẰNG NHAU VÀO MỘT SỐ BÀI TOÁN LỚP 7 ”
A. ĐẶT VẤN ĐỀ
I .Lý do chọn đề tài:
Bộ môn toán ở cấp học THCS nhằm nâng cao dần kiến thức ,kĩ năng tư duy
toán học và vận dụng toán học vào thực tế. Vì vậy việc học tập bộ môn này đòi
hỏi sự rèn luyện, tư duy và cố gắng liên tục của mỗi học sinh. Để giúp các em
học tập đạt kết quả tốt. Giáo viên không chỉ nắm được kiến thức, mà điều cần
thiết là phải biết vận dụng các phương pháp giảng dạy một cách linh hoạt, truyền
thụ kiến thức cho học sinh dễ hiểu nhất đồng thời đổi mới phương pháp dạy học
theo định hướng phát triển năng lực học sinh. Xuất phát từ yêu cầu thực tế trong
quá trình giảng dạy toán 7 có nhiều dạng toán sử dụng tính chất dãy tỉ số bằng
nhau để giải một số dạng toán nhanh, chính xác. Vì vậy giáo viên phải có
phương pháp giải bài tập theo từng dạng và có hướng giải bài tập theo nhiều
cách khác nhau. Do vậy việc hướng dẫn các em có kĩ năng biến đổi để vận dụng
tính chất của dãy tỉ số bằng nhau vào các bài toán là rất cần thiết, từ đó
phát triển tư duy, đồng thời tạo hứng thú học tập của học sinh nên tôi đã tiến
hành học tập tích lũy kinh nghiệm trong quá trình giảng dạy và soạn ra đề tài.
II. MỤC ĐÍCH ,YÊU CẦU,NHIỆM VỤ CỦA ĐỀ TÀI
Thông qua đề tài “ Rèn luyện kĩ năng vận dụng tính chất dãy tỉ số bằng
nhau vào giải toán” nhằm giúp các em chủ động kiến thức,biết vận dụng kiến
thức đúng vào giải quyết những dạng bài tập, từ đó các em không còn phải lo
lắng, lúng túng và mắc phải những sai lầm khi bắt gặp dạng toán này. Bên cạnh
đó học sinh còn được rèn luyện :
- Kỹ năng phân tích một bài tập toán nói chung và từng dạng toán nói riêng
- Kỹ năng vận dụng kiến thức và biến đổi các bài tập về dạng dãy tỉ số bằng
nhau để áp dụng được công thức giải toán thuận lợi. Biết đưa các bài tập mang
nội dung thực tế khó giải quyết về các bài tập đơn giản ,dễ hiểu hơn. Giúp các
em nắm vững kiến thức vận dụng vào bài kiểm cho một tiết, bài kiểm tra học kì,
đặc biệt là kì thi học sinh giỏi.
III. ĐÔI TƯỢNG, PHẠM VI,THỜI GIAN THỰC HIỆN ĐỀ TÀI
-Đối tượng nghiên cứu của đề tài này là học sinh lớp 7A,7B tại trường THCS nơi
tôi công tác.
-Phạm vi: Kiến thức lớp 7, vận dụng cho cả các bài toán lớp 8; 9 THCS
-Thời gian nghiên cứu: Tôi vận dụng dạy vào những tiết học chính khóa, kết
hợp với 12 tiết vào những buổi bồi dưỡng nhu cầu của năm học 2019-2020

IV. PHƯƠNG PHÁP NGHIÊN CỨU:
- Phương pháp nghiên cứu tài liệu
- Phương pháp thu thập và sử lí số liệu.
- Phương pháp thực nghiệm: Giảng dạy, kiểm tra - đánh giá theo định hướng
phát triển năng lực, phẩm chất học sinh
B – QUÁ TRÌNH THỰC HIỆN ĐỀ TÀI.
I. KHẢO SÁT THỰC TẾ.
Trong quá trình dạy học tôi nhận thấy sự phát hiện ,tìm tòi ,suy luận để tìm ra
hướng giải một bài toán của các em còn rất yếu , nguyên nhân chủ yếu là do các
em chưa phân loại được các dạng bài tập và phương pháp giải đối với từng loai
và lúng túng khi gặp một dạng mới. Đối với bài toán áp dụng tính chất dãy tỷ số
bằng nhau lớp 7 là một trong những dạng toán mà hầu hết các em đều cảm thấy
bỡ ngỡ,còn hiểu lơ mơ về tính chất dãy tỷ số bằng nhau ,các em chưa biết áp
dụng tính chất dãy tỷ số bằng nhau như thế nào cho đúng và cần biến đổi dãy
tỷ số cho trước như thế nào để có thể áp dụng tính chất dãy tỷ số bằng nhau vào
bài toán cụ thể .Qua giảng dạy và lắng nghe thông tin phản hồi của các em kết
hợp với công tác dự giờ rút kinh nghiệm tôi đã phần nào rút ra nguyên nhân và
cách giải quyết để giúp cho học sinh nắm trắc tính chất dãy tỷ số bằng nhau từ
đó vận dụng làm một số dạng bài tập và có hướng giải đúng.
Sau khi học song tiết 11 bài tính chất dãy tỉ số bằng nhau chương I đại số lớp 7
tôi cho 36 học sinh lớp 7 làm bài kiểm tra khảo sát vào buổi chiều trước khi thực
hiện đề tài với nội dung ở phiếu số 1 (phần phụ lục). Tôi thấy kết quả làm bài
của học sinh còn thấp, còn mắc nhiều lỗi sai khi trình bày ,còn lúng túng trong
việc sử dụng tính chất dãy tỷ số bằng nhau,...Vì vậy để các em thực sự yêu thích
môn toán học nói chung và các bài toán vận dụng tính chất dãy tỉ số bằng nhau
nói riêng. Khi các em đã được trang bị đầy đủ kiến thức tôi cho học sinh củng cố
để nắm vững và hiểu thật sâu về tính chất tỉ lệ thức, dãy tỉ số bằng nhau từ đó
cho các em vận dụng làm một số dạng bài toán để tìm ra một định hướng, một
quy luật nào đó làm cơ sở cho việc chọn lời giải, có thể minh hoạ điều đó bằng
các dạng toán, bằng các bài toán từ đơn giản đến phức tạp.
* Các biện pháp thực hiện.
Giáo viên hệ thống hóa kiến thức cho học sinh
-Lựa chon bài tập phù hợp với từng đối tượng học sinh
-Hướng dẫn học sinh phân tích bài toán và từng bước giải quyết vấn đề
-Giao nhiệm vụ cho từng cá nhân,nhóm ,tổ và chỉ rõ thời gian hoàn thành nhiệm
vụ.
Rèn luyện kĩ năng vận dụng tính chất dãy tỉ số bằng nhau vào một số bài toán lớp 7
II. CÁC GIẢI PHÁP CỤ THỂ
Giải pháp 1:Củng cố và hệ thống lí thuyết về tỉ lệ thức, tính chất của tỉ lệ
thức ,dãy tỉ số bằng nhau
1.Lí thuyết cần nắm vững
1.1. Định nghĩa của tỉ lệ thức: Tỉ lệ thức là đẳng thức giữa hai tỉ số .
Ta còn viết: a : b = c : d.
Trong đó a và d là các ngoại tỉ; b và c là các trung tỉ
1.2. Tính chất của tỉ lệ thức:
a c
b d
=
Tính chất 1: Nếu
a c
b d
=
thì a.d = b.c
Tính chất 2: Nếu a.d = b.c với a, b, c, d ≠ 0 thì ta có các tỉ lệ thức:
a c
b d
=
;
a b
c d
=
;
d c
b a
=
;
d b
c a
=
Tính chất 3: Từ tỉ lệ thức
a c
b d
=
suy ra các tỉ lệ thức:
a b
c d
=
,
d c
b a
=
,
d b
c a
=
1.3. Tính chất của dãy tỉ số bằng nhau:
Tính chất 1: Từ tỉ lệ thức
a c
b d
=
suy ra
a c a c a c
b d b d b d
+ −
= = =
+ −
, (b ≠ ± d)
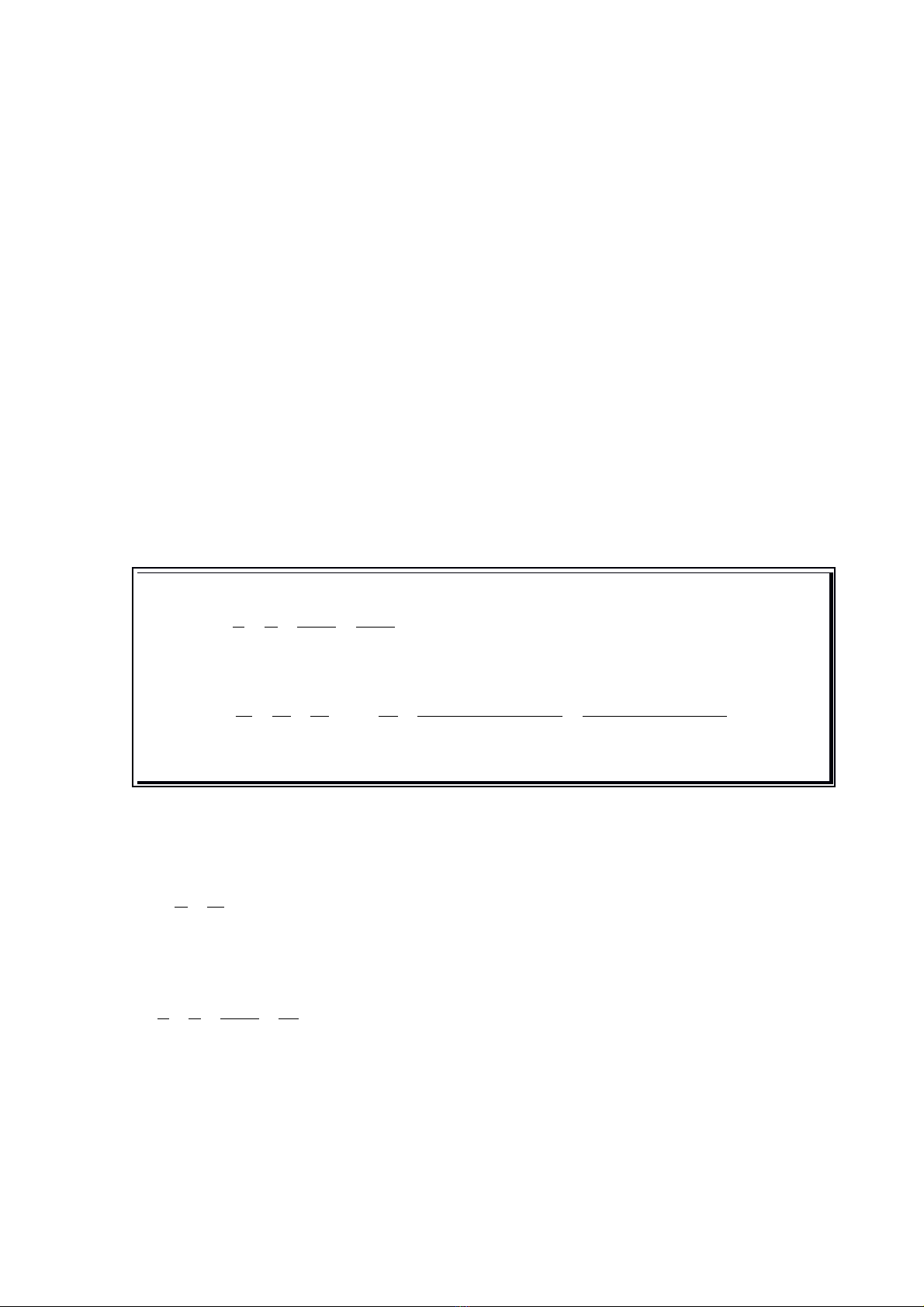
Tính chất 2: từ dãy tỉ số bằng nhau
ta suy ra: = = … (giả thiết các tỉ số đều có nghĩa)
Lưu ý: Tính chất trên còn mở rộng cho n số (n
2)
Nếu có
3
1 2
1 2 3
... n
n
a a
a a
b b b b
= = = =
thì
3 1 2 3
1 2
1 2 3 1 2 3
...
... .....
...
n n
n n
a a a a a a
a a
b b b b b b b b
+ + + +
= = = = = =
+ + + +
(gt các tỉ số đều nghĩa)
Nếu đặt dấu "-" trước số hạng trên của tỉ số nào thì đặt dấu"-"trước số hạng
dưới của tỉ số đó
.1.4. Một số tính chất của đẳng thức khác :
* A = B => AB=A2=B2
* A=B=C => ABC = A3 = B3 = C3
*
Giải pháp 2: Hệ thống dạng bài tập và cách giải
2. Nội dung bài tập vận dụng: Dạng toán về dãy tỉ số bằng nhau ở lớp 7 rất đa
dạng nhưng trong đề tài này tôi chỉ đề cập đến một số dạng từ cơ bản đến nâng
cao cụ thể như sau:
2.1: Một số dạng toán về dãy tỉ số bằng nhau:
Dạng 1: Các bài toán đơn giản áp dụng trực tiếp công thức dãy tỉ số bằng nhau
Dạng 2: Dạng áp dụng tính chất dãy tỷ số bằng nhau sau khi đã lập được các tỷ
số mới bằng các tỷ số đã cho để sử dụng dữ kiện đề bài
Dạng 3: Từ dự kiện đề bài cho biến đổi về dãy tỷ số bằng nhau để áp dụng tính
chất dãy tỷ số bằng nhau
Dạng 4: Dạng bài tập về dãy tỷ số bằng nhau mà phần điều kiện đề bài cho các
biến có dạng tích ( xy, xyz, …) hoặc có lũy thừa.
Dạng 5: Vận dụng tính chất dãy tỉ số bằng nhau để giải các bài toán có nội
dung thực tế và dạng toán dành cho học sinh khá ,giỏi
2.2: Chi tiết các dạng toán: Dạng1. Các bài toán đơn giản áp dụng trực tiếp
công thức dãy tỉ số bằng nhau
a. Lí thuyết:
Tính chất dãy tỉ số bằng nhau:
1)
a c a c a c
b d b d b d
+ −
= = =
+ −
2) =
3)
3 1 2 3 1 2 3
1 2
1 2 3 1 2 3 1 2 3
... ...
... ... ...
n n n
n n n
a a a a a a a a a aa a
b b b b b b b b b b b b
+ + + + − + + −
= = = = = =
+ + + + − + + −
Giả thiết các tỉ số đều có nghĩa.
b. Các bài tập áp dụng :
Bài 1: Tìm x,y,z biết.
a) và b) và
c
*
)
9
11
x
y=
và
60x y
+ =
d
*
) 7x = 4y và y – x =26
Giải: Áp dụng tính chất dãy tỉ số bằng nhau ta có:
a)
3.3 9
24 35.3 15
3 5 3 5 8
x
x y x y
y
= =
+
= = = = = =
+
Vậy: x=9 , y=15
b) và
Giải : Áp dụng tính chất dãy tỉ số bằng nhau ta có:
Vậy : x=-56 , y=-12 , z= -44
* Hướng dẫn:

Rèn luyện kĩ năng vận dụng tính chất dãy tỉ số bằng nhau vào một số bài toán lớp 7
c) Để sử dụng được giả thiết đề bài cho
60x y
+ =
Ta biến đổi từ
9
11
x
y=
suy ra
9 11
x y
=
d)Ta biến đổi từ 7x =4y suy ra
4 7
x y
=
Cách làm tương tư như phần a,b
Lưu ý: Biến đổi sao cho x và y ở cùng phía trên hoặc ở cùng phía dưới trong
dãy tỉ số bằng nhau
Bài 2: Tìm các số a,b,c,d biết rằng : a:b:c:d = 2:3:4:5 và a+b+c+d = -42
( BT79/22 sách bài tập toán 7)
Giải : Từ a:b:c:d = 2:3:4:5 => (tính chất dãy tỷ số bằng nhau )
=> a=-6 , b = -9 , c= -12 , d= -15
Vậy a=-6 ; b=-9 ;c= -12 ; d=-15
* Học sinh thường sai trong cách trình bày, chẳng hạn: Áp dụng tính chất dãy tỉ
số bằng nhau
Sai lầm là học dùng dấu “=>” thay cho dấu “=”
Lưu ý: Giáo viên cần khắc sâu để học sinh tránh gặp sai lầm khi giải toán
* Sau khi hướng dẫn học sinh làm bài tập tôi cho học sinh làm bài tương tự các
em hoạt động theo nhóm đôi ( hai bạn cùng bàn) theo phiếu số 1(phần phụ lục)
* Dạng 2: Dạng áp dụng tính chất dãy tỷ số bằng nhau sau khi đã lập được
các tỷ số mới bằng các tỷ số đã cho để sử dụng dữ kiện đề bài
a. Lí thuyết:
1)
2)
3) Khi cho a,b,c tỉ lệ với x,y,z =>
4) Nâng cao: Nếu thì
1 2 3
1 2 3
k a k c k e k
k b k d k f
+ + =
+ +
( k1,k2,k3
b. Các bài tập áp dụng :
Bài 1: Tìm x, y biết :
a) và b) và
Hướng dẫn suy luận: Đề bài cho nên từ dãy tỉ số ta phải biến đổi sao cho xuất
hiện tỉ số mới bằng tỉ số đã cho trong đó số hạng trên là 2y
Áp dụng tính chất dãy tỉ số bằng nhau:


























