
1
PHẦN I: ĐẶT VẤN ĐỀ
1.Lý do chọn đề tài.
Vật lý là môn khoa học thực nghiệm, khoa học tự nhiên, gây rất nhiều
hứng thú cho học sinh khi học tập và nghiên cứu nó. Nhưng cũng gây không ít
khó khăn khi học sinh chưa hiểu kỹ và sâu các vấn đề cơ bản. Đối với học sinh
khối lớp 12 liên quan trực tiếp đến các em ôn thi trung học phổ thông Quốc Gia
giáo viên trực tiếp giảng dạy cần phải tìm tòi, chịu khó và định hướng cho học
sinh cách học phù hợp và có hiệu quả. Đặc biệt là kì thi trung học phổ thông
quốc gia năm học 2018-2019 vừa qua việc phân loại đối tượng rất rõ ràng và
kiến thức trong mỗi câu hỏi yêu cầu học sinh cần phải nắm được, hiểu được mới
giải quyết được vấn đề. Trong hệ thống câu hỏi đó thì dạng bài tập đồ thị gây
khó khăn cho học sinh rất nhiều và những năm gần đây xu hướng kiểm tra dạng
bài tập này nhiều hơn vì mang đậm nét cho bài toán vật lý đồng thời yêu cầu học
sinh phải hiểu thực sự vấn đề mới giải quyết được.
Xuất phát từ thực tiễn dạy học nhiều năm ở trường THPT, đặc biệt liên quan
trực tiếp đến việc dạy ôn thi trung học phổ thông quốc gia, bản thân thấy việc học
sinh tiếp cận và giải quyết với dạng bài tập đồ thị rất bối rối và khó khăn vì thế để
hướng dẫn cho các em hiểu được và làm được những bài tương tự thì giáo viên
giảng dạy cần có một quy trình cụ thể từ điểm xuất phát đến khâu vận dụng.
Những năm gần đây xu thế ra đề thi trung học phổ thông quốc gia với câu
hỏi rất hay và khó nhằm phân loại đối tượng học sinh, đánh giá đúng đối tượng
dạy và học hiện nay đó là dạng bài toán về đồ thị. Nếu học sinh không được rèn
luyện nhiều, không được giải trước các dạng bài toán dạng này và không tư duy
được về quy luật giải bài tập thì không đủ thời gian để giải quyết các bài tập
trong thời gian làm bài thi dẫn đến kết quả không cao. Từ các yêu cầu đó mà bản
thân mạnh dạn lựa chọn nội dung: “Tư duy sáng tạo về bài toán đồ thị trong
phần dao động cơ của vật lý 12” làm đề tài nghiên cứu.
2. Mục đích nghiên cứu.
Đề tài nhằm tập trung nghiên cứu, phân tích lí thuyết và giải các bài tập để tìm
ra phương pháp chung giải quyết vấn đề, tạo tư duy suy luận sáng tạo từ dạng
bài toán cơ bản để giải được bài toán khác. Đề tài cũng giúp giáo viên, học sinh
nhận biết và giải quyết được các bài toán về đồ thị phần dao động cơ đồng thời
tạo hứng thú học tập cho học sinh và đạt kết quả tốt cho quá trình học tập .
3. Đối tượng nghiên cứu.
- Là giáo viên, giáo viên bồi dưỡng học sinh thi trung học phổ thông quốc gia.
- Học sinh ôn thi trung học phổ thông quốc gia.
- Các cá nhân khác quan tâm đến bài toán đồ thị trong vật lý.

2
4. Phạm vi nghiên cứu.
- Bài toán về đồ thị trong phần dao động cơ học của chương trình vật lý 12.
- Phân dạng đồ thị của một số đại lượng mà học sinh đã học trong chương trình
và tư duy sáng tạo giải các dạng đồ thị khác.
- Bài toán cho đồ thị, dựa vào đồ thị xác định các đại lượng khác.
- Tạo tư duy sáng tạo để học sinh phát triển và hình thành quy luật cách phát
triển bài toán từ bài toán cơ bản.
5. Phương pháp nghiên cứu.
+ Dùng cơ sở lý luận của phương pháp giải bài tập vật lý.
+ Xây dựng các kiến thức định tính, định lượng bằng kiến thức toán học và vật lý.
+ Áp dụng vào hệ thống các bài tập trong phần dao động cơ của vật lý 12
+ Khảo sát thực nghiệm kết quả ở đối tượng ôn thi trung học phổ thông quốc gia
môn vật lý cùng với giáo viên dạy môn vật lý 12.
+ Đánh giá hiệu quả của đề tài thông qua kết quả thu được từ học sinh, giáo viên dạy
vật lý và tiến hành khảo sát, đối chứng kết quả thu được so với kết quả ban đầu.
6. Kế hoạch thực hiện
+ Ngày (02,04)/11/2019 triển khai phiếu đánh giá thực trạng dạy và học về bài toán đồ
thị vật lý đối với học sinh lớp 12 và giáo viên dạy vật lý ở 3 trường trung học phổ
thông trên địa bàn tỉnh Nghệ An.
+ Ngày 11/11/2019 triển khai đề tài cho những giáo viên có dạy vật lý 12 ở ba trường
+ Từ 22/11/2019 đến 28/12/2019 giáo viên áp dụng đề tài dạy cho một số lớp 12
+ Từ 30/12/2019 đến 11/01/2020 khảo sát lấy ý kiến giáo viên sau khi đã nghiên cứu
và áp dụng đề tài đồng thời khảo sát nhận xét từ học sinh các lớp có giáo viên áp dụng
đề tài và các lớp không sử dụng đề tài.
+ Từ 12/1/2020 đến 15/01/2020 tổng hợp thông tin nhận xét từ giáo viên và học sinh
để từ đó đánh giá về hiệu quả của đề tài.
7. Đóng góp của đề tài
Thông qua dạy học nhận thấy những khó khăn từ học sinh về bài toán đồ thị
trong môn vật lý vì thế tôi đã tìm tòi nghiên cứu để khắc phục khó khăn đó. Đề
tài này hoàn toàn được rút ra từ kinh nghiệm bản thân trong quá trình dạy học,
thể hiện được tính mới và đóng góp của đề tài cho bộ môn là:
+ Góp phần tạo hứng thú học tập cho môn vật lý
+ Làm tăng khả năng tư duy sáng tạo trong quá trình học tập
+ Làm tăng hiệu quả cho học sinh thi trung học phổ thông quốc gia môn vật lý
+ Là tài liệu bổ ích cho giáo viên dạy vật lý và học sinh luyện thi trung học phổ
thông quốc gia.
3
PHẦN II: NỘI DUNG
I. Cơ sở khoa học
1.Cơ sở lý luận
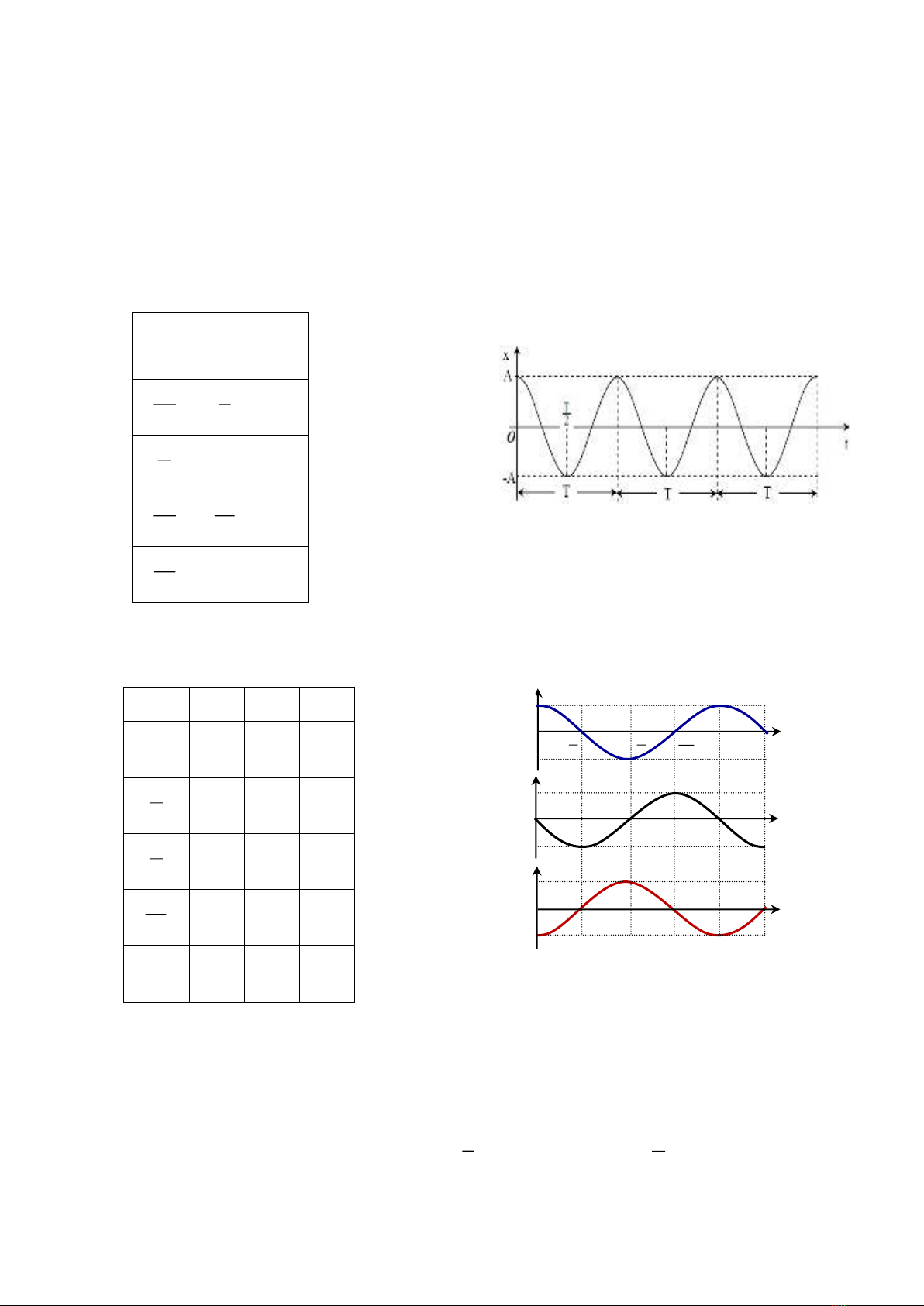
1.1. Đồ thị dao động cơ
Xét phương trình dao động
x Acos( t )
= +
, chọn gốc thời gian và chiều
dương trục tọa độ thích hợp sao cho φ = 0. Lập bảng biến thiên của li độ x theo
thời gian và đồ thị biểu diễn x theo t như sau:
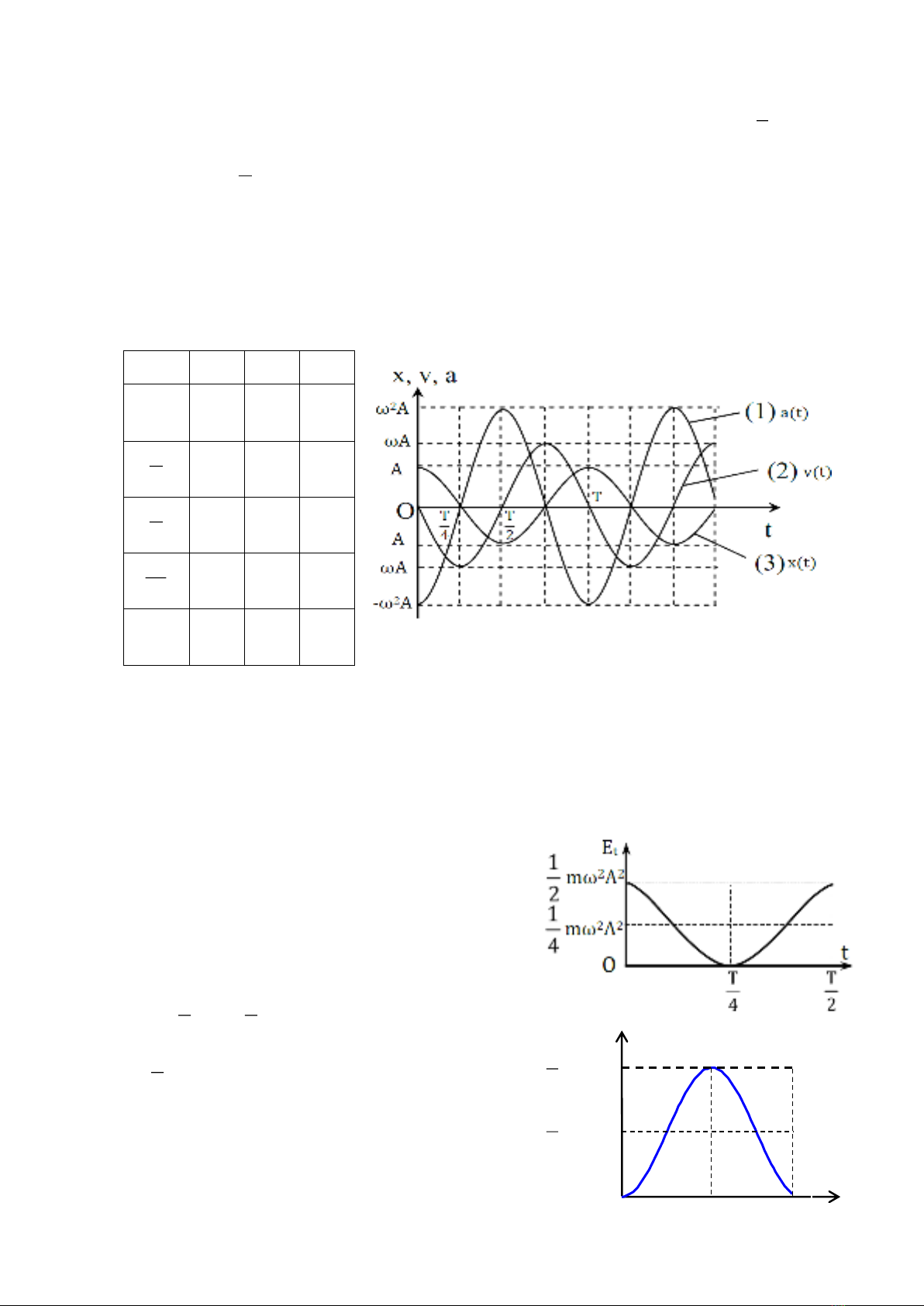
1.2. Đồ thị và sự so sánh pha của các dao động điều hòa: x, v, a.
Vẽ đồ thị của dao động
x Acos( t )= +
trong trường hợp φ = 0.
Nhận xét:
+ Nếu dịch chuyển đồ thị v về phía chiều dương của trục Ot một đoạn T/4 thì
đồ thị của v và x cùng pha nhau.
Nghĩa là, v nhanh pha hơn x một góc
2
hay về thời gian là
T
4
.
t
ωt
x
0
0
A
2
2
0
A−
3
2
3
2
0
2
2
A
t
x
v
a
0
A
0
2
A−
T
4
0
A−
0
T
2
A−
0
2
A
3T
4
0
A
0
T
A
0
2
A−
Đồ thị biểu diễn li độ
x Acos( t )= +
với
0=
x
v
a
t
t
t
T
2
T
4
T
4
3T
O
O
O
A
-A
Aω
-A
-A2
A2
4
+ Nếu dịch chuyển đồ thị a về phía chiều dương của trục Ot một đoạn T/4 thì
đồ thị của a và v cùng pha nhau. Nghĩa là, a nhanh pha hơn v một góc
2
hay về
thời gian là
T
4
.
+ Nhận thấy a và x luôn ngược pha nhau (trái dấu nhau).
+ Biên độ của li độ là A, biên độ của vận tốc
.A
và biên độ của gia tốc
2.A
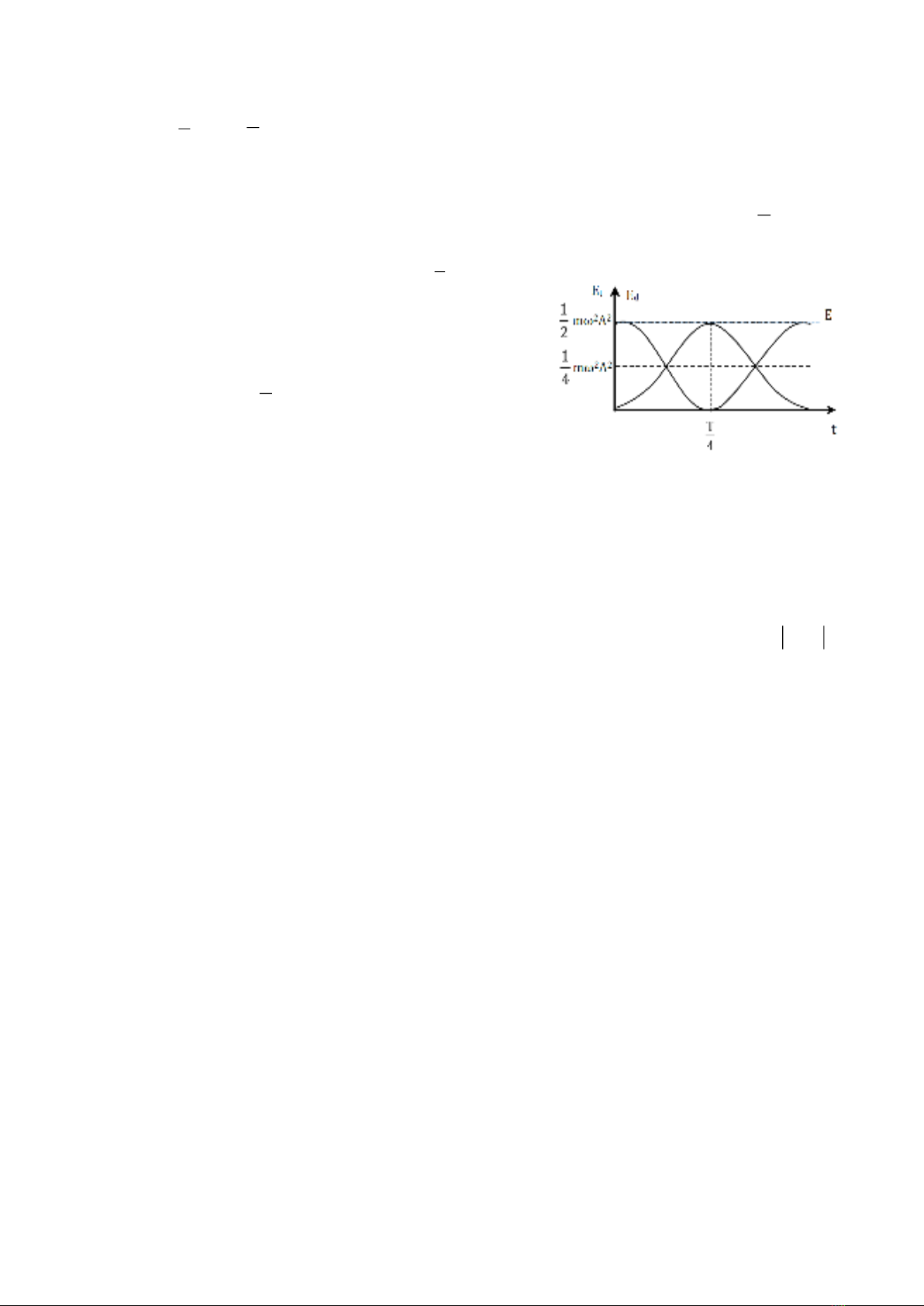
1.3. Đồ thị x, v và a dao động điều hòa vẽ chung trên một hệ trục tọa độ
Vẽ đồ thị trong trường hợp φ = 0.
1.4. Đồ thị năng lượng trong dao động điều hòa
1.4.1. Sự bảo toàn cơ năng
Dao động của con lắc đơn và con lắc lò xo dưới tác dụng của lực thế (trọng lực
và lực đàn hồi, …) và không có ma sát nên cơ năng của nó được bảo toàn. Vậy
cơ năng của vật dao động được bảo toàn.
1.4.2. Biểu thức thế năng
+ Xét con lắc lò xo. Tại thời điểm bất kỳ vật
có li độ
x Acos( t )
= +
và thế năng của
con lắc lò xo có dạng:
2 2 2
11
E kx kA cos ( t )
t22
= = +
2 2 2
1m A cos ( t )
2
= +
+ Ta có đồ thị Et phụ thuộc vào thời gian
trong trường hợp φ = 0.
1.4.3. Biểu thức động năng
t
x
v
a
0
A
0
2
A−
T
4
0
A−
0
T
2
A−
0
2
A
3T
4
0
A
0
T
A
0
2
A−
Eđ
O
T/4
T/2
22
1mA
2
22
1mA
4
t
5
+ Ở thời điểm t bất kì vật có vận tốc
v Asin( t )= − +
và có động năng
2
d
1
= mv
2
E=
2 2 2
1mω A sin (ωt + φ)
2
+ Ta có đồ thị Eđ phụ thuộc vào thời gian trong trường hợp φ = 0.
+ Như vậy động năng và thế năng biến thiên tuần hoàn với chu kỳ
1
T
T2
=
(với T
là chu kỳ dao động) và có biên độ
22
4
1mA
1.4.4. Biểu thức cơ năng
+ Cơ năng tại thời điểm t:
22
d
1
E = E + E m A
t2
=
+ Ta có đồ thị Eđ và Et phụ thuộc vào thời gian
vẽ trên cùng một hệ trục.
1.5. Đồ thị lực đàn hồi và lực kéo về trong dao động điều hòa
1.5.1. Đồ thị lực đàn hồi
+ Lực đàn hồi trong dao động điều hòa của con lắc lò xo phụ thuộc vào chiều
dài của lò xo
dh 0
F k(l l )
=−
thì đồ thị là một đoạn thẳng.
+ Đồ thị độ lớn lực đàn hồi của lò xo phụ thuộc vào chiều dài lò xo
dh 0
F k l l=−
là đoạn thẳng gấp khúc
+ Lực đàn hồi của lò xo phụ thuộc vào li độ x ta có
dh
F k( l x)
= +
đồ thị cũng
là đoạn thẳng (
l
là độ biến dạng của lò xo khi cân bằng)
+ Lực đàn hồi của lò xo phụ thuộc vào thời gian ta có
dh
F k( l Acos( t ))
= + +
đồ thị là đường biến thiên tuần hoàn
1.5.2. Đồ thị lực kéo về
+ Lực kéo về phụ thuộc vào li độ x Fkv= - k.x đồ thị là đoạn thẳng đi qua gốc tọa độ.
+ Nếu lực kéo về phụ thuộc vào thời gian thì ta được hàm số
kv
F kAcos( t )
= − +
thì ta được đồ thị hàm biến thiên điều hòa theo thời gian.
2. Cơ sở thực tiễn
2.1. Thực trạng dạy và học về bài toán đồ thị vật lý.
2.1.1. Về phía giáo viên
Bài toán đồ thị là bài toán đòi hỏi học sinh vận dụng kiến thức tổng hợp,
có khả năng phân tích, đọc đồ thị mới giải quyết được vấn đề. Để giúp học sinh
giải quyết tốt các bài toán đồ thị, giáo viên cần chịu khó tìm tòi hệ thống bài tập
và hình thành phương pháp giảỉ bài toán có hiệu quả. Tuy nhiên hiện nay các tài
liệu về bài toán đồ thị trong vật lí không nhiều, giáo viên chưa thực sự sẵn sàng
thực hiện chuyên đề về bài toán đồ thị cho học sinh thậm chí có những giáo viên
còn e ngại các bài toán về đồ thị.
T/2






















