
PH L C I: Ụ Ụ M U PHI U ĐĂNG KÝ SÁNG KI NẪ Ế Ế
C NG HÒA XÃ H I CH NGHĨA VI T NAMỘ Ộ Ủ Ệ
Đc l p - T do - H nh phúcộ ậ ự ạ
PHI U ĐĂNG KÝ SÁNG KI NẾ Ế
1. H và tên ng i đăng ký:ọ ườ NGUY N TU N ANHỄ Ấ
2. Ch c v : ứ ụ T tr ng chuyên môn – T V t lý - KTCN ổ ưở ổ ậ
3. Đn v công tác: Tr ng THPT Chuyên Tho i Ng c H uơ ị ườ ạ ọ ầ
4. Nhi m v đc giao trong đn v : Qu n lý t chuyên môn và gi ng d y kh i 10 - 12ệ ụ ượ ơ ị ả ổ ả ạ ố
5. Tên đ tài sáng ki n: Chuyên đ v t lý hi n đi:ề ế ề ậ ệ ạ “THUY T T NG ĐI H PẾ ƯƠ Ố Ẹ
TRONG CÔNG TÁC B I D NG H C SINH GI IỒ ƯỠ Ọ Ỏ ".
6. Lĩnh v c đ tài sáng ki n: ự ề ế
Ph c v gi ng d y môn v t lý trong công tác b i d ng h c sinh gi i đi v i h c sinhụ ụ ả ạ ậ ồ ưỡ ọ ỏ ố ớ ọ
trung h c ph thông.ọ ổ
7. Tóm t t n i dung sáng ki n: N i dung sáng ki n g m có hai ph n chínhắ ộ ế ộ ế ồ ầ
* C s lý thuy t v v t lý hi n đi.ơ ở ế ề ậ ệ ạ
* V n d ng gi i các bài t p t c b n đn các đ thi h c sinh gi i c p qu c gia.ậ ụ ả ậ ừ ơ ả ế ề ọ ỏ ấ ố
8. Th i gian, đa đi m, công vi c áp d ng sáng ki n:ờ ị ể ệ ụ ế
* Th i gian v n d ng sáng ki n năm h c 2015 – 2019.ờ ậ ụ ế ọ
* Công vi c áp d ng cho b i d ng h c sinh gi i c p khu v c và Qu c gia. ệ ụ ồ ưỡ ọ ỏ ấ ự ố
9. Các đi u ki n c n thi t đ áp d ng sáng ki n:ề ệ ầ ế ể ụ ế
H c sinh ph i n m trong đi tuy n h c sinh gi i.ọ ả ằ ộ ể ọ ỏ
10. Đn v áp d ng sáng ki n: Tr ng THPT Chuyên Tho i Ng c H u.ơ ị ụ ế ườ ạ ọ ầ
11. K t qu đt đcế ả ạ ượ : (L i ích kinh t , xã h i thu đc)ợ ế ộ ượ
H c sinh n m b t ki n th c t t đ ph c v cho các k thi h c sinh gi i nêu trên và đãọ ắ ắ ế ứ ố ể ụ ụ ỳ ọ ỏ
đem l i khá nhi u k t qu t t (đc nêu ph n cu i sáng ki n – trang 50).ạ ề ế ả ố ượ ở ầ ố ế
An Giang, ngày 09 tháng 02 năm 2019
Tác giả
Nguy n Tu n Anhễ ấ
SKKN 2018 - 2019 GV: Nguy n Tu n Anhễ ấ 1

PH L C II: Ụ Ụ M U BÁO CÁO K T QU SÁNG KI NẪ Ế Ả Ế
S GIÁO D C VÀ ĐÀO T OỞ Ụ Ạ
TR NG THPT CHUYÊNƯỜ
THO I NG C H UẠ Ọ Ầ
C NG HÒA XÃ H I CH NGHĨA VI T NAMỘ Ộ Ủ Ệ
Đc l p - T do - H nh phúcộ ậ ự ạ
An giang, ngày 09 tháng 02 năm 2019
BÁO CÁO
K t qu th c hi n sáng ki n, c i ti n, ế ả ự ệ ế ả ế gi i pháp k thu t, qu n lý, tác nghi pả ỹ ậ ả ệ , ngứ
d ng ti n b k thu tụ ế ộ ỹ ậ ho c nghiên c u khoa h c s ph m ng d ng ặ ứ ọ ư ạ ứ ụ
I. S L C LÝ L CH TÁC GI .Ơ ƯỢ Ị Ả
- H và tên: NGUY N TU N ANHọ Ễ Ấ Nam, n : Namữ
- Ngày tháng năm sinh: 20/09/1973
- N i th ng trú: ơ ườ 12G3 - H Bi u Chánh - Bình Khánh - TP. Long Xuyên - An Giangồ ể
- Đn v công tác: ơ ị Tr ng THPT Chuyên Tho i Ng c H uườ ạ ọ ầ
- Ch c v hi n nay: T tr ng chuyên môn – T V t lý - KTCNứ ụ ệ ổ ưở ổ ậ
- Trình đ chuyên môn: Th c sộ ạ ỹ
- Lĩnh v c công tác: D y h cự ạ ọ
II. S L C ĐC ĐI M TÌNH HÌNH ĐN V .Ơ ƯỢ Ặ Ể Ơ Ị
- Tr ng THPT Chuyên Tho i Ng c H u là tr ng đng đu c a T nh An Giang v ch tườ ạ ọ ầ ườ ứ ầ ủ ỉ ề ấ
l ng gi ng d y và đào t o ngu n nhân l c cho t nh nhà.ượ ả ạ ạ ồ ự ỉ
- Luôn đc s quan tâm và ch đo sâu sát c a các c p lãnh đo, các c quan ban ngành ượ ự ỉ ạ ủ ấ ạ ơ
và đc bi t là s quan tâm c a các b c ph huynh h c sinh v ch t l ng gi ng d y và ặ ệ ự ủ ậ ụ ọ ề ấ ượ ả ạ
đu t c s v t ch t ph c v cho gi ng d y và h c t p c a các em h c sinh. ầ ư ơ ở ậ ấ ụ ụ ả ạ ọ ậ ủ ọ
- Tên sáng ki n:ế Chuyên đ v t lý hi n đi:ề ậ ệ ạ “THUY T T NG ĐI H P TRONGẾ ƯƠ Ố Ẹ
CÔNG TÁC B I D NG H C SINH GI IỒ ƯỠ Ọ Ỏ ".
- Lĩnh v c: Ph c v gi ng d y môn v t lý trong công tác b i d ng h c sinh gi i đi v i ự ụ ụ ả ạ ậ ồ ưỡ ọ ỏ ố ớ
h c sinh trung h c ph thông.ọ ọ ổ
III. M C ĐÍCH YÊU C U C A Đ TÀI, SÁNG KI N.Ụ Ầ Ủ Ề Ế
1. Th c tr ng ban đu tr c khi áp d ng sáng ki n:ự ạ ầ ướ ụ ế
Trong công tác b i d ng h c sinh gi i, ngoài vi c truy n đt ki n th c, k năng phânồ ưỡ ọ ỏ ệ ề ạ ế ứ ỹ
tích gi i bài t p, cho ki m tra c sát th c t ..., còn m t v n đ h t s c quan tr ng là giúp cácả ậ ể ọ ự ế ộ ấ ề ế ứ ọ
em tìm ra qui lu t (ph ng pháp) gi i toán.ậ ươ ả
Lĩnh v c V t lý hi n đi là m t lĩnh v c r ng và khó vì th yêu c u trên l i càng r tự ậ ệ ạ ộ ự ộ ế ầ ạ ấ
c n đi v i các em h c sinh. Đng tr c khó khăn trên, sau m t th i gian ti p c n v i côngầ ố ớ ọ ứ ướ ộ ờ ế ậ ớ
SKKN 2018 - 2019 GV: Nguy n Tu n Anhễ ấ 2
tác b i d ng h c sinh gi i, tôi xin đc trình bày suy nghĩ c a mình v vi c gi i quy t cácồ ưỡ ọ ỏ ượ ủ ề ệ ả ế
bài t p trong lĩnh v c v t lý hi n đi (ậ ự ậ ệ ạ THUY T T NG ĐI H P)Ế ƯƠ Ố Ẹ .
2. S c n thi t ph i áp d ng sáng ki n:ự ầ ế ả ụ ế
Giúp h c sinh có đnh h ng t t đ gi i quy t các bài t p có nh ng ki n th c liên quan.ọ ị ướ ố ể ả ế ậ ữ ế ứ
T o đng l c cho các em h c sinh ham h c, yêu thích b môn và say mê nghiên c u.ạ ộ ự ọ ọ ộ ứ
3. N i dung sáng ki n:ộ ế
3.1. C s lý thuy t:ơ ở ế
3.1.1. Các tiên đ Anhxtanh:ề
a. Tiên đ 1ề (nguyên lý t ng đi): ươ ố
Các đnh lu t v t lý (c h c - ví d đnh lu t II Newton, đi n t h c,…) có cùng m t d ngị ậ ậ ơ ọ ụ ị ậ ệ ừ ọ ộ ạ
nh nhau trong m i h quy chi u (HQC) quán tính. Nói cách khác, hi n t ng v t lý di n raư ọ ệ ế ệ ượ ậ ễ
nh nhau trong các HQC quán tính.ư
b. Tiên đ 2ề (nguyên lý v s b t bi n c a t c đ ánh sáng):ề ự ấ ế ủ ố ộ
T c đ c a ánh sáng trong chân không có cùng đ l n b ng c trong m i HQC quán tính,ố ộ ủ ộ ớ ằ ọ
không ph thu c vào ph ng truy n và vào t c đ c a ngu n sáng hay máy thu: c = 3ụ ộ ươ ề ố ộ ủ ồ .108
m/s.
Nh n m nhấ ạ : C h c Newton (c h c c đi n) ch áp d ng đc cho v t chuy n đng có vơ ọ ơ ọ ổ ể ỉ ụ ượ ậ ể ộ
<< c (v n t c ánh sáng). C h c t ng đi tính còn g i là thuy t t ng đi h p do ậ ố ơ ọ ươ ố ọ ế ươ ố ẹ Einstein
xây d ng, áp d ng đc cho c các v t chuy n đng c v n t c ánh sáng và tr ng h p vự ụ ượ ả ậ ể ộ ỡ ậ ố ườ ợ
<< c là tr ng h p gi i h n (tr v c h c c đi n).ườ ợ ớ ạ ở ề ơ ọ ổ ể
Ví d : máy bay có đèn pha, nó đang chuy n đng. Máy bay chuy n đng và b n đn thì t cụ ể ộ ể ộ ắ ạ ố
đ viên đn đi v i ng i ng i trong máy bay khác t c đ viên đn đi v i ng i đng ộ ạ ố ớ ườ ồ ố ộ ạ ố ớ ườ ứ ở
sân bay. Nh ng t c đ ánh sáng mà đèn pha chi u t máy bay nh nhau đi v i c ư ố ộ ế ừ ư ố ớ ả hai ng iườ
nói trên.
3.1.2. Đng h c t ng đi tính:ộ ọ ươ ố
3.1.2.1. Công th c bi n đi Lorentz (Lo-ren-x ):ứ ế ổ ơ
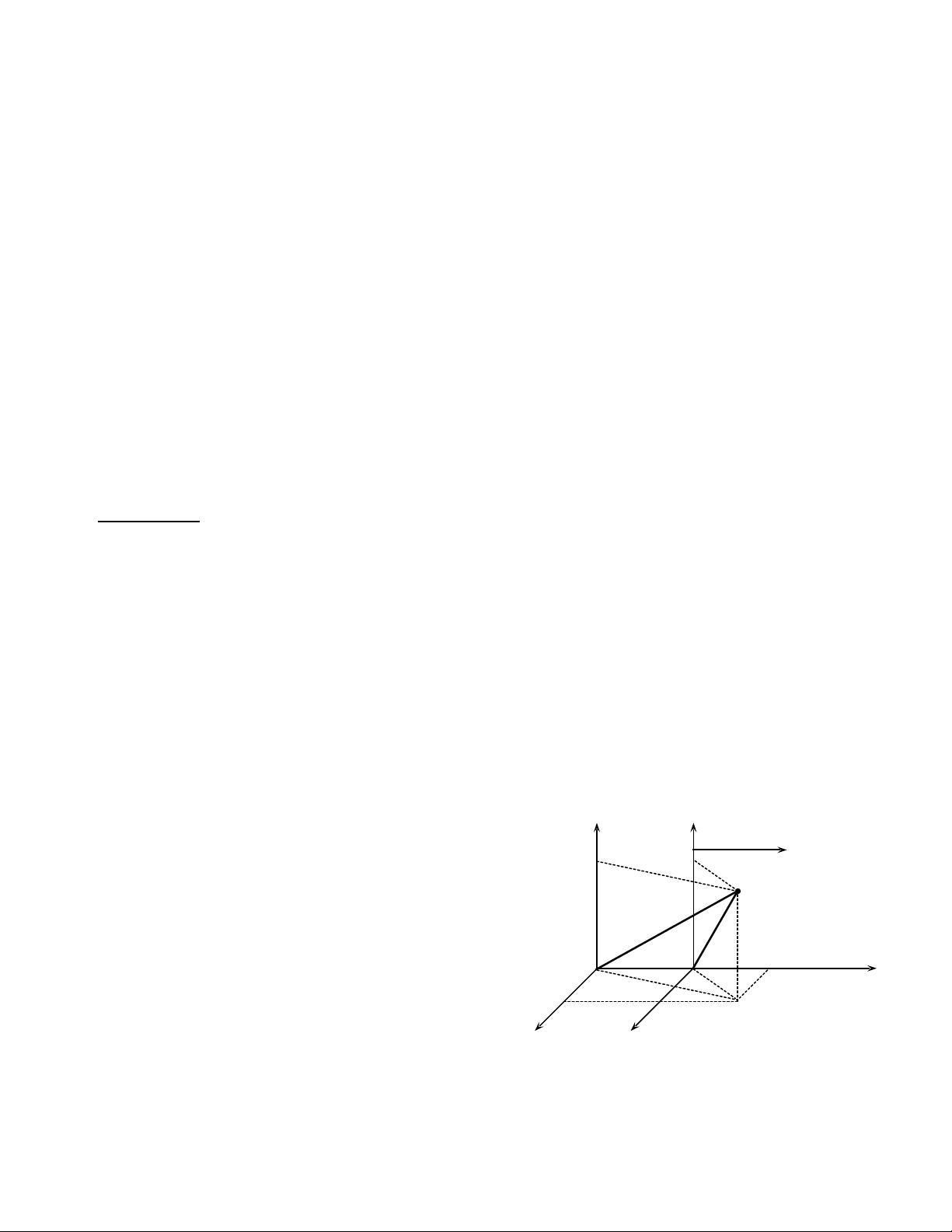
Trong c h c c đi n, khi xét v t chuy n đngơ ọ ổ ể ậ ể ộ
th ng, HQC O’ chuy n đng v i v n t c vẳ ể ộ ớ ậ ố
theo h ng x c a HQC O thì x’= x - vt, t’ = t vàướ ủ
d n đn công th c c ng v n t cẫ ế ứ ộ ậ ố
13 12 23
v v v= +
r r r
. Công th c đó không phù h pứ ợ
trong c h c t ng đi tính.ơ ọ ươ ố (Ví d tàu vũ trụ ụ
t c đ 0.6c, phát sóng tín hi u th ng v phíaố ộ ệ ẳ ề
tr c nó, theo cách tính c đi n thì v n t cướ ổ ể ậ ố
c a tín hi u đi v i quan sát viên trên Trái Đtủ ệ ố ớ ấ
là 1,6 c > c.)
Lorentz tìm đc các công th c li n h gi aượ ứ ệ ệ ữ
các t a đ c a cùng m t đi m và th i gian xét trong hai HQC quán tính khác nhau, đng th iọ ộ ủ ộ ể ờ ồ ờ
th a mãn yêu c u c a thuy t t ng đi ỏ ầ ủ ế ươ ố Einstein.
Xét hai HQC quán tính: Oxyz g n v i K, O’x’y’z’ g n v i K’. Ban đu O trùng O’. H Kắ ớ ắ ớ ầ ệ
đng yên. H K’ chuy n đng v i v n t c ứ ệ ể ộ ớ ậ ố
v
r
theo ph ng Ox đi v i h K. Theo thuy tươ ố ớ ệ ế
SKKN 2018 - 2019 GV: Nguy n Tu n Anhễ ấ 3
M
X
X’
Y’
Z’
Z
Y
OO’
zz'
yy'
x
x'
KK’
v
r

t ng đi th i gian trôi trong hai h s khác nhau: t khác t’. M t đi m M xét trong h K’ươ ố ờ ệ ẽ ộ ể ệ có
t a đ x’, trong h K là x. C n bi u di n x’ theo x,ọ ộ ệ ầ ể ễ t; và ng c l i x theo x’, t’. ượ ạ
T K sang K’:ừ
2
2 2
x vt t vx / c
x ' ;t ' ;y ' y;z ' z.
1 1
− −
= = = =
−β −β
T K’ sang K (chú ý t các công th c phía trên v i v thay b i –v):ừ ừ ứ ớ ở
2
2 2
x ' vt ' t ' vx '/ c
x ;t ;y y';z z ',
1 1
+ +
= = = =
−β −β
v i ớ
v / c
β =
.
* Chú ý: C h c t ng đi tính ơ ọ ươ ố (tr v ) c h c c đi n khi v/c ở ề ơ ọ ổ ể 0.
T công th c trên th y khi v/c ừ ứ ấ 0 thì x’= x - vt; t’ = t.
3.1.2.2. Các hi u ng t ng đi tính:ệ ứ ươ ố
T các công th c bi n đi Lorenừ ứ ế ổ tz, có th suy ra m t s h qu v tính ch t c a không gian-ể ộ ố ệ ả ề ấ ủ
th i gian, g i là các hi u ng t ng đi tính (chúng k l theo quan đi m c đi n nh ng đãờ ọ ệ ứ ươ ố ỳ ạ ể ổ ể ư
đc th c nghi m ki m ch ng tính đúng đn)ượ ự ệ ể ứ ắ .
3.1.2.3. Khái ni m v tính đng th i và quan h nhân qu gi a các bi n c hai n i xaệ ề ồ ờ ệ ả ữ ế ố ở ơ
nhau:
a. Khái ni m bi n c :ệ ế ố là m t hi n t ng (ví d viên đn t i đích).ộ ệ ượ ụ ạ ớ
Trong HQC quán tính K có hai bi n c A1(xế ố 1,y1,z1,t1) và A2(x2,y2,z2,t2). Th i đi m x y ra haiờ ể ả
bi n c trong h K là tế ố ệ 1, t2; nh ng trong h K’ t ng ng là t’ư ệ ươ ứ 1, t’2. Ta c n tìm kho ng th iầ ả ờ
gian t’2 - t’1.
T công th c bi n đi Lorenừ ứ ế ổ tz (t’1 theo t1, x1; t’2 theo t2, x2) ta thu đc:ượ
2 1 2 1
2
2 1 2
v
t t (x x )
c
t ' t ' .
1
− − −
− = −β
T công th c này th y: n u từ ứ ấ ế 2 - t1 = 0 nh ng xư2 - x1 khác 0 thì t’2 - t’1 khác 0. Đi u đó có nghĩa:ề
Hai bi n c x y ra đng th i trong h K thì s không đng th i trong h K’ tr khi trongế ố ả ồ ờ ệ ẽ ồ ờ ệ ừ
K chúng x y ra đng th i t i đi m có cùng t a đ x t c là xả ồ ờ ạ ể ọ ộ ứ 1 = x2 (t a đ yọ ộ 1 (z1) có th khácể
y2 (z2) vì K’ d ch chuy n d c tr c x, th i gian t không ph thu c vào t a đ y (z))ị ể ọ ụ ờ ụ ộ ọ ộ .
V y theo thuy t t ng đi, khái ni m đng th i ch là khái ni m t ng đi: trong HQC nàyậ ế ươ ố ệ ồ ờ ỉ ệ ươ ố
thì hai bi n c x y ra đng th i nh ng có th là không đng th i trong HQC khác.ế ố ả ồ ờ ư ể ồ ờ
T công th c trên, tr ng h p từ ứ ườ ợ 1 = t2, d u c a t’ấ ủ 2 - t’1 ph thu c d u c a xụ ộ ấ ủ 2 - x1 (v c đnh).ố ị
Nh v y th t các bi n c A1, A2 trong K’ ph thu c vào d u c a xư ậ ứ ự ế ố ụ ộ ấ ủ 2 – x1.
* Chú ý: k t lu n trên ế ậ không áp d ng cho các bi n c có liên h nhân quụ ế ố ệ ả v i nhau (nguyênớ
nhân bao gi cũng x y ra tr c k t qu ).ờ ả ướ ế ả
b. S co ng n Lorenự ắ tz (co đ dài):ộ
Chúng ta c n tr l i câu h i: đ dài c a m t v t trong h K, K’ có nh nhau không?ầ ả ờ ỏ ộ ủ ộ ậ ệ ư
Bài toán: có m t th c đng yên trong K’, đt d c tr c x’, đ dài c a th c là x’ộ ướ ứ ặ ọ ụ ộ ủ ướ 2 - x’1, đt làặ
0
l
. Hãy tìm đ dài c a th c trong h K?ộ ủ ướ ệ
Gi iả: đ dài c a th c trong h K là hi u t a đ xộ ủ ướ ệ ệ ọ ộ 2, x1 c a hai đu th c trong h K ủ ầ ướ ệ t iạ
cùng m tộ th i đi mờ ể : l = x2 - x1.
SKKN 2018 - 2019 GV: Nguy n Tu n Anhễ ấ 4

Áp d ng công th c bi n đi Lorentz: ụ ứ ế ổ
2
x vt
x '
1
−
=−β
, v i tớ1 = t2 = t
2 1
2 1 2
x x
x ' x '
1
−
− = −β
02
1β
l
l=−
v i ớ
2
1
1
γ = −β
.
Nh n xét: ậl < l0.
Tóm l iạ:
Trong K’ (O’ đo th c): th c đng yên, có chi u dài ướ ướ ứ ề
0
l
Trong K (O đo th c): th c chuy n đng, có chi u dài ướ ướ ể ộ ề l.
Ta v a ch ng minh đc ừ ứ ượ l <
0
l
, v yậ đ dài (d c theo ph ng chuy n đng) c a m t v tộ ọ ươ ể ộ ủ ộ ậ
trong HQC mà nó chuy n đng NG N h n đ dài c a v t trong HQC mà nó đng yên (khiể ộ Ắ ơ ộ ủ ậ ứ
v t chuy n đng, kích th c c a nó b co ng n theo ph ng chuy n đng, m c co ng n tùyậ ể ộ ướ ủ ị ắ ươ ể ộ ứ ắ
thu c t c đ chuy n đng c a v t).ộ ố ộ ể ộ ủ ậ
c. Dãn th i gian: (ờKho ng th i gian c a cùng m t quá trình trong hai h K, K’ nh th nào?)ả ờ ủ ộ ệ ư ế
Bài toán: có m tộ đng h đng yên trong K’. Ta xét hai bi n c x y ra t i cùng m t đi m cóồ ồ ứ ế ố ả ạ ộ ể
t a đ x’ trong K’. Kho ng th i gian gi a ọ ộ ả ờ ữ hai bi n c trong K’ là t’ế ố 2 - t’1. C n tìm kho ng th iầ ả ờ
gian gi a hai bi n c này trong h K, t c tìm tữ ế ố ệ ứ 2 - t1.
Áp d ng công th c bi n đi Lorentz: ụ ứ ế ổ
2
2
t ' vx '/ c
t
1
+
=−β
v i x’ớ1 = x’2 = x’
2 1
2 1 2
t ' t '
t t
1
−
− = −β
.
Đt ặ
2 1 0 2 1
t t t , t t ' t '∆ − ∆ −
, v y: ậ
2
0
t t 1∆ = ∆ −β
.
Nh n xét: ậ
0
t t∆ < ∆
. Hay vi t cách khác: ế
2
0
t t 1 t
∆ = ∆ −β < ∆
. (
0
t∆
trong h K’ệ.)
0
t t
∆ < ∆
=> N u g n m t đng h vào h K và m t đng h vào h K’ thì đng h trong hế ắ ộ ồ ồ ệ ộ ồ ồ ệ ồ ồ ệ
K ch y nhanh h n đng h trong h K’. Đó là tính t ng đi c a th i gian.ạ ơ ồ ồ ệ ươ ố ủ ờ
(Khái ni m th i gian riêng: N u h t đng yên trong HQC nào đó, th i gian s ng đo đcệ ờ ế ạ ứ ờ ố ượ
trong HQC đó là th i gian riêng.)ờ
Tr ng h p gi i h n: v<<c thì ườ ợ ớ ạ
0
t t
∆ ∆
tr l i c h c c đi n, kho ng th i gian là tuy tở ạ ơ ọ ổ ể ả ờ ệ
đi.ố
Tóm l iạ:
- Hi u ng cệ ứ o đ dài t c là: ộ ứ l <
0
l
(l đo b i O, ở
0
l
đo b iở O’) v i chú ý xét tớ1 = t2.
- Hi u ng dệ ứ ãn th i gian t c là: ∆ờ ứ t > ∆t0 (∆t đo b i O, ở∆t0 đo b iở O’) v i chú ý x’ớ1 = x’2.
d. Quãng đng đi và th i gian đi c a ánh sáng:ườ ờ ủ
Gi s ánh sáng đi cùng chi u v i v n t c c a K’ đi v i K, qua v trí x’ả ử ề ớ ậ ố ủ ố ớ ị 1 lúc t’1.
* Quãng đng đi c a ánh sáng:ườ ủ
Ta không áp d ng đc công th c co đ dài trong m c ụ ượ ứ ộ ụ (2.b) khi tính quãng đng đi c a ánhườ ủ
sáng vì quãng đng đi c a ánh sáng không gi ng chi u dài c a th c. T a đ xườ ủ ố ề ủ ướ ọ ộ 1, x2 c a haiủ
đu th c có th đo cùng th i đi m nh ng đ ánh sáng truy n t xầ ướ ể ở ờ ể ư ể ề ừ 1 đn xế2 thì m t th iấ ờ
gian nên không th đo cùng m t th i đi m.ể ở ộ ờ ể
Ta s ch ng minh th c ch t quãng đng đi c a ánh sáng không co l i mà dãn ra.ẽ ứ ự ấ ườ ủ ạ
Quãng đng đi c a ánh sáng trong h K’ là ườ ủ ệ
2 1
x ' c(t ' t ')∆ = −
.
Quãng đng đi c a ánh sáng trong h K là ườ ủ ệ
2 1
x c(t t )∆ = −
.
SKKN 2018 - 2019 GV: Nguy n Tu n Anhễ ấ 5






















