
BÁO CÁO K T QU Ế Ả NGHIÊN C U Ứ, NG D NỨ Ụ G SÁNG KI N Ế
TÊN Đ TÀI:Ề H NG D N H C SINH ÔN T P PH N BÀI T P HAYƯỚ Ẫ Ọ Ậ Ầ Ậ
KHÓ TRONG CH NG 2 TÍNH QUY LU T C A HI NƯƠ Ậ Ủ Ệ
T NG DI TRUY NƯỢ Ề CHO H C SINH L P 12 TR NGỌ Ớ ƯỜ
CHO H C SINH L P 12 TR NGỌ Ớ ƯỜ
THPT BÌNH XUYÊN.
THPT BÌNH XUYÊN.
NG I NGHIÊN C U: ƯỜ Ứ Vũ Th Lanị
ĐN V : Ơ Ị TR NG THPT BÌNH XUYÊNƯỜ
1.Tóm t tắ
Trong vài năm g n đây vi c đánh giá h c sinh đc thay đi theo h ngầ ệ ọ ượ ổ ướ
tr c nghi m khách quan, trong đóắ ệ thêi lîng ph©n bè cho viÖc hoµn thµnh
mét c©u tr¾c nghiÖm khi kiÓm tra, thi lµ rÊt ng¾n (chØ cã 1,5
phót/c©u- đi v i thi T t nghi p THPT và 1,8 phút/ câu- đi v i thi tuy nố ớ ố ệ ố ớ ể
sinh Đi h c, Cao đng).Vì v y vi c thay đi ph ng pháp gi ng d y phùạ ọ ẳ ậ ệ ổ ươ ả ạ
h p v i ph ng pháp ki m tra đánh giá là r t c n thi t và quan tr ng.ợ ớ ươ ể ấ ầ ế ọ
Trong th c t gi ng d y ôn thi Đi h c, Cao đng tôi nh n th y có r tự ế ả ạ ạ ọ ẳ ậ ấ ấ
nhi u bài t p khá ph c t p, khó và m t r t nhi u th i gian n u gi i b ngề ậ ứ ạ ấ ấ ề ờ ế ả ằ
ph ng pháp thông th ng, nh ng l i tr nên đn gi n, d hi u, m t ít th iươ ườ ư ạ ở ơ ả ễ ể ấ ờ
gian n u chúng ta bi t v n d ng ph ng pháp m i. Đó là nh ng bài t p xácế ế ậ ụ ươ ớ ữ ậ
đnh t l ki u gen, t l ki u hình có liên quan t i hoán v gen.ị ỉ ệ ể ỉ ệ ể ớ ị V i nh ng câuớ ữ
h i liên quan t i ki u bài t p này th ng các thông tin trong đ ra r t dài doỏ ớ ể ậ ườ ề ấ
đó vi c đc bài nhanh, ch n ra nh ng d li u c n và nh m t s công th cệ ọ ọ ữ ữ ệ ầ ớ ộ ố ứ
c b n đ v n d ng gi i nhanh và chính xác là r t quan tr ng.ơ ả ể ậ ụ ả ấ ọ
Xu t phát t nh ng nhu c u đó c a các em h c sinh. Qua quá trình gi ngấ ừ ữ ầ ủ ọ ả
d y tôi nh n th y ph ng pháp: ạ ậ ấ ươ "Tính nhanh t l ki u hình trong các bàiỉ ệ ể
toán thu c quy lu t di truy n có x y ra hoán v genộ ậ ề ả ị cho h c sinh l p 12ọ ớ
tr ng THPT Bình xuyênườ " đã đem l i nh ng hi u qu nh t đnh. Vì v y tôiạ ữ ệ ả ấ ị ậ
m nh d n đa ra đ tài này đ các đng nghi p cùng tham kh o.ạ ạ ư ề ể ồ ệ ả
2. Gi i thi uớ ệ
- Giúp h c sinh làm đc các bài t p tr c nghi m nhanh h n, chính xác h nọ ượ ậ ắ ệ ơ ơ
t đó t o đc h ng thú cho h c sinh v i môn h c .ừ ạ ượ ứ ọ ớ ọ
Gi i pháp thay th ả ế
- Góp ph n cùng v i đng nghi p tìm ra ph ng pháp gi ng d y m i, sángầ ớ ồ ệ ươ ả ạ ớ
t o.ạ
1

- Nh m trau d i và nâng cao chuyên môn, nghi p v c a b n thân.ằ ồ ệ ụ ủ ả
V n đ nghiên c uấ ề ứ
"Tính nhanh t l ki u hình trong các bài toán thu c quy lu t di truy n có x yỉ ệ ể ộ ậ ề ả
ra hoán v genị cho h c sinh l p 12 tr ng THPT Bình xuyênọ ớ ườ " Có th c hi nự ệ
đc hay không ?ượ
Gi thuy t nghiên c u ả ế ứ
Tính nhanh t l ki u hình trong các bài toán thu c quy lu t di truy n có x yỉ ệ ể ộ ậ ề ả
ra hoán v genị cho h c sinh l p 12 tr ng THPT Bình xuyênọ ớ ườ
3.Ph ng pháp ươ
A.Khách th nghiên c u ể ứ
Đ tài đc th c hi n v i n i dung ch y u là nh ng bài t p liên quan t iề ượ ự ệ ớ ộ ủ ế ữ ậ ớ
hoán v gen trong cáị Tôi ch n tr ng THPT Bình Xuyên vì tr ng có nh ngọ ườ ườ ữ
đi u ki n thu n l i cho vi c NCKHSP D:ề ệ ậ ợ ệ Ư
- Giáo viên: Ng i th c hi n nghiên c u là ng i tr c ti p gi ng d y đã cóườ ự ệ ứ ườ ự ế ả ạ
kinh nghi m, có lòng nhi t tình, trách nhi m cao.ệ ệ ệ
- Vũ Th Lanị - Giáo viên d y l p 12Aạ ớ 1 – L p th c nghi m ớ ự ệ
- Vũ Th Lanị - Giáo viên d y l p 12Aạ ớ 3– L p đi ch ngớ ố ứ
c đ thi Đi hoc, Cao đng.ề ạ ẳ
Đi t ng : 2 nhóm h c sinh kh i 12 (m i nhóm 25 em thu c đi t ngố ượ ọ ố ỗ ộ ố ượ
h c sinh trung bình tr lên)- Tr ng THPT ọ ở ườ Bình xuyên
Th i gian th c hi n đ tài: h c kì I năm h c 201ờ ự ệ ề ọ ọ 6-2017.
Ph ng pháp nghiên c u.ươ ứ
C 2 nhóm đi t ng đu đc ti n hành 2 l n ki m tra trong th i gian 30ả ố ượ ề ượ ế ầ ể ờ
phút v i 10 bài t p.ớ ậ
L n 1: Khi ch a h ng d n h c sinh ph ng pháp tính nhanh.ầ ư ướ ẫ ọ ươ
L n 2: Sau khi đã h ng d n h c sinh làm theo ph ng pháp tính nhanh.ầ ướ ẫ ọ ươ
Quy trình nghiên c u ứ
C S KHOA H C C A HOÁN V GENƠ Ở Ọ Ủ Ị
C s di truy n:ơ ở ề
2
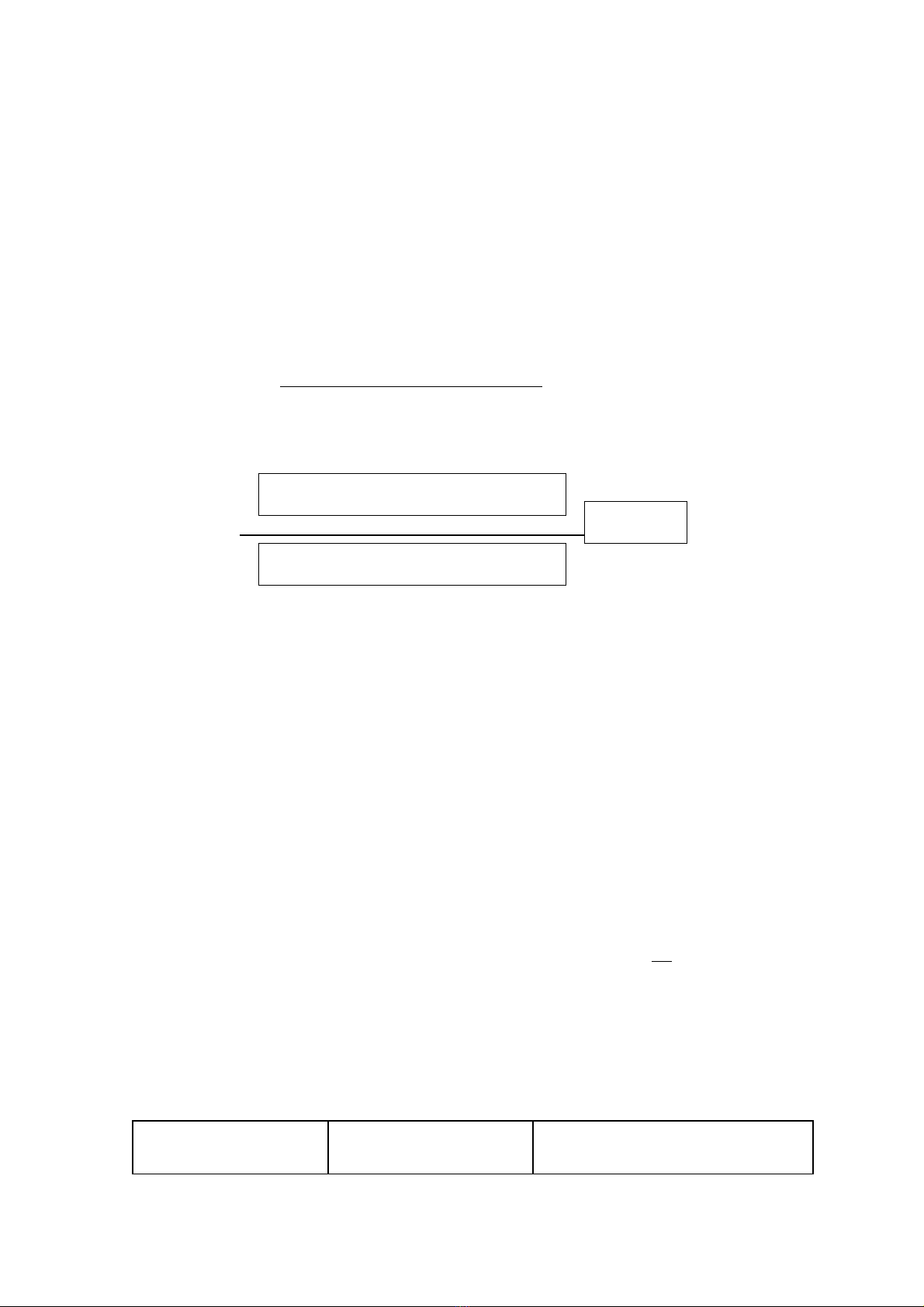
- kì đu gi m phân I, có hi n t ng ti p h p và trao đi chéo gi a 2Ở ầ ả ệ ượ ế ợ ổ ữ
trong 4 crômatit c a c p nhi m s c th kép d n t i các alen trên cùng m tủ ặ ễ ắ ể ẫ ớ ộ
nhi m s c th có th trao đi v trí cho nhau( trao đi chéo hoán v gen).→ễ ắ ể ể ổ ị ổ ị
- Vì hi n t ng trao đi chéo ch x y ra gi a 2 trong 4 crômatit, xu h ngệ ượ ổ ỉ ả ữ ướ
các gen ch y u là liên k t hoàn toàn vì v y t n s hoán v gen (f) nh h nủ ế ế ậ ầ ố ị ỏ ơ
50%.
Công th c tính t n s hoán v gen (f) ứ ầ ố ị
- Có th tính t n s hoán v gen b ng m t trong các công th c sau:ể ầ ố ị ằ ộ ứ
a. f =
b. f =
c. f = t ng t l 2 lo i giao t mang gen hoán v .ổ ỉ ệ ạ ử ị
Kho ng cách t ng đi gi a các gen trên cùng m t nhi m s c thả ươ ố ữ ộ ễ ắ ể
-T n s hoán v gen (f) th hi n l c liên k t gi a các gen trên m t nhi mầ ố ị ể ệ ự ế ữ ộ ễ
s c th (NST).ắ ể
-T n s hoán v gen th hi n kho ng cách t ng đi gi a các gen trên m tầ ố ị ể ệ ả ươ ố ữ ộ
NST, các gen n m càng xa nhau thì t n s hoán v gen càng l n và ng c l i.ằ ầ ố ị ớ ượ ạ
- D a vào (f) xác đnh v trí t ng đi trong các gen liên k t.→ự ị ị ươ ố ế
Quy c: 1 centiMoocgan(1cM) = 1% hoán v gen.ướ ị
Đa s các bài toán v hoán v gen, khi tính t n s hoán v gen, tính t lố ề ị ầ ố ị ỉ ệ
ki u hình đi con đuể ở ờ ề d a vào t l ki u hình l n ( ự ỉ ệ ể ặ
ab
ab
).
. S lo i giao t và thành ph n gen trong giao t khi các gen liên k tố ạ ử ầ ử ế
Tr ng thái genạLiên k t hoàn toànếHoán v gen (liên k t khôngị ế
hoàn toàn)
3
x 100%
S giao t có hoán v genố ử ị
T ng s giao t t o ra ổ ố ử ạ
rrthành
S cá th có ki u hình do HVGố ể ể
x 100%
T ng s cá th thu đcổ ố ể ượ
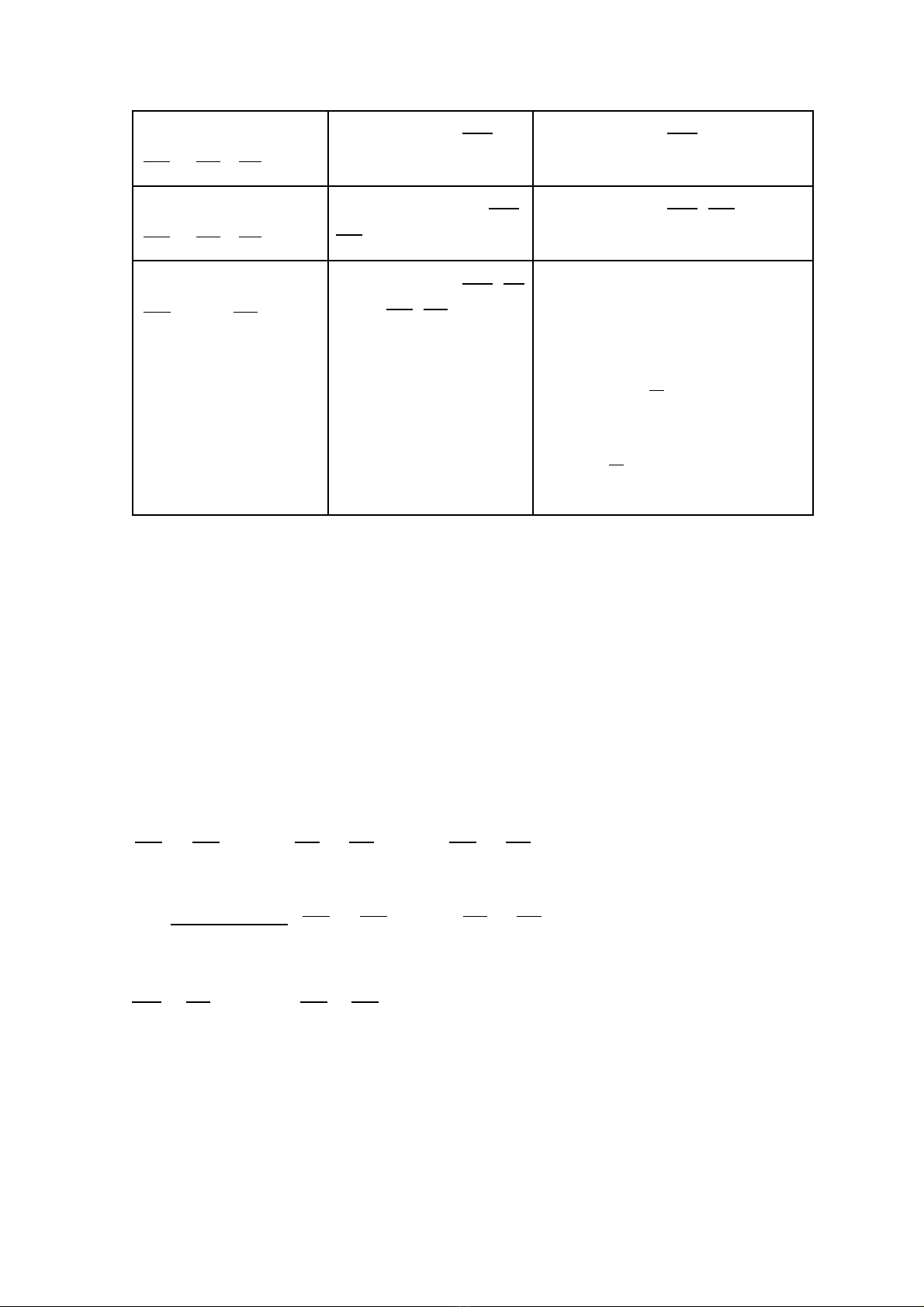
2 c p genặ đng h pồ ợ
AB
AB
; (
Ab
Ab
;
aB
aB
; ...)
1 lo i giao t ạ ử AB 1 lo i giao t ạ ử AB
1 c p gen d h pặ ị ợ
AB
Ab
; (
Ab
ab
;
aB
ab
;...)
2 lo i giao t ạ ử AB,
Ab
2 lo i giao t ạ ử AB, Ab
2 c p gen d h pặ ị ợ
ab
AB
ho c ặ
aB
Ab
2 lo i giao t ạ ử AB, ab
ho c ặAb, aB.
4 lo i giao t , t l m i lo iạ ử ỉ ệ ỗ ạ
giao t ph thu c vào t n sử ụ ộ ầ ố
HVG (f); f ≤ 50% trong đó:
+ 2 lo i giao t liên k t (t lạ ử ế ỉ ệ
l n) = 0,5 - ớ
2
f
≥ 0,25.
+ 2 lo i giao t hoán v ( t lạ ử ị ỉ ệ
nh ) = ỏ
2
f
≤ 0,25.
PH NG PHÁP XÁC ĐNH NHANH T L PHÂN LI KI U GENƯƠ Ị Ỉ Ệ Ể
VÀ KI U HÌNH CON LAI.Ể Ở
1.Tr ng h p hoán v gen x y ra c b và mườ ợ ị ả ở ả ố ẹ
Gi¶ sö thÕ hÖ ®em lai ®Òu cã hai cÆp gen dÞ hîp lµ Aa vµ Bb cïng
n»m trªn mét cÆp NST thêng ta sÏ cã c¸c trêng hîp vÒ kiÓu gen ë thÕ
hÖ xuÊt ph¸t lµ:
ab
AB
x
ab
AB
hoÆc
aB
Ab
x
aB
Ab
hoÆc
ab
AB
x
aB
Ab
.
1.1. Tr êng hîp 1 :
ab
AB
x
ab
AB
hoÆc
aB
Ab
x
aB
Ab
.
- Gi¶ sö c¸c c¬ thÓ trªn ®Òu cho 4 lo¹i giao tö víi tû lÖ lµ:
AB = ab = x% vµ Ab = aB = y%.
- D a vào t l giao t c a (P) ta l p đc b ng sau:ự ỉ ệ ử ủ ậ ượ ả
4
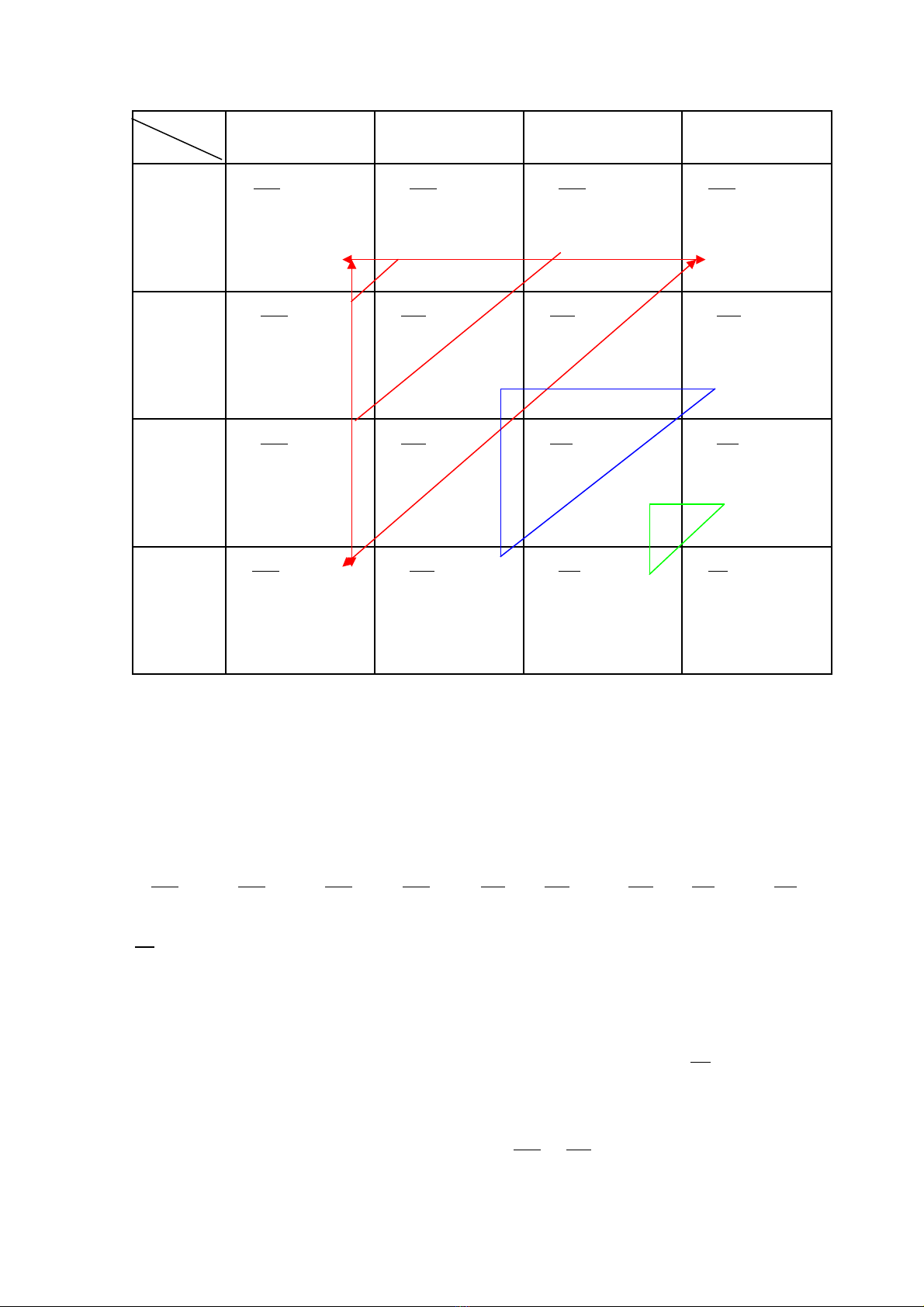
AB( x) Ab(y) aB(y) ab(x)
AB(x) x2
AB
AB
Tr i- tr iộ ộ
xy
Ab
AB
Tr i- tr iộ ộ
xy
aB
AB
Tr i- tr iộ ộ
x2
ab
AB
Tr i- tr iộ ộ
Ab(y) xy
Ab
AB
Tr i- tr iộ ộ
y2
Ab
Ab
Tr i - l nộ ặ
y2
aB
Ab
Tr i- tr iộ ộ
xy
ab
Ab
Tr i - l nộ ặ
aB(y) xy
aB
AB
Tr i- tr iộ ộ
y2
aB
Ab
Tr i- tr iộ ộ
y2
aB
aB
L n - tr iặ ộ
xy
ab
aB
L n - tr iặ ộ
ab(x) x2
ab
AB
Tr i- tr iộ ộ
xy
ab
Ab
Tr i - l nộ ặ
xy
ab
aB
L n - tr iặ ộ
x2
ab
ab
L n - l nặ ặ
T l phân li ki u gen c a ỉ ệ ể ủ F1:
Xác đnh t l phân li ki u gen c a ị ỉ ệ ể ủ F1 d a vào ựcác hình tam giác (nh b ngư ả
trên) t c là ứtheo quy luËt b¾t ®Çu tõ kiÓu gen toµn c¸c gen tréi, sau
®ã gi¶m dÇn sè gen tréi vµ t¨ng dÇn sè gen lÆn trong kiÓu gen.
x2
AB
AB
: 2xy
Ab
AB
: 2xy
aB
AB
: 2x2
ab
AB
: 2y2
aB
Ab
: y2
Ab
Ab
: 2xy
ab
Ab
: y2
aB
aB
: 2xy
ab
aB
: x2
ab
ab
.
Tỉ lÖ ph©n li kiÓu h×nh c aủ F1 :
- T l ki u hình mang 2 tính tr ng l n ( ỉ ệ ể ạ ặ
ab
ab
) = x2.
(1).
- T l ki u hình mang 2 tính tr ng tr iỉ ệ ể ạ ộ (
AB
+
aB
Ab
) = 3x2 + 4xy + 2y2.
5



















