
-1-
SÁNG KIẾN KINH NGHIỆM:
“ KHAI THÁC SÁNG TẠO,
LINH HOẠT MỘT BÀI TOÁN
SÁCH GIÁO KHOA – HÌNH
HỌC 7 ”

-2-
Chủ đề
“ KHAI THÁC SÁNG TẠO, LINH HOẠT MỘT BÀI TOÁN
SÁCH GIÁO KHOA – HÌNH HỌC 7 ”
----------------------------------
PHẦN I: MỞ ĐẦU
I. LÝ DO CHỌN ĐỀ TÀI.
Trong bối cảnh ngành Giáo dục và Đào tạo đang nỗ lực đổi mới phương pháp
dạy học theo hường phát huy tính tích cực chủ động của học sinh trong hoạt động
học tập, để dáp ứng được những đòi hỏi được đặt ra cho sự bùng nổ kiến thức và
sáng tạo kiến thức mới, cần phải phát triển năng lực tư duy, năng lực giải quyết vấn
đề và tính sáng tạo.
Hướng giải quyết hiện nay là tích cực hoá hoạt động học tập của học sinh, khơi
dậy và phát triển năng lực tự học nhằm hình thành cho học sinh tư duy tích cực,
độc lập sáng tạo, nâng cao năng lực phát hiện và giải quyết vấn đề, rèn luyện kỹ
năng vận dụng kiến thức vào thực tiễn, tác động đến tình cảm, đem lại niềm tin,
hứng thú học tập cho học sinh.
Dạy toán thực chất là dạy hoạt động toán, học sinh cần phải đước cuốn hút vào
những hoạt động học tập do giáo viên tổ chức chỉ đạo, thông qua đó học sinh tự lực
khám phá những điều mình chưa biết chứ không phải thụ động tiếp thu những tri
thức đã sắp đặt sẵn.
Theo tinh thần này, trong tiết lên lớp tôi luôn tổ chức chỉ đạo học sinh tiến hành
các hoạt động học tập: Củng cố kiến thức cũ, tìm tòi phát hiện những kiến thức
mới, luyện tập vận dụng kiến thức vào những tình huống khác nhau. Không những
thế, tôi luôn suy nghĩ làm thế nào để học sinh có thể tự đọc hiểu được tào liệu, tự
làm bài tập, nắm vững và hiểu sâu các kiến thức cơ bản, đồng thời phát huy tiềm
năng sáng tạo của bản thân.
Do vậy, tôi đã tìm tòi, học hỏi đồng nghiệp, tham khảo tài liệu để viết đề tài này
nhằm hướng dẫn học sinh biết khai thác sáng tạo các bài toàn đơn giản trong sách
giáo khoa thành các bài toán mới đa dạng, có đơn giản, có phức tạp, giúp học sinh
tự phân tích, tổng hợp, đặc biệt hoá, khái quát hoá, tương tự, quy lạ về quen, quy
khó về dễ, để từ đó giúp học sinh hứng thú hơn trong học toán.

-3-
II. MỤC ĐÍCH NGHIÊN CỨU:
- Khai thác sáng tạo, linh hoạt từ một bài toán hình học ở sách giáo khoa toán
7 thành những bài toán khác phù hợp với từng đối tượng học sinh.
- Phát huy tư duy tích cực, độc lập sáng tạo, nâng cao năng lực phát hiện và
giải quyết vấn đề, rèn luyện kỹ năng vận dụng kiến thức vào thực tiễn của
học sinh.
- Giúp giáo viên có tư liệu tham khảo về vấn đề này.
III. NHIỆM VỤ NGHIÊN CỨU:
- Nghiên cứu về tình hình dạy và học vấn đề này ở trường.
- Đưa ra được một số bài toán phù hợp với đối tượng học sinh và hướng giải
quyết.
IV. PHẠM VI NGHIÊN CỨU:
1. Đối tượng nghiên cứu:
- Các tài liệu.
- Giáo viên, học sinh lớp 7 trường THCS Viên Thành
2. Phạm vi nghiên cứu:
Các bài toán hình học phù hợp với đối tượng học sinh lớp 7, phương pháp
giải các bài toán đó.
V. PHƯƠNG PHÁP NGHIÊN CỨU:
- Phương pháp nghiên cứu tài liệu.
- Phương pháp điều tra khảo sát
- Phương pháp thể nghiệm.
- Phương pháp tổng kết kinh nghiệm.
PHẦN II: NỘI DUNG
-4-
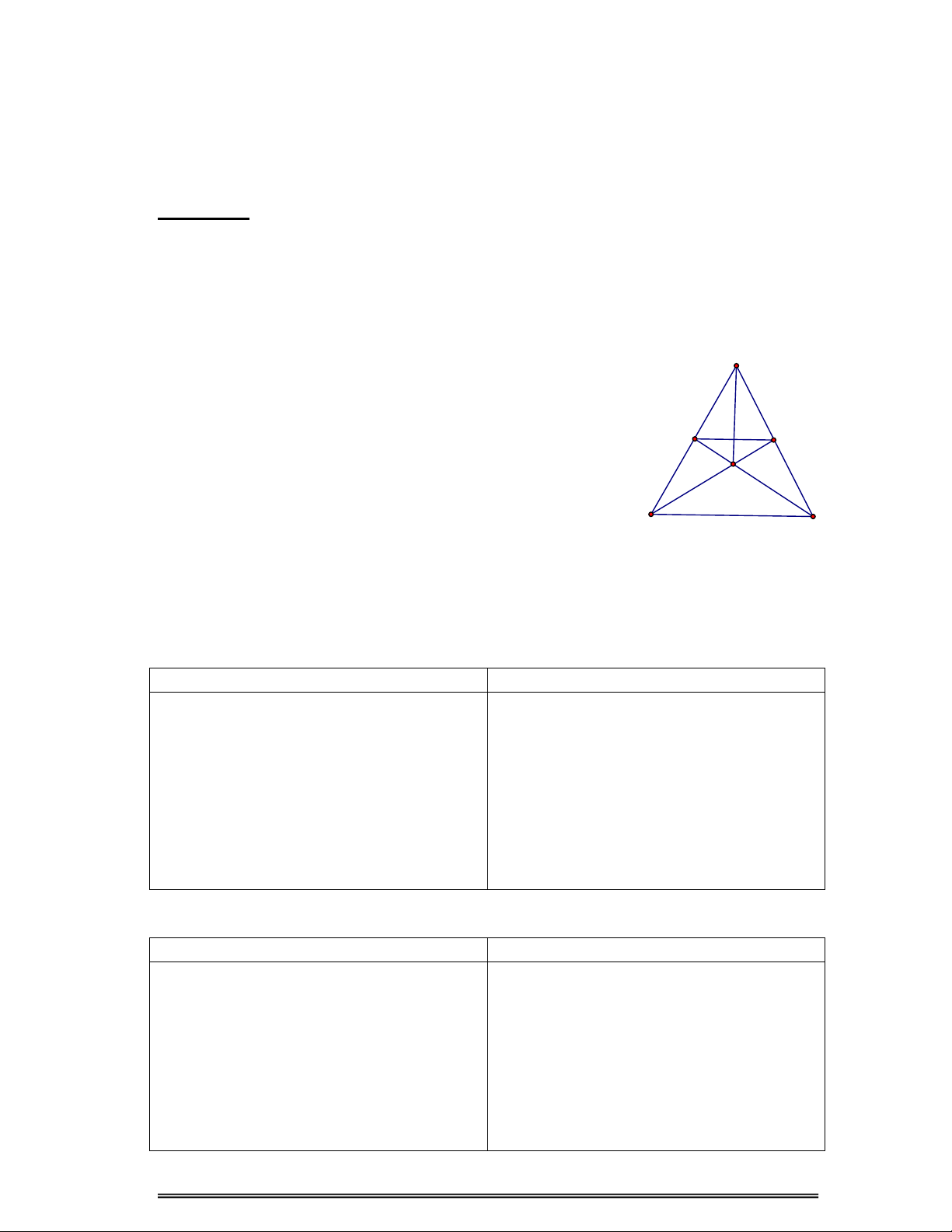
Từ bài toán sách giáo khoa toán 7:
( Bài 65 – trang 137 – SGK – Toán 7 – Tập 1 – NXB giáo dục 2003)
Bài toán I : Cho
ABC
cân tại A ( Â < 900 ), Vẽ
BH AC
( H
AC ), CK
AB ( K
AB ).
a. Chứng minh rằng AH = AK.
b. Gọi I là giao điểm của BH và CK. Chứng minh rằng AI là tia phân giác
của góc A.
Phân tích bài toán I:
- Để chứng minh hai đoạn thẳng hay hai góc bằng
nhau, thông thường ta phải chứng minh hai tam
giác chứa hai đoạn thẳng hoặc hai góc đó bằng
nhau ( Tuy nhiên còn nhiều cách khác). Vậy để
chứng minh AH = AK ta phải chứng minh 2 tam
giác nào bằng nhau?
- Hai tam giác đó bằng nhau theo trường hợp nào?
Giả thiết đã cho ta được gì rồi? Có thể chứng
minh hai đoạn thẳng đó bằng nhau trực tiếp
không? Hay phải thông qua các yếu tố trung gian
nào?
Bằng các câu hỏi gợi mở, giáo viên để học sinh thảo luận rồi đưa ra phương án
chứng minh riêng của học sinh.
Giáo viên có thể hướng đẫn cho học sinh theo một trong 2 sơ đồ sau:
Sơ đồ 1 Sơ đồ 2
AH = AK
ABH ACK
AB = AC (
ABC
cân);
KAH
chung
AH = AK
BK = CK ( Vì AB = AC)
KCB HBC
BC chung;
KCB
=
HCB
(
ABC
cân)
- Tương tự như trên giáo viên nêu hệ thống câu hỏi gợi mở giúp học sinh tìm ra
được lời giải câu b theo một trong các sơ đồ sau:
Sơ đồ 1 Sơ đồ 2
AI là phân giác của góc A
Â1= Â2
AKI AHI
AK = AH ( c/m ở câu a); AI chung
AI là phân giác của góc A
Â1= Â2
ABI ACI
+B1= B2 (
KBC HCB
+AB = AC (
ABC
cân tại A)
2
1
2
1
2
1
H×nh 1
I
C
B
A
KH
-5-
+ AI cạnh chung
ở bài toán A ( hình 1), ta đã chứng minh được AK = AH và
AKH
là tam giác cân ở
A; do vậy học sinh tính được
0
180
2
BAC
AKH AHK
(1)
Và giả thiết cho
ABC
cân tại A nên học sinh chứng minh được:
0
180
2
BAC
BAC ABC
(2)
Từ (1) và (2) suy ra:
AKH ABC
, mà 2 góc này ở vị trí đồng vị,điều này giúp học
sinh chứng minh được: KH // BC.
Vậy ta có bài toán sau:
Bài toán 1: Cho
ABC
cân ở A ( Â < 900), Vẽ
BH AC
( H
AC ), K
AB (
K
AB ). Chứng minh rằng: KH // BC.
ở bài toán A ( hình 2),
ABC
cân ở A
AB = AC, học sinh đã chứng minh được Â1 = Â2, có
thêm AN là cạnh chung nên suy ra:
ABN ACN
(c.g.c)
1 2
N N
mà
0
1 2
180
N N ( kề bù)
0
0
1 2
180
90
2
N N
AN BC
hay
AI BC
Từ đó giúp học sinh chứng minh được bài toán sau:
Bài toán 2: Cho
ABC
cân ở A ( Â < 900), có các đường cao hạ từ đỉnh B và
đỉnh C cắt nhau tại I. Chứng minh rằng:
AI BC
.
Vì học sinh đã chứng minh được KH // BC ( như bài toán 1), mà bài toán 2 lại
chứng minh được
AI BC
, nên ta cũng chứng minh được AI
KH.
Từ đó giúp học sinh dễ dàng chứng minh được bài toán sau:
Bài toán 3: Cho
ABC
cân ở A ( Â < 900), có các đường cao hạ từ đỉnh B và
đỉnh C cắt nhau tại I. Chứng minh rằng: AI
KH.
Như đã chứng minh ở bài toán 2 (hình 2):
ABN ACN
(c.g.c)
BN CN
N là trung điểm của BC.
Từ đó giúp học sinh tìm được lời giải cho bài toán sau:
Bài toán 4: Cho
ABC
cân ở A ( Â < 900), có các đường cao hạ từ đỉnh B và
đỉnh C cắt nhau tại I. Chứng minh rằng:AI đi qua trung điểm của BC.
Bài toán khác tương tự:
Bài toán 5: Cho
ABC
cân ở A ( Â < 900), có các đường cao BH, CK ( H
AC,
K
AB ) cắt nhau tại I.
Chứng minh rằng:AI đi qua trung điểm của KH.
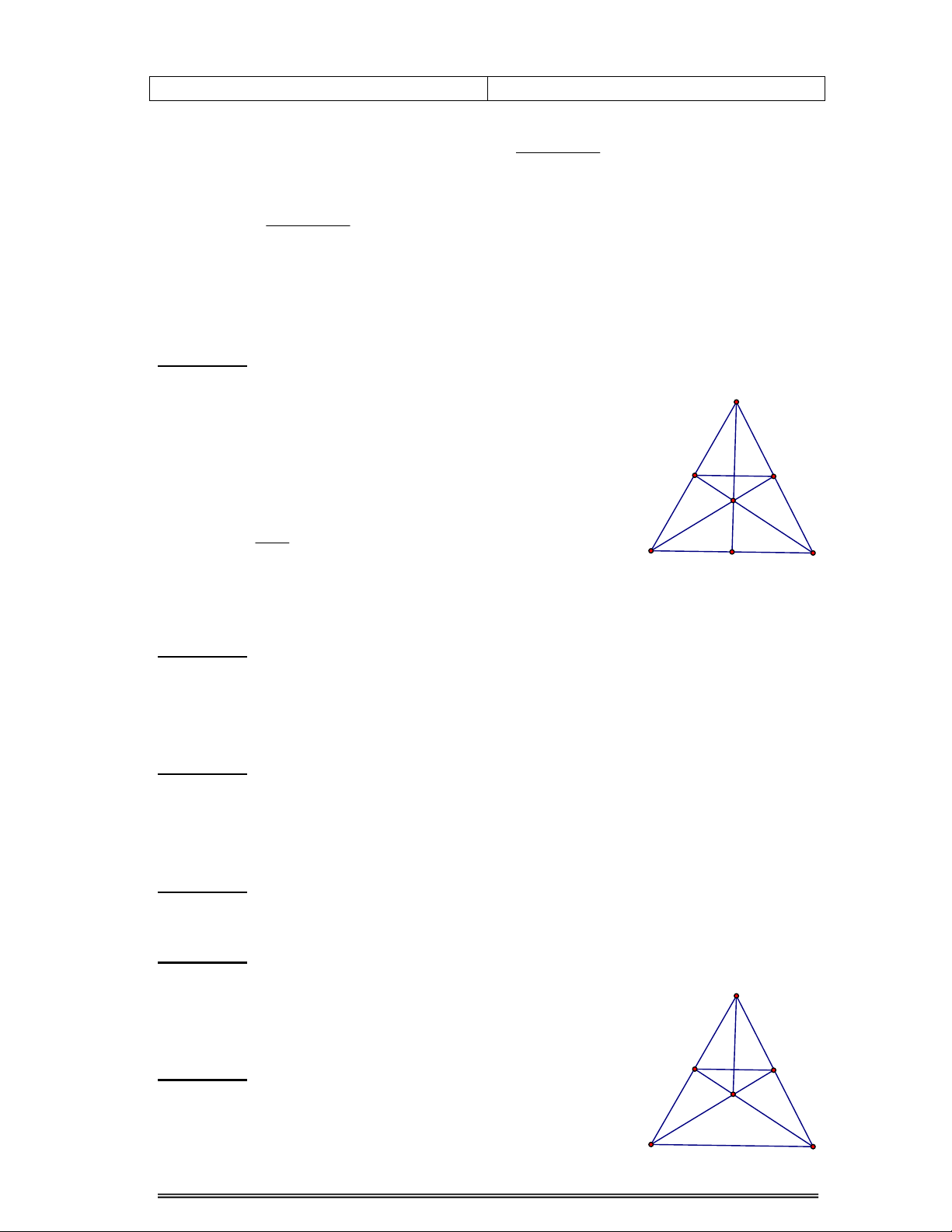
Tổng hợp các bài toán trên ( hình 3), học sinh chứng
minh được các bài toán tương tự sau:
Bài toán 6: Cho
ABC
cân ở A ( Â < 900), có các
đường cao hạ từ đỉnh B và đỉnh C cắt nhau tại I.
Chứng minh rằng: AI vừa là đường phân giác, vừa là
đường cao, vừa là đường trung tuyến, vừa là đường
2
1
2
1
2
1
H×nh 2
I
C
B
A
KH
2
1
H×nh 3
I
C
B
A
KH


























