Summary of Engineering doctoral dissertation: Proposed optimal control algorithms for photovoltaic arrays reconfiguration

Chia sẻ: _ _ | Ngày: | Loại File: PDF | Số trang:26

Thêm vào BST

Báo xấu

24
lượt xem 4
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Thesis objectives and tasks: Establishing a mathematical model, putting forward an algorithm applied for seeking the solar system's irradiance equalization configuration under the heterogeneous lighting conditions; establishing a mathematical model, putting forward an algorithm applied for choosing an optimal circuit switching method, from the initial connection configuration to the irradiance equalization configuration.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Summary of Engineering doctoral dissertation: Proposed optimal control algorithms for photovoltaic arrays reconfiguration

MINISTRY OF EDUCATION VIETNAM ACADEMY OF SCIENCE AND TRAINING AND TECHNOLOGY GRADUATE UNIVERSITY OF SCIENCE AND TECHNOLOGY ----------------------------- Ngo Ngoc Thanh PROPOSED OPTIMAL CONTROL ALGORITHMS FOR PHOTOVOLTAIC ARRAYS RECONFIGURATION Major: Control and Automation Technology Code: 9.52.02.16 SUMMARY OF ENGINEERING DOCTORAL DISSERTATION Ha Noi – 2020
This work is completed at: Graduate University of Science and Technology Vietnam Academy of Science and Technology Supervisor: Assoc.Prof.Dr. Pham Thuong Cat Prof.Dr. Nguyen Phung Quang Reviewer 1: ……………………………………………………..........................………. ……………………………………………………………………………........................ Reviewer 2: ………………………………………………………………........................ …………………………………………………………………………............................ Reviewer 3: ………………………………………………………………........................ ……………………………………………………………………………........................ This Dissertation will be officially presented in front of the Doctoral Dissertation Grading Committee, meeting at: Graduate University of Science and Technology Vietnam Academy of Science and Technology At …………. hrs ……. day ……. month……. year ……. This Dissertation is available at: 1. Library of Graduate University of Science and Technology 2. National Library of Vietnam
INTRODUCTION 1. Introduction Photovoltaic panels during the working process in solar power plants can receive inconsistent solar irradiance levels in many cases due to the partial shading. In the context of partial shading, the system capacity shows a significant decrease, in addition to the phenomenon of Misleading (confusion due to the maximum power point). Development of a solar system reconfiguration strategy based on the irradiance equalization method is a key area of research, whereby the solar system restructuring is the rearrangement of the connection circuitry of photovoltaic panels for the purposes of increased output power and device protection when the solar system works in heterogeneous lighting conditions. Therefore, the topic “Proposed optimal control algorithms for photovoltaic arrays reconfiguration” was selected for this thesis to contribute to solving problems in the solar system reconfiguration strategy. 2. Thesis objectives and tasks ✓ Establishing a mathematical model, putting forward an algorithm applied for seeking the solar system's irradiance equalization configuration under the heterogeneous lighting conditions. ✓ Establishing a mathematical model, putting forward an algorithm applied for choosing an optimal circuit switching method, from the initial connection configuration to the irradiance equalization configuration. 3. Research scope ✓ Studying primary sources, connecting photovoltaic panels with the use of TCT connection circuit. ✓ Without considering constraints on equipment production costs, economic nature when putting into practice. 4. New findings of the thesis ✓ Establishing the mathematical model, applying Dynamic programming (DP) algorithm and proposing Smartchoice (SC) algorithm for selecting the irradiance equalization configuration to find ways of arranging connection positions of photovoltaic panels so that optimal system power and local maximum points elimination can be achieved. ✓ Proposing the mathematical model, applying the Munkres assignment algorithm (MAA) and proposing an improved MAA for selecting the optimal circuit switching method aimed at extending the life of switching matrix in the solar system. ✓ Building a simulation toolkit on Matlab-Simulink and Micrsoft Visual Studio in order to assess the performance and accuracy of algorithms used for proving new methods of the thesis. 5. Thesis structure: The thesis is broken down into 4 chapters. Chapter 1: Solar system structure and system performance improvement strategy under partial shading conditions. Chapter 2: Introduction to the optimal control theory Chapter 3: Development of a system restructuring strategy using optimal control theory Chapter 4: Simulation and experiment 1
Chapter 1: SOLAR SYSTEM STRUCTURE AND SYSTEM PERFORMANCE IMPROVEMENT STRATEGY UNDER PARTIAL SHADING CONDITIONS. 1.1 Introduction to the solar system 1.1.3 Solar power Solar power is generated from either the conversion of sunlight into electricity, or directly by using photovoltaic panels, or indirectly through thermal energy using the concentrated solar power. 1.1.4 Photovoltaic panels connecting structures There are basically two main connection standards for photovoltaic panels: serial and parallel. The advantage and disadvantage of parallel connection circuit are that the current is the total current of photovoltaic panels, and the voltage is equal to the minimum voltage of photovoltaic panels, respectively. The advantage and disadvantage of serial connection circuit are that the voltage is the total voltage of photovoltaic panels, and the current is equal to the minimum current of photovoltaic panels, respectively. Figure 1-13 shows 6 different connection methods of photovoltaic panels commonly used. Although there are many special connection structures with lots of advantages being studied and applied, the most commonly exploited solution currently in practice is SP connection circuit as Figure 1-13c and TCT connection circuit as Figure 1-13d. Hình 1-13. Photovoltaic panel connection circuits; (a) Series array; (b) Parallel array; (c) Series-Parallel array (SP); (d) Total-Cross-Tied array (TCT); (e) Bridge-Link array; (f) Honey-Comb array 1.1.5 Basic structure of grid-connected solar system with power storage There are three main parts: photovoltaic panels connection array, converters and load (local load or grid). In addition, extra batteries can be used for storage and power stabilization purposes. 1.2 Introduction to the system performance improvement strategy under partial shading conditions. 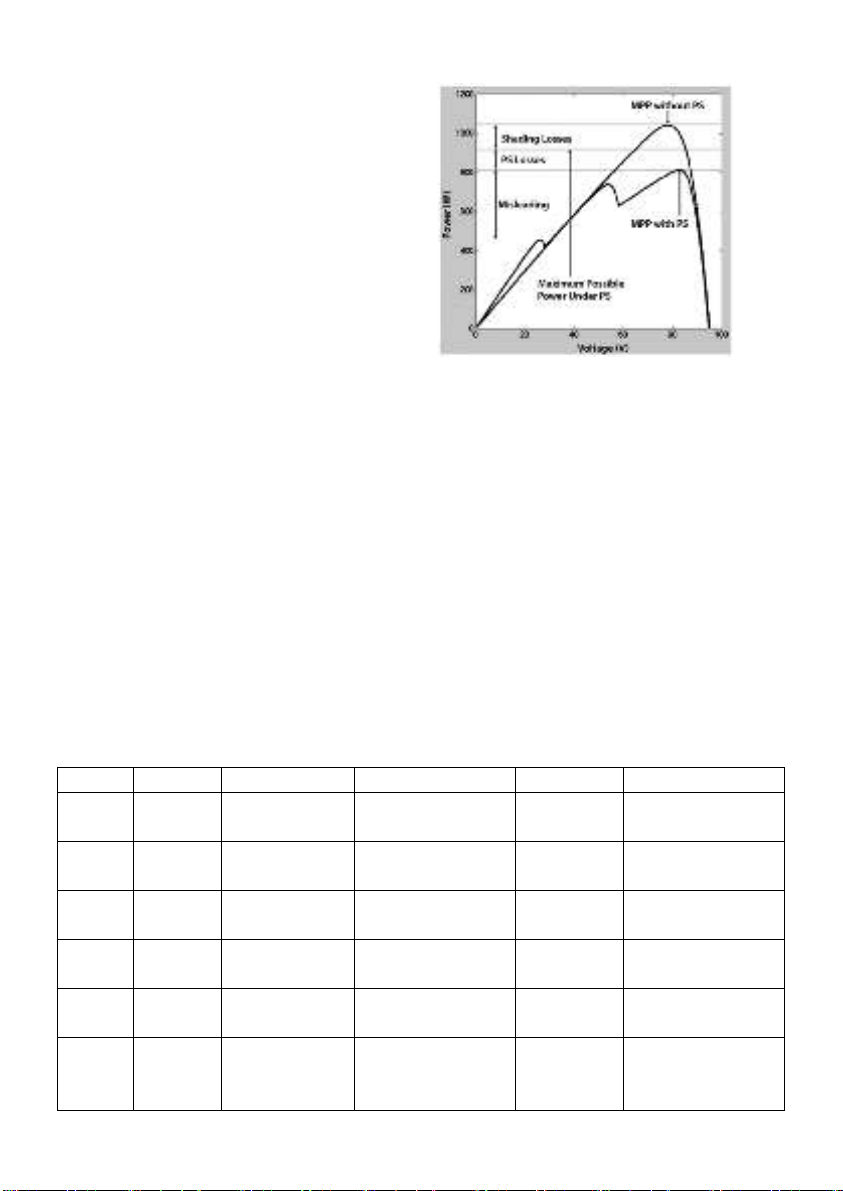1.2.1 Effects of partial shading The reduction in capacity of the solar system in the context of shading is shown in Figure 1-21. In the context of partial shading, the system capacity shows a significant decrease, in addition to the phenomenon of misleading (confusion due to the maximum power point). 2
1.2.2 Power attenuation minimization techniques due to the partial shading Currently, the studies to reduce the loss of solar energy system in the world are classified into three main groups: Distributed MPP, multi-level converter and solar system restructuring method. Photovoltaic panel circuits restructuring was first proposed by Salameh et al., used for the operation and speeding of electric vehicles using solar panels. Sherif and Boutros did propose the photovoltaic panel circuits restructuring by using Figure 1-21. Shading, partial shading, and misleading transistors and circuit breakers. losses for a photovoltaic array. Shading, partial shading, and misleading losses for a photovoltaic array. Nguyen and Lehman used the restructuring circuit inside the photovoltaic panels and proposed two optimal algorithms to control the restructuring circuit. Velasco et al. applied the restructuring method to the grid system and proposed a mathematical model for it. However, all is only at the local optimal level, instead of offering an overall optimal configuration. Velasco proposed the EI (Equalization Index), understood as the difference between the row with the highest total solar irradiance compared to the row with the lowest total solar irradiance; accordingly, the configuration with the lowest EI is known as the overall optimal configuration. The most optimal configuration requires the minimum illumination difference level received by the photovoltaic panels in each parallel circuit. 1.2.5 Comparison of methods presented The methods in the solar system restructuring strategy have different advantages and disadvantages, as shown in Table 1-9 below. Table 1-9. Comparison of irradiance equalization algorithms using TCT connection circuit Tác giả Chiến lược Thuật toán điều khiển Số khóa Yêu cầu dữ liệu Ghi chú Velasco- Irradiance - 2.NPV.m-throw current, voltage static and dynamic part Quesada equalization Irradiance Deterministic and NSW = (2.m.NPV)DPST + supports row with different Romano irradiance equalization Random search (m)SPDT number modules Irradiance supports row with different Storey Best worst sorting NSW = NPV.(m2-m)SPST current, voltage equalization number modules Matam and Irradiance Arrange in descending current, voltage, Dynamic PV array is formed 24-DPST relays Barry equalization order of radiation irradiance using PV modules Irradiance Reconfiguration supports row with different Jazayeri - irradiance equalization algorithm number modules Mahmoud Irradiance fixed part along with and El- Greedy algorithm - irradiance equalization adaptive part Saadany 3
1.3 Conclusions of Chapter 1 In Chapter 1, the author gives an overview of the grid-connected solar system including its components, model connecting such basic components and photovoltaic panel connection structures. In the next section, the author presents an overview of the solar system performance improvement strategy under heterogeneous lighting conditions for TCT connection circuit and SP connection circuit based on the irradiance equalization method. Advantages and disadvantages of optimal algorithms in other studies, statistical table of characteristics of listed methods have been analyzed to get an overview of evaluation of the pros and cons of such methods. Chapter 2: INTRODUCTION TO THE OPTIMAL CONTROL THEORY 2.1 Introduction to the optimal control theory The optimal control is aimed to find the optimal signal u* so that the objective function Q can reach the maximum or minimum value. The most basic methods of optimal control are broken down into two main groups: static optimization control and dynamic optimization control. 2.2 Formulation of the optimal control problem 2.2.1 Control circuit structure in the solar system Although the circuit structures have very diverse forces, they all share the same characteristics of control function block diagram for the solar panels shown in Figure 2-1. Accordingly, a power electronic control system for solar panels is divided into three functional levels. Figure 2-1. Block diagram of grid-connected electronic power control function for solar panels. The research objective of this thesis is to propose a photovoltaic panel connection restructuring method enabling the system always work with the highest efficiency. Photovoltaic panel connection restructuring is shown in Figure 2-2 (CT2). 4
1 2 n1 1 n2 2 nm m PV Reconfiguration techniques. HANOI May 2013 (a) (b) (c) Figure 2-2. Photovoltaic array reconfiguration: (a) TCT topology, (b) Dynamic electrical scheme, (c) Dynamic Figure 2-7: Connection topologies of the PV array configuration by using DES The restructuring unit is located in front of the inverter to change the photovoltaic panels connection, so the control circuit applied in the restructuring unit is under level 2 - the typical control level of solar panels. 2.2.2 Restructuring unit 14 The location of restructuring unit is shown in Figure 2-3. Reconfigura tion system Hình 2-3. Bộ tái cấu trúc trong hệ thống NLMT hòa Hình 2-4. Các thành phần trong bộ tái cấu lưới có dự trữ trúc The restructuring unit (CT1) depicted in Figure 2-4 is mainly composed of a switching matrix and a controller. Initially, the controller functioned as measuring the current, voltage of photovoltaic panels, estimating lighting levels, and finding the highest connection configuration for system capacity. Then, it ordered the opening and closing of keys in the switching matrix, switching the photovoltaic panel connection configuration from the initial configuration to the optimal configuration. 2.2.3 Proposal on the Control system In this thesis, an open control system is proposed to be applied by the PhD student in order to build a restructuring unit according to the flowchart in Figure 2-5 (CT2). Seeking the optimal Closing and opening Measurement of panels’ switching configuration of keys in the current and voltage and method switching matrix Figure 2-5. An open control system for the restructuring unit 5
2.2.4 Proposal on the optimal control method The proposed optimal control method applied in the restructuring unit as shown in Figure 2-6 (see CT2) includes 2 main problems: Seeking the irradiance equalization configuration and selecting the optimal switching method. Solar irradiance and current connection position of each photovoltaic panel are the input data of this method. The new connection position of each photovoltaic panel is the method’s outcome. Thus, this is a problem of which the model's input, output and state variables are independent of time, and the output value at a time is dependent on the input value and states at that time only. Static optimization control method is selected to apply for the two above optimization problems. Figure 2-6. Flowchart of the algorithm for the system reconfiguration 2.3 Some optimal problems used in the thesis. 2.3.1 Subset sum problem The subset sum problem was introduced by Knapsack for the first time in 1990. It is stated as follows: Given AS with a set of nAS items and a knapsack, wj being the weight of item j; c is the capacity of that knapsack. Requirements: Select a subset of the items of which the total weight is closest to, without exceeding, c 𝑛𝐴𝑆 That is, finding the maximum value of 𝑧 = ∑𝑗=1 𝑤𝑗 𝑥𝑗 satisfying the condition that 𝑛𝐴𝑆 ∑𝑗=1 𝑤𝑗 𝑥𝑗 ≤ 𝑐 with 𝑥𝑗 = 0 𝑜𝑟 1, 𝑗 ∈ 𝑁 = {1, . . , 𝑛𝐴𝑆 } 1, 𝑖𝑛 𝑐𝑎𝑠𝑒 𝑜𝑓 𝑠𝑒𝑙𝑒𝑐𝑖𝑛𝑔 𝑡ℎ𝑒 𝑖𝑡𝑒𝑚 𝑗 so that 𝑥𝑗 = { 0, 𝑖𝑛 𝑐𝑎𝑠𝑒 𝑜𝑓 𝑛𝑜𝑡 𝑠𝑒𝑙𝑒𝑐𝑖𝑛𝑔 𝑡ℎ𝑒 𝑖𝑡𝑒𝑚 𝑗 Generalize the problem with the objective function of maximum weight z: 𝑛𝐴𝑆 ( 2-8 ) maximize z = ∑ 𝑤𝑗 𝑥𝑗 𝑗=1 𝑛𝐴𝑆 Constraint: ( 2-9 ) ∑ 𝑤𝑗 𝑥𝑗 ≤ 𝑐 𝑗=1 𝑥𝑗 = 0 𝑜𝑟 1, 𝑗 ∈ 𝑁 = {1, . . , 𝑛𝐴𝑆 } { 𝑤𝑗 ≥ 0 𝑗 ∈ 𝑁 = {1, . . , 𝑛𝐴𝑆 } 6
2.3.2 Munkres' Assignment Algorithm (MAA) This is the first task division problem proposed by author James Munkres. It is stated as follows: Contents of the problem: Given nM workers (iM = 1, 2, ... , nM) and nM tasks (jM = 1, 2, ... , nM). In order to assign the worker iM to perform the task jM, cost of CiMjM ≥ 0 as required. The problem is to assign which task to which worker (each worker only performs one task; each task is performed by one worker only) to incur the lowest total cost? General C matrix in Figure 2-7: Worker Task 1 2 ... nM 1 C11 C12 𝐶1𝑛𝑀 2 C21 C22 𝐶2𝑛𝑀 ... nM 𝐶𝑛𝑀1 𝐶𝑛𝑀2 𝐶𝑛𝑀𝑛𝑀 Figure 2-7. Matrix general C The mathematical model of this problem is as follows: 𝑛𝑀 𝑛𝑀 ( 2-14 ) 𝑧𝑀 = ∑ ∑ 𝐶𝑖𝑀𝑗𝑀 𝑥𝑖𝑀𝑗𝑀 → 𝑚𝑖𝑛 𝑖𝑀=1 𝑗𝑀 =1 Provided that: 𝑛 Each worker only performs one task: ∑𝑗𝑀𝑀=1 𝑥𝑖𝑀 𝑗𝑀 = 1 , 𝑖𝑀 = 1, … , 𝑛𝑀 ( 215 ) Each task is performed by one worker only: ∑𝑛𝑖𝑀𝑀=1 𝑥𝑖𝑀𝑗𝑀 = 1 , 𝑗𝑀 = ( 216 ) 1, … , 𝑛𝑀 𝑥𝑖𝑀𝑗𝑀 = 0 ℎ𝑎𝑦 1 , 𝑖𝑀 = 1 , … , 𝑛𝑀 ; 𝑗𝑀 = 1 , … , 𝑛𝑀 ( 217 ) due to the availability of conditions (2-15) (2-16), the conditions (2-17) can be replaced with 𝑥𝑖𝑀𝑗𝑀 integer ≥0, iM = 1 , 2 , ... , nM ; jM = 1 , 2 , ... , nM ( 218 ) 2.4 Conclusions of Chapter 2 Chapter 2 provides an overview of the optimal control problem, thereby proposing the optimal control method and formulating the optimal control problem used in the thesis. The first section gives an overview of the optimal control problem, provides definitions, limiting conditions, and classification of the optimal control problem. In the next section, the author formulates an optimal control problem used in the restructuring unit. For the last section, there are two optimization problems presented as the basis for proposing the optimal algorithms for the thesis: Subset sum problem and Munkres' Assignment Algorithm. The application of optimal control in the photovoltaic panels connection restructuring problem will increase the efficiency of the solar system under lighting conditions. The static optimization problem, with the open control system, is proposed to be applied by the author to build a structure that is fast acting and applicable to large solar systems. 7
Chapter 3: DEVELOPMENT OF A SYSTEM RESTRUCTURING STRATEGY USING OPTIMAL CONTROL THEORY 3.1 Irradiance equalization strategy with TCT connection circuit Irradiance equalization method for TCT connection circuit (Figure 1-13d) is the rearrangement of photovoltaic panel connection positions in order to balance the total solar irradiance at the parallel connections in TCT circuit (CT1,5). The Irradiance equalization method, improving the efficiency of the solar system can be generalized according to the diagram in Figure 2-6. This method is designed to make the solar system always operate at the highest efficiency with repetition in a certain period of time. 3.2 Measurement of current and voltage of photovoltaic panels During operation, the photovoltaic panels are connected to each other, and their current and voltage are interdependent as analyzed in section 1.1.4. It is big challenge to measure the current and voltage exactly generated by each photovoltaic cell as a basis for estimating the solar irradiance received by each photovoltaic panel. In this thesis, the measurement method shown in Figure 3-2 (for example, the measurement circuit for 4 Figure 3-2. Current and voltage acquisition circuit photovoltaic panels) (CT9) is used. 3.3 Solar irradiance estimation After measuring the current and voltage at each photovoltaic panel, the solar irradiance calculation formula (3-1) of each photovoltaic panel is applied. 𝑉+𝐼𝑅𝑆 𝐺𝑆𝑇𝐶 𝑇 𝑉 + 𝐼𝑅𝑆 𝑛𝑆𝐴𝑑 𝑘 𝑞𝑐 𝐺𝑆 = [𝐼 + 𝐼0 (𝑒 − 1) + ] (3-1) 𝐼𝐿𝑆𝑇𝐶 + 𝜇1𝑠𝑐 (𝑇𝑐 − 𝑇𝐶 𝑆𝑇𝐶 ) 𝑅𝑆ℎ 3.4 Proposal of the mathematical model (s) and 02 algorithms for Seeking the irradiance equalization configuration The mathematical model, DP algorithm application method and SC algorithm prposal are announced in (CT8), (CT1) and (CT3), respectively. 3.4.1 Mathematical model establishment 𝑛𝑖 𝑛𝑖 (3-4) 𝐸𝐼 = max (∑ 𝐺𝑖𝑗 ) − min (∑ 𝐺𝑖𝑗 ) → 0 𝑖=1,𝑚 𝑖=1,𝑚 𝑗=1 𝑗=1 Constraints: 𝑛1 + 𝑛2 + 𝑛3 + . . . +𝑛𝑚 = 𝑛 (3-5) 𝐺𝑖1 + 𝐺𝑖2 + 𝐺𝑖3 + . . . + 𝐺𝑖𝑛𝑖 = 𝐺𝑖 𝑛𝑖 > 0 𝐺𝑖𝑗 ≥ 0 𝑖 = 1, 𝑚 ; 𝑗 = 1, 𝑛𝑖 { 8
Where: EI : Equalization index, 𝑛𝑖 : number of photovoltaic panels in row i, n : total number of photovoltaic panels, 𝐺𝑖𝑗 : irradiance of PV panels in row i, column j, m : number of rows in TCT circuit, 𝐺𝑖 : total irradiance at row i. The objective function (3-4) is aimed at selecting a configuration with the smallest irradiance difference in the rows, that is, the difference between the row with the highest total solar irradiance and the row with the lowest total solar irradiance, whereby an EI of 0 is ideal. 3.4.2 Application of Dynamic programming algorithm (CT1) 3.4.2.1. Application method Considering the general TCT connection circuit in Figure 2-c. The system consists of m rows subject to serial connection. The row i consists of ni photovoltaic panels subject to parallel connection. Solar irradiance given by each photovoltaic cell is Gij with i, j being the row and column index of the photovoltaic panel placement, respectively. 𝑛𝑖 Total solar irradiance received at row i: 𝐺𝑖 = ∑𝑗=1 𝐺𝑖𝑗 (3-2) Total number of photovoltaic panels: 𝑔 = ∑𝑚 𝑖=1 𝑛𝑖 (3-6) The number of rows of the solar system m, after seeking the optimal connection configuration, may differ from the number of rows k (of the initial structure), depending on the calculation of input voltage range for the structuring unit. The total solar irradiance per row in the ideal optimal connection configuration is equal to the average of the total solar ∑𝑚 𝑖=1 𝐺𝑖 irradiance at all photovoltaic panels divided by rows:: 𝑎𝑣𝑔 = (3-7) 𝑚 The method applied is shown in the flowchart of Figure 3-4. Based on results of Dynamic Programming algorithm for the Subset sum problem, it can be noticed at each step that: 𝑛_𝑜𝑝𝑖 (3-8) 𝐺_𝑂𝑃𝑖 = ∑ 𝐺_𝑂𝑃𝑖𝑗 → 𝑎𝑣𝑔 𝑗=1 Infer: 𝐸𝐼 (3-9) = max (𝐺_𝑂𝑃𝑖 ) 𝑖=1,𝑚 − min (𝐺_𝑂𝑃𝑖 ) → 0 𝑖=1,𝑚 G_OP is the optimal connection and irradiance equalization configuration that Figure 3-4. Flowchart of the method of applying the satisfies the objective function (3-4) presented Dynamic Programming in the problem of finding in section 3.4.1. Irradiance Equalization 9
3.4.2.2. Illustrative examples Considering the solar system consisting of 16 photovoltaic panels, with TCT connection, under heterogeneous lighting conditions, each photovoltaic panel receives different solar irradiance, as shown in Figure 3-5, irradiance equalization configuration shown in Figure 3-13. 1 2 3 4 11 15 13 14 170 + 200 + 250 + 490 = 1110 W/m2 550 + 140 + 150 + 830 = 1670 W/m2 W/m2 W/m2 W/m2 W/m2 W/m2 W/m2 W/m2 W/m2 5 6 7 8 16 4 12 9 520 + 680 + 480 + 640 = 2320 W/m2 180 + 490 + 290 + 720 = 1680 W/m2 W/m2 W/m2 W/m2 W/m2 W/m2 W/m2 W/m2 W/m2 9 10 11 12 7 5 6 720 + 410 + 550 + 290 = 1970 W/m2 480 + 520 + 680 = 1680 W/m2 W/m2 W/m2 W/m2 W/m2 W/m2 W/m2 W/m2 13 14 15 16 8 3 2 1 10 2 150 + 830 + 140 + 180 = 1300 W/m2 640 + 250 + 200 + 170 + 410 = 1670 W/m W/m2 W/m2 W/m2 W/m2 W/m2 W/m2 W/m2 W/m2 W/m2 Figure 3-5. PV system under non-homogeneous Figure 3-13. Configuration of irradiance equalization PV irradiance energy system corresponding to the G_OP matrix The equalization index is calculated according to the objective function (3-9) (m = 4): 𝐸𝐼 = max (𝐺_𝑂𝑃𝑖 ) − min (𝐺_𝑂𝑃𝑖 ) = 10 𝑖=1,𝑚 𝑖=1,𝑚 3.4.2.3. Comparison and assessment (CT1) Storey et al. 2013 proposed the BWSA algorithm - an algorithm for iterative arrangement, with very fast processing speed, low number of loops but poor results in the majority of cases. An example in Figure 3-14, shows the BWSA algorithm handles with very few iterations and high processing speed. However, the results obtained are not so good as those obtained from DP algorithm proposed above for the same input data. EIBWSA = 110 while EIDP = 10. 𝐸𝐼𝐵𝑊𝑆𝐴 = 1740 − 1630 = 110 Figure3-14. Example of the BWSA algorithm 10
Regarding the processing speed, applied to the system including g photovoltaic panels, m rows and SG as the total solar irradiance, the calculated complexity of algorithm is O(mgSG), taking at least 30.72 ms to deal with Intel Core i5 2.5 Ghz configuration CPU to reconfigure 16 photovoltaic panels with 4 rows. This is the appropriate processing speed for practical solar systems, for example in Palermo (Italy) with a maximum wind speed of 6.4m/s, meaning that for a solar system covering an area of 10-20m2, cloud shading for a few seconds is the worst case for that solar system, requiring a quick switching speed; accordingly, compared to DP's processing speed, the application of DP in practice is more satisfactory. DP algorithm has been analyzed and evaluated in Krishna's published work (SCI-Q1-2019) as one of the few "State of the art" methods that prove the topicality of the proposed algorithm. 3.4.3 Proposal of SmartChoice (SC) algorithm (CT3) SmartChoice is a smart selection algorithm published at (CT2,3) to complement the disadvantages of the DP algorithm. Better results of the two algorithms DP and SC are selected as the “optimal connection configuration”. 1.1.1.1. Algorithm description 3.4.3.1. Application method - Select the photovoltaic panels with the highest solar irradiance, and put them in the row with the lowest total solar irradiance. - In case there are many rows with the same lowest total solar irradiance, put that photovoltaic panel into the row with the lowest index. Figure 3-15. Flowchart of SC algorithm 3.4.3.2. Illustrative examples Considering the solar system consisting of 16 photovoltaic panels, with TCT connection, under heterogeneous lighting conditions, each photovoltaic panel receives different solar irradiance, as shown in Figure 3-16, irradiance equalization configuration shown in Figure 3-22. 11
1 2 3 4 1 6 11 16 620 + 500 + 600 + 300 = 2020 W/m2 620 + 420 + 400 + 240 = 1680 W/m2 W/m2 W/m2 W/m2 W/m2 W/m2 W/m2 W/m2 W/m2 5 6 7 8 3 10 7 15 540 + 420 + 320 + 480 = 1760 W/m2 600 + 460 + 320 + 300 = 1680 W/m2 W/m2 W/m2 W/m2 W/m2 W/m2 W/m2 W/m2 W/m2 9 10 11 12 12 8 13 9 280 + 460 + 400 + 560 = 1700 W/m2 560 + 480 + 360 + 280 = 1680 W/m2 W/m2 W/m2 W/m2 W/m2 W/m2 W/m2 W/m2 W/m2 13 14 15 16 5 2 14 15 360 + 340 + 300 + 240 = 1240 W/m2 540 + 500 + 340 + 300 = 1680 W/m2 W/m2 W/m2 W/m2 W/m2 W/m2 W/m2 W/m2 W/m2 Figure 3-16. PV system under non-homogeneous Hình 3-22. Configuration of irradiance equalization irradiance PV energy system corresponding to the G_OP matrix The equalization index is calculated according to the objective function (3-9) (m = 4): 𝐸𝐼 = max (𝐺_𝑂𝑃𝑖 ) − min (𝐺_𝑂𝑃𝑖 ) = 0 (3-13) 𝑖=1,𝑚 𝑖=1,𝑚 as the optimal arrangement method. 3.4.3.3. Comparison and assessment (CT3) SC algorithm is proposed by the PhD student for the purpose of overcoming special cases of DP algorithm. The DP algorithm gives very good results in most cases; however, in some special cases, it produces results that are not as good as those of SC algorithm, such as the cases in Figure 3-23 and Figure 3-24: EIDP = 1000 while EISC = 850: 150 150 1000 1000 1000 150 150 = 2300 1000 1000 1000 1000 1000 = 2000 1000 1000 1000 1000 1000 1000 = 3000 Matrix G Matrix G_OP by using DP Figure 3-23. Example of irradiance equalization by using DP 150 150 1000 1000 1000 150 150 = 2300 1000 1000 1000 1000 1000 = 2000 1000 1000 1000 1000 1000 1000 = 3000 Matrix G Matrix G_OP by using SC Figure 3-24. Example of irradiance equalization by using SC The SC algorithm has the advantage of a small number of iterations, with O(glogg) complexity. The combination of SC and DP algorithms into a hybrid algorithm with the selection of better results in the two algorithms as the final results will help us find optimal results for the irradiance equalization problem. 12
3.5 Proposal of mathematical model and 02 algorithms for Selecting the optimal switching method The mathematical model, MAA algorithm and improved MAA algorithm are announced in CT8, CT1 and CT3, respectively. 3.5.1 Introduction to the Dynamic Electrical Scheme (DES) switching matrix An example of the operation of DES switching matrix is shown in Figure 3-26. (c) (a) (b) (d) Figure 3-26. Dynamic Electrical Scheme (b-d) corresponds to the connection structure (a-c) Considering the general DES switching matrix for g photovoltaic panels, with a change in connection in m parallel circuits as shown in Figure 3-27. Figure 3-27. Dynamic electrical scheme Figure 3-28. Array Q and matrix S represents the number of opening and closing times of the switching matrix An overview of the number of opening and closing times applied for switching matrix key is shown in Figure 3-28. During the operation of the solar system and the restructuring unit, there is a change in the number of opening and closing of the switching matrix key after each session of restructuring. Convention on the number of opening and closing times - At the initial time: 𝑆𝑖𝑗 = 0 ∀ 𝑖 = 1, . . . , 𝑚; 𝑗 = 1, . . . , 𝑔 (3-14) - During the operation process, when the position of a photovoltaic panel p (p = 1..m) is changed from row i to row ik, the number of opening and closing times of the matrix S will be changed as follows: 𝑆𝑖𝑝 = 𝑆𝑖𝑝 + 1 (3-15) 𝑆𝑖𝑘𝑝 = 𝑆𝑖𝑘𝑝 + 1 Given zP as the number of solar panels subject to change in position in each session of restructuring, the number of opening and closing times of the switching matrix will be 2 x z P. 13
- Given MI the number of opening and closing times in the session of restructuring stepk, we have: 𝑖=𝑚 𝑖=𝑚 𝑗=g 𝑗=g 𝑀𝐼𝑠𝑡𝑒𝑝 𝑘 = ∑(𝑆𝑖𝑗 ) − ∑(𝑆𝑖𝑗 ) (3-16) 𝑠𝑡𝑒𝑝 𝑘 𝑠𝑡𝑒𝑝 𝑘−1 𝑖=1 𝑖=1 𝑗=1 𝑗=1 3.5.2 Proposal of mathematical model (CT8) Figure 3-29. An example of an irradiance equalization configuration with different switching times is given The problem is to select the optimal switching method with the purpose of controlling the switching matrix from the initial configuration G to the G_OP irradiance equalization configuration so as to achieve the minimum number of opening and closing times of S switching matrix key. Figure 3-29 shows an example of the optimal switching method. 3.5.2.1. The problem of finding a configuration with the minimum number of opening and closing times after each session of restructuring. MI is the number of opening and closing times in each session of restructuring, Sij is the number of opening and closing times of a key with row i and column j in the Switching matrix. The objective function sets the minimum number of opening and closing times after each session of restructuring. Objective function: 𝑖=𝑚 𝑖=𝑚 𝑗=g 𝑗=g (𝑀𝐼𝑚𝑖𝑛 )𝑠𝑡𝑒𝑝 𝑘 = ∑(𝑆𝑖𝑗 )𝑠𝑡𝑒𝑝 𝑘 − ∑(𝑆𝑖𝑗 )𝑠𝑡𝑒𝑝 𝑘−1 → 0 (3-18) 𝑖=1 𝑖=1 𝑗=1 𝑗=1 Constraints: 𝑆𝑖𝑗 ≥ 0 𝑖=𝑚 𝑗=g (3-19) ∑(𝑆𝑖𝑗 )𝑠𝑡𝑒𝑝 0 = 0 𝑖=1 𝑗=1 { 14
In which: • m : number of rows in TCT circuit, • g : number of photovoltaic panels; • (𝑀𝐼𝑚𝑖𝑛 )𝑠𝑡𝑒𝑝 𝑘 : the number of opening and closing times in the session of restructuring stepk 3.5.2.2. Balancing the number of opening and closing times of the switching matrix During the restructuring, the photovoltaic panels that are frequently shaded will have the most position changes, resulting in an imbalance in the number of opening and closing times of different keys in the switching matrix. Therefore, the life of the matrix will depend on the life of the lock that closes and opens the most. So in many cases, the switching method with the least number of closing and opening times (calling the least number of closing and opening times as MImin) is not necessarily considered to be optimal, accordingly, it is necessary to choose the other switching method so that the key with the least number of opening and closing times is at the minimum level in order to balance the number of opening and closing of the switching matrix. The objective function on the most number of opening and closing times of the key is constant, still ensuring the minimum number of opening and closing times at each session of switching: max (𝑆𝑖𝑗 ) − max (𝑆𝑖𝑗 ) →0 𝑖=1,𝑚 𝑠𝑡𝑒𝑝 𝑘 𝑖=1,𝑚 𝑠𝑡𝑒𝑝 𝑘−1 𝑗=1,g 𝑗=1,g 𝑖=𝑚 𝑖=𝑚 (3-20) 𝑗=g 𝑗=g 𝑀𝐼𝑠𝑡𝑒𝑝 𝑘 = ∑(𝑆𝑖𝑗 ) − ∑(𝑆𝑖𝑗 ) → (𝑀𝐼𝑚𝑖𝑛 )𝑠𝑡𝑒𝑝 𝑘 𝑠𝑡𝑒𝑝 𝑘 𝑠𝑡𝑒𝑝 𝑘−1 𝑖=1 𝑖=1 { 𝑗=1 𝑗=1 Constraints: Same as the equation (3-19). In which: • m : number of rows in TCT circuit, • g : number of photovoltaic panels; • 𝑀𝐼𝑠𝑡𝑒𝑝 𝑘 : the number of opening and closing times in the session of restructuring stepk • (𝑀𝐼𝑚𝑖𝑛 )𝑠𝑡𝑒𝑝 𝑘 : the minimum number of opening and closing times in the session of restructuring stepk (according to the objective function ( )) 3.5.3 Seeking configuration with the least number of switching times applying MAA (CT1) In a study published in 2015 (CT1), the MAA algorithm was applied in finding the configuration so as to achieve the least number of unlocking times from the initial connection configuration to the optimal connection configuration in each session of restructuring to solve the problem proposed in section 3.5.2.1. Considering the example of dynamic planning algorithm in section 3.4.2.2 on finding the irradiance equalization configuration, we get the results as shown in Figure 3-5 and Figure 3-13. There are 16 panels subject to position movement (maximum movement). 15
3.5.3.1. Application of the MAA algorithm The method of application is performed by the following steps: Step 1: - Consider m rows in the original G matrix as m workers respectively. - Consider m rows in the outcome G_OP matrix as m tasks respectively. - Cost C matrix is built on the principle that: Cij is the number of elements presenting in row i of the G matrix without presenting in row j of the G_OP matrix. Step 2: Apply the MAA algorithm to find the smallest total cost from the C matrix We have: 𝑚 𝑚 (3-22) 𝑧𝑝 = ∑ ∑ 𝐶𝑖𝑗 𝑥𝑖𝑗 = 𝑚𝑖𝑛𝑖𝑚𝑢𝑚 𝑖=1 𝑗=1 with 𝑥𝑖𝑗 = 1 when arranging the worker i with the task j. Step 3: Rearrange the position of rows in the G_OP matrix according to MAA results (the row i in the G matrix corresponds to the row j in the G_OP matrix when xij = 1). Rearrange the order of the elements in each row of the G_OP matrix corresponding to the G matrix. We get zp that represents the least number of solar panel position changes to convert the G initial connection matrix to the G_OP irradiance equalization matrix. So the number of key closing and opening times: 𝑚 𝑚 (3-23) 𝑀𝐼𝑚𝑖𝑛 = 2 × 𝑧𝑃 = 2 × ∑ ∑ 𝐶𝑖𝑗 𝑥𝑖𝑗 = 𝑚𝑖𝑛𝑖𝑚𝑢𝑚 𝑖=1 𝑗=1 satisfy the objective function (3-18) in section 3.5.2.1. 3.5.3.2. Illustrative examples Consider the initial two matrices G and G_OP: 170 200 250 490 550 140 150 830 520 680 480 640 180 490 290 720 720 410 550 290 480 520 680 150 830 140 180 640 250 200 170 410 Matrix G Matrix G_OP 4 3 4 1 4 3 4 1 640 250 200 170 410 4 4 1 3 4 4 1 3 480 520 680 3 2 4 3 3 2 4 3 180 490 290 720 1 3 4 4 1 3 4 4 550 140 150 830 B1. Building cost matrix B2. Apply MAA B3. Rearrange the corresponding rows 3.5.3.3. Results evaluation Based on the position of elements of the matrix G and the matrix G_OP, a connection configuration is obtained in Figure 3-32. 16
1 2 3 4 1 2 3 8 10 = 1670 W/m2 170 + 200 + 250 + 490 = 1110 W/m 2 170 + 200 + 250 + 640 + 410 W/m 2 W/m 2 W/m 2 W/m 2 W/m2 W/m2 W/m2 W/m2 W/m2 5 6 7 8 5 6 7 520 + 680 + 480 + 640 = 2320 W/m2 520 + 680 + 480 = 1680 W/m2 W/m 2 W/m 2 W/m 2 W/m 2 W/m2 W/m2 W/m2 9 10 11 12 9 12 16 4 720 + 410 + 550 + 290 = 1970 W/m2 720 + 290 + 180 + 490 = 1680 W/m2 W/m 2 W/m 2 W/m 2 W/m 2 W/m2 W/m2 W/m2 W/m2 13 14 15 16 13 14 15 11 150 + 830 + 140 + 180 = 1300 W/m2 150 + 830 + 140 + 550 = 1670W/m2 W/m 2 W/m 2 W/m 2 W/m 2 W/m2 W/m2 W/m2 W/m2 (a) Initial configuration (b) Irradiance equalization configuration Figure 3-32. Example of irradiance equalization configuration It can be noticed that the position of 5 photovoltaic panels needs to be changed to change the initial connection configuration to the irradiance equalization configuration: 8, 10, 12, 16, 4, 11. Thus, after applying the MAA algorithm from the initial connection configuration G to the irradiance equalization connection configuration G_OP, the number of photovoltaic panels subject to change in position decreased from 16 to 5. For MAA algorithm with O(m3) complexity and m as the number of rows, in case of using 2.5GHz Intel Core i5 CPU, it only takes 0.122ms for the arrangement of 16 photovoltaic panels in each session of restructuring (CT1), thereby meeting real-time processing requirements. 3.5.4 Balancing the number of opening and closing times of switching matrix with the use of improved MAA (CT3) In the study published in (CT3), the improved MAA algorithm is proposed for the purpose of balancing the number of opening and closing times of the switching matrix, thereby extending the life of the switching matrix compared to the old method (section 3.5.3). 3.5.4.1. Proposal of improved MAA algorithm In case it is desirable to assign the worker u to do the task v, then assign the remaining (nM- 1) tasks to (nM-1) workers, the following method is proposed: Considering the C cost matrix in Figure 3-34. Task Worker 1 2 1 v 1 n 1 C11 1 C11 1 C11 1 2 C21 2 C21 2 C21 2 ... ... ... ... u Cu1 u Cu1 u Cu1 u ... ... ... ... nM 𝐶𝑛𝑀 1 nM 𝐶𝑛𝑀 1 nM 𝐶𝑛𝑀 1 nM Hình 3-34. General C cost matrix 17
Step 1: In the C cost matrix, create a matrix C’ by deleting all Cij values in row u and column v. Step 2: Apply the MAA algorithm (section 2.3.2) to find the minimum total cost with the C’ matrix consisting of the remaining elements (nM-1) x (nM-1). After obtaining result of MAA for the C’ matrix, create the result of the C matrix from the C’ matrix with the addition of Cuv. option. The results on the lowest cost vary as follows: 𝑛𝑀 𝑛𝑀 𝑛𝑀 𝑛𝑀 (3-24) 𝑧𝑃𝑛𝑒𝑤 = ∑ ∑ 𝐶𝑖𝑀𝑗𝑀 𝑥𝑖𝑀𝑗𝑀 + 𝐶𝑢𝑣 → ∑ ∑ 𝐶𝑖𝑀𝑗𝑀 𝑥𝑖𝑀𝑗𝑀 𝑖𝑀 =1 𝑗𝑀 =1 𝑖𝑀=1 𝑗𝑀 =1 𝑖𝑀≠𝑢 𝑗𝑀 ≠𝑣 3.5.4.2. Improved MAA algorithm application method Step 1: - Consider m rows in the original G matrix as m workers respectively. - Consider m rows in the outcome G_OP matrix as m tasks respectively. - Cost C matrix is built on the principle that: Cij is the number of elements presenting in row i of the G matrix without presenting in row j of the G_OP matrix. Step 2: - Suppose we are considering the restructuring session stepk. - Find the maximum value of Sij in the closing and opening matrix Sstepk-1, Sij is the key of solar panel j in the G matrix. - Find the position of row u as the position of photovoltaic panel j in the G matrix. - Find the position of row v as the position of photovoltaic panel j in the G matrix. Apply the improved Munkres algorithm (item 3.5.4.1) to find the minimum total cost from the G matrix while assigning the worker u for the task v. We have: 𝑚 𝑚 𝑚 𝑚 (3-28) 𝑧𝑃𝑛𝑒𝑤 = ∑ ∑ 𝐶𝑖𝑗 𝑥𝑖𝑗 + 𝐶𝑢𝑣 → ∑ ∑ 𝐶𝑖𝑗 𝑥𝑖𝑗 𝑖=1 𝑗=1 𝑖=1 𝑗=1 𝑖≠𝑢 𝑗≠𝑣 With: 𝑥𝑖𝑗 = 1 when arranging the worker i with the task j. In this case 𝑥𝑢𝑣 = 1. Step 3: Rearrange the position of rows in the G_OP matrix according to Munkres results (the row i in the G matrix corresponds to the row j in the G_OP matrix when xij = 1).. Rearrange the order of the elements in each row of the G_OP matrix corresponding to the G matrix. 3.5.4.3. Proof Considering at the generalized restructuring session k-1 The key with the most opening and closing times: 𝑚𝑎𝑥𝑆𝑠𝑡𝑒𝑝𝑘−1 = max (𝑆𝑖𝑗 ) (3-29) 𝑖=1,𝑚 𝑠𝑡𝑒𝑝𝑘−1 𝑗=1,g Considering at the generalized restructuring session k: 18