Tuyển tập Hội nghị Khoa học thường niên năm 2022. ISBN: 978-604-82-7001-8
64
TÍCH HỢP CƠ SỞ TRI THỨC XÁC SUẤT
BẰNG TOÁN TỬ TRUNG VỊ
Nguyễn Văn Thẩm1, Nguyễn Quỳnh Diệp1, Nguyễn Đỗ Kiều Loan2
1Trường Đại học Thủy lợi, email: thamnv@tlu.edu.vn
2Học viện Tài chính
1. GIỚI THIỆU CHUNG
Để xây dựng và duy trì hoạt động của các hệ
thống dựa trên tri thức thì cần xem xét các
phương pháp tích hợp. Tích hợp tri thức
(THTT) có thể được hiểu như là tiến trình tạo
ra một cơ sở tri thức (CSTT) nhất quán từ một
tập các cơ sở tri thức thuộc về các hệ thống
khác nhau. THTT là một bài toán quan trọng
và có rất nhiều các ứng dụng sử dụng tiến trình
THTT. Bài báo này tập trung vào phương pháp
THTT trên môi trường xác suất.
Bài toán THTT trong môi trường xác suất
được định nghĩa như sau: Cho một hồ sơ tri
thức xác suất . Cần xác định một CSTT xác
suất chung * là đại diện tốt nhất cho tập các
CSTT xác suất đã cho.
Gần đây, có hai cách tiếp cận chính để thực
hiện tiến hành tích hợp các CSTT xác suất: (i)
tìm phân phối xác suất chung biểu diễn cho
CSTT xác suất kết quả bằng cách sử dụng các
hàm phân kỳ [2,4]; (ii) sử dụng các toán tử tích
hợp để tính giá trị trung vị của các giá trị xác
suất trong các ràng buộc xác suất đầu vào [1,3].
Trong bài báo này, chúng tôi tập trung vào
phương pháp thứ hai. Bài báo đề xuất một
toán tử tích hợp mới và một thuật toán sử
dụng toán tử này để tiến hành tích hợp các
CSTT dạng xác suất.
2. NỘI DUNG
2.1. Một số khái niệm
Tập hợp tất cả các kết quả của một phép
thử ngẫu nhiên được gọi là không gian mẫu
của phép thử đó, kí hiệu là S. Đặt là một tập
hữu hạn các sự kiện, trong đó mỗi sự kiện là
một tập con của không gian mẫu S.
Định nghĩa 1. [4] Đặt F, G

và

[0,1]
Một ràng buộc xác suất (RBXS) là một biểu
thức có dạng c[
], trong đó c=(F|G).
Nếu F độc lập với G, tức G là lặp thừa, G T,
kí hiệu (F|T). bởi (F). Hai RBXS c1 và c2
được gọi là tương đương về cấu trúc, được kí
hiệu c1
c2, nếu sự kiện bên trái của c1 bằng
sự kiện bên trái của c2 và sự kiện bên phải của
c1 bằng sự kiện bên phải của c2.
Định nghĩa 2. [4] Một cơ sở tri thức (CSTT)
xác suất K là một tập hữu hạn các RBXS:

1n
,k,k
Trong đó: 1
iii
k c[]i ,n

Định nghĩa 3. Một hồ sơ TTXS R trên tập
các sự kiện
là một bộ ,, trong đó
là một tập hữu hạn gồm n sự kiện và là
một đa tập hữu hạn gồm m CSTT xác suất.
Định nghĩa 4. Một hồ sơ TTXS ,
là hồ sơ TTXS nhất quán nếu và chỉ nếu
฀: nhất quán.
2.2. Toán tử tích hợp trung vị
Dựa trên công thức Bordley [1,3], Định
nghĩa sau đây phát biểu về toán tử tích hợp
trung vị theo hệ số của hai giá trị xác suất
trong hai RBXS mà chúng tương đương về
cấu trúc, trong đó mỗi RBXS thuộc một
CSTT xác suất.
Đặt
 
1
11
cc
cc
,


 
Tuyển tập Hội nghị Khoa học thường niên năm 2022. ISBN: 978-604-82-7001-8
65
Định nghĩa 5. [3] Cho
,
,
12
, ,


11 2 2
F|G ; F|G

.
Toán tử tích hợp tích hợp trung vị của hai
giá trị xác suất 1, 2 trong hai RBXS thỏa mãn
các tính chất sau:
(CMT)-Giao hoán (Commutativity).
(
1,
2) = (
2,
1)
(IDP) -Lũy đẳng (Idempotence).
(
1,
2) =
1
(MVP)- Giá trị trung vị (Mean Value
Property). If
1 <
2 thì
1 < (
1,
2) <
2
(SFS)- Tự đối xứng (Self-Symmetry).
(
1, 1
1) = 0.5
(SM)-Đối xứng (Symmetry).
(1
1, 1
2) = 1 (
1,
2)
Định nghĩa 6. Cho ,, 12
, ,


11 2 2
F|G ; F|G

. Khi đó,
RBXS

F
|G [c(
1,
2)] *
. Trong đó,
c(
1,
2) là toán tử tích hợp trung vị theo hệ
số c của hai giá trị xác suất
1,
2 trong hai
RBXS được định nghĩa như sau:
c(
1,
2)

1
12 12
1
12 1 2
21
cc cc
cc c c
 




trong đó,
01c; là một hệ số.
Định lý 1. Toán tử tích hợp c thỏa mãn
tính chất IDP, MVP.
Định nghĩa 7. Cho ,
, 12
, ,
,


11 2 n
F|G , , F|G

 . Khi đó,
RBXS

F
|G [c(
1,…,
n)] *
. Trong đó,
c(
1, …,
n) là toán tử tích hợp trung vị
theo hệ số c của n giá trị xác suất (
1, …,
n)
trong n RBXS được định nghĩa như sau:
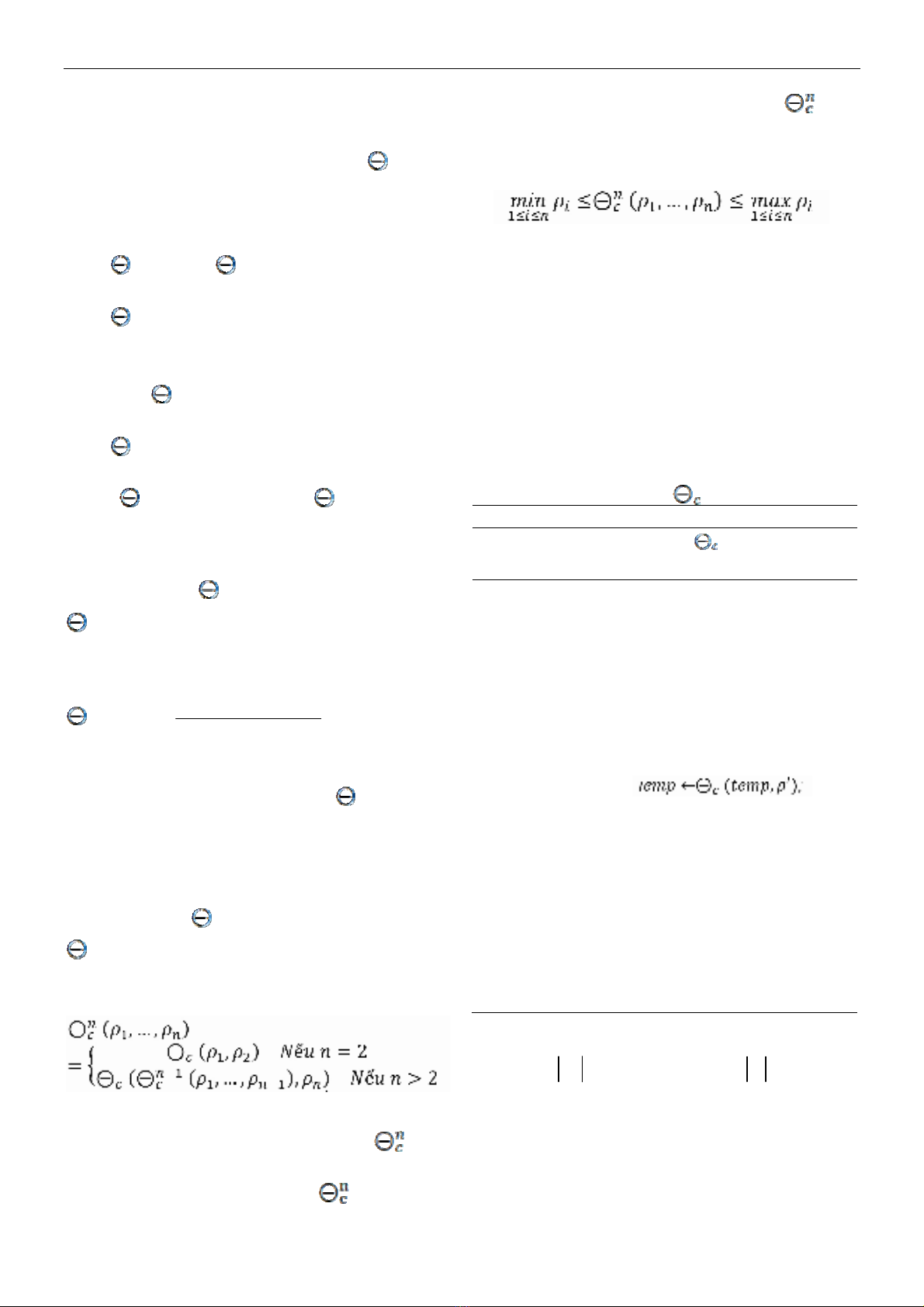
trong đó,
01c; là một hệ số.
Định lý 2. Toán tử tích hợp thỏa
mãn tính chất IDP, MVP.
Như vậy, toán tử tích hợp không thỏa
mãn tính chất CMT, SFS, SM.
Theo Định lý 2, toán tử tích hợp thỏa
mãn tính chất MVP nên dễ dàng có được hệ
quả sau:
Hệ quả 1.
Hệ quả 1 đảm bảo rằng giá trị xác suất của
RBSX mới là giá trị trung bình. Do đó, CSTT
xác suất sau khi tích hợp sẽ phản ánh mức
trung bình của các CSTT xác suất ban đầu.
2.3. Thuật toán đề xuất
Thuật toán đề xuất sau đây được sử dụng
để tích hợp các CSTT xác suất trong một hồ
sơ TTXS nhất quán thành một CSTT xác suất
nhất quán dựa trên toán tử tích hợp trung vị
hợp trung vị theo hệ số .
Thuật toán 1. NewBordley
Input: , và toán tử
Output: *
1: 0;
2: For each i  do
3: For each
i
c
do
4: temp
;
5: For each j  and
j
i do
6: For each
j
c' '
do
7: If c' c then
8:
9:

jj
\c' '
 ;
11: End if;
12: End for
13: End for
14: End for
15:

ii
\c
 ;
16:

**
ctemp ;
17: End for;
Định lý 2. Cho
,
. Đặt

ii
m max : và n. Độ phức
tạp của thuật toán NewBordley là

22
nm.
2.3. Bài toán minh họa
Viện Kỹ thuật tài nguyên nước làm một
cuộc khảo sát về tình trạng ô nhiễm các dòng
Tuyển tập Hội nghị Khoa học thường niên năm 2022. ISBN: 978-604-82-7001-8
66
sông. Các chuyên gia được yêu cầu đưa ra
một số nhận định (tri thức) về: Tỷ lệ mẫu
“nguồn nước bị ô nhiễm” (P), tỷ lệ mẫu
“chứa nước thải sinh hoạt” (D), tỷ lệ mẫu
“chứa nước thải từ khu công nghiệp” (I), tỷ lệ
mẫu nước bị ô nhiễm khi dòng sông chứa
nước thải sinh hoạt, tỷ lệ mẫu nước bị ô
nhiễm khi dòng sông chứa nước thải từ các
khu công nghiệp.
Yêu cầu: Cần tìm một tri thức chung về
các nguyên nhân gây ô nhiễm nguồn nước
của các sông.
Từ kết quả của các chuyên gia cung cấp, ta
thu được hồ sơ CSTT xác suất gồm ba cơ sở
tri thức 123
,, và được thể hiện trong
Bảng 1 cùng với giá trị xác suất mong đợi
(giá trị trung bình-GTTB) của mỗi ràng buộc
sau tiến trình tích hợp. Kết quả tích hợp của
CSTT xác suất 0 khi sử dụng toán tử tích
hợp trung vị với các hệ số khác nhau
cũng được chỉ ra trong Bảng 1.
Bảng 1. Cơ sở tri thức xác suất sau
tiến trình tích hợp

(P) (D) (I) (P|D) (P|I)
1
0.70 0.80 0.60 0.50 0.80
2
0.80 - 0.50 - 0.60
3
0.60 0.70 - 0.70 -
GTTB 0.70 0.75 0.55 0.60 0.70
0.80 0.70 0.50 0.70 0.60
0.66 0.74 0.54 0.58 0.68
0.63 0.76 0.57 0.54 0.72
0.60 0.80 0.60 0.50 0.80
Ta nhận thấy rằng, các kết quả đều thỏa
mãn hệ quả 1.
Hình 1 thể hiện ảnh hưởng của hệ số đến
chất lượng của kết quả tích hợp. Đường màu
đỏ sẫm thể hiện giá trị xác suất của các ràng
buộc mong muốn cần đạt được. Mỗi đường
chấm còn lại thể hiện giá trị xác suất của các
ràng buộc thu được khi hệ số thay đổi. Dựa
trên những đường này có thể thấy rằng các kết
quả thu được gần với kết quả mong muốn.
Hình 1. Mô hình tích hợp CSTT khả năng
3. KẾT LUẬN
Trong bài này, chúng tôi đã đề xuất thêm
một toán tử tích hợp cho các cơ sở tri thức
xác suất. Đồng thời, chúng tôi cũng đề xuất
một thuật toán sử dụng toán tử tích hợp này
để tiến hành tích hợp các cơ sở tri thức dạng
xác suất. Tuy nhiên, bài báo mới tập trung ở
khía cạnh lý thuyết và toán tử tích hợp đề
xuất mới chỉ thỏa mãn hai tính chất đáng
mong đợi. Do đó, trong tương lai chúng tôi sẽ
xây dựng bộ dữ liệu thực tế để kiểm thử các
kết quả đề xuất.
4. TÀI LIỆU THAM KHẢO
[1] Gabriele Kern-Isberner và công sự. 2004.
Belief revision and information fusion on
optimum entropy. International Journal Of
Intelligent Systems. Wiley InterScience.
Volume 19(9):837-857.
[2] Martin Adamcik. 2014. Collective
Reasoning under Uncertainty and
Inconsistency. Luận án tiến sĩ. University of
Manchester, UK.
[3] Van Tham Nguyen và công sự. 2019.
Algorithms for Merging Probabilistic
Knowledge Bases. In Proceedings of the
11th Conference ACIIDS 2019. April 8-11,
2019 and Yogyakarta, Indonesia. Springer.
[4] Van Tham Nguyen và công sự. 2021. A
model for building probabilistic knowledge-
based systems using divergence distances.
Journal of Expert Systems with
Applications. Volume 174: 114494.
Elsevier.