Tiểu luận:TRANSPORT PHENOMENA

Chia sẻ: Nguyen Ha | Ngày: | Loại File: PDF | Số trang:19

Thêm vào BST

Báo xấu

71
lượt xem 5
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Việc sử dụng những mối tương quan trong việc xác định sự truyền động lượng, truyền năng lượng và truyền khối từ pha này sang pha khác dưới những điều kiện trạng thái ổn định đã được trình bày trong chương 4. Mặc dù một vài ví dụ trong chương 4 sử dụng sự bảo toàn vĩ mô, việc giải quyết có hệ thống của những cân bằng này cho sự bảo toàn chemical species, khối lượng và năng lượng không được trình bày. Những bước cơ bản trong sự phát triển của cân bằng trạng thái ổn định vĩ mô được liệt kê như sau

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Tiểu luận:TRANSPORT PHENOMENA

TRƯỜNG ĐẠI HỌC BÁCH KHOA TP.HCM KHOA KỸ THUẬT HÓA HỌC BỘ MÔN CHẾ BIẾN DẦU KHÍ TRANSPORT PHENOMENA (Chương 6&7) GVHD: Mai Thanh Phong HVTH: Phan Hồng Phương Đào Thị Thanh Xuân 2010
6. ĐỊNH LUẬT BẢO TOÀN TRONG TRUYỀN VẬN ỔN ĐỊNH Việc sử dụng những mối tương quan trong việc xác định sự truyền động lượng, truyền năng lượng và truyền khối từ pha này sang pha khác dưới những điều kiện trạng thái ổn định đã được trình bày trong chương 4. Mặc dù một vài ví dụ trong chương 4 sử dụng sự bảo toàn vĩ mô, việc giải quyết có hệ thống của những cân bằng này cho sự bảo toàn chemical species, khối lượng và năng lượng không được trình bày. Những bước cơ bản trong sự phát triển của cân bằng trạng thái ổn định vĩ mô được liệt kê như sau:  Định nghĩa hệ thống của bạn: Một hệ thống là bất cứ vùng nào chiếm thể tích và có một đường ranh giới.  Nếu có thể, hãy vẽ một bức phác họa đơn giản: Một bức phác họa đơn giản giúp chúng ta hiểu được những hình ảnh vật lý.  Liệt kê những giả định: Đơn giản hóa vấn đề phức tạp thành một dạng toán học dễ xử lý bằng cách tiến hành những giả định hợp lý.  Viết phương trình tỷ lệ tóm tắt cho mỗi khái niệm cơ bản liên quan tới vấn đề sắp tới: Khi số hạng tích lũy triệt tiêu trong những trường hợp trạng thái ổn định, những phương trình tỷ lệ vĩ mô dễ xử lý giảm thành những phương trình đại số. Chú ý rằng để có một hệ toán học xác định, số phương trình tỷ lệ độc lập dễ xử lý phải bằng số biến không độc lập.  Sử dụng những tương quan khoa học kỹ sư để đánh giá các hệ số truyền vận: Trong mô hình vĩ mô, những phương trình thực nghiệm thể hiện hiện tượng truyền vận từ pha này sang pha khác đều chứa hệ số truyền vận, như hệ số truyền nhiệt trong định luật làm mát của Newton. Những hệ số này có thể được đánh giá bằng cách sử dụng những tương quan khoa học kỹ sư được đưa ra trong chương 4.  Giải các phương trình đại số. 6.1 SỰ BẢO TOÀN CÁC THÀNH PHẦN HÓA HỌC: Phương trình tỷ lệ tóm tắt được đưa ra bởi phương trình(1.1-1) chứa mỗi lượng bảo toàn. Vì vậy, phát biểu sự bảo toàn cho khối lượng của cấu tử hóa học thứ i dưới điều kiện ổn định được trình bày như sau: ( tỷ lệ khối lượng của i vào) – ( tỷ lệ khối lượng của i ra) + ( tỷ lệ khối lượng phát sinh i) = 0 (6.1-1) Khối lượng của i có thể vào hoặc ra hệ thống bằng 2 phương tiện: (i) Bằng những dòng vào hoặc ra, (ii) Bằng trao đổi khối lượng giữa hệ và môi trường quanh nó qua những ranh giới của hệ thống, ví dụ bề mặt truyền khối. 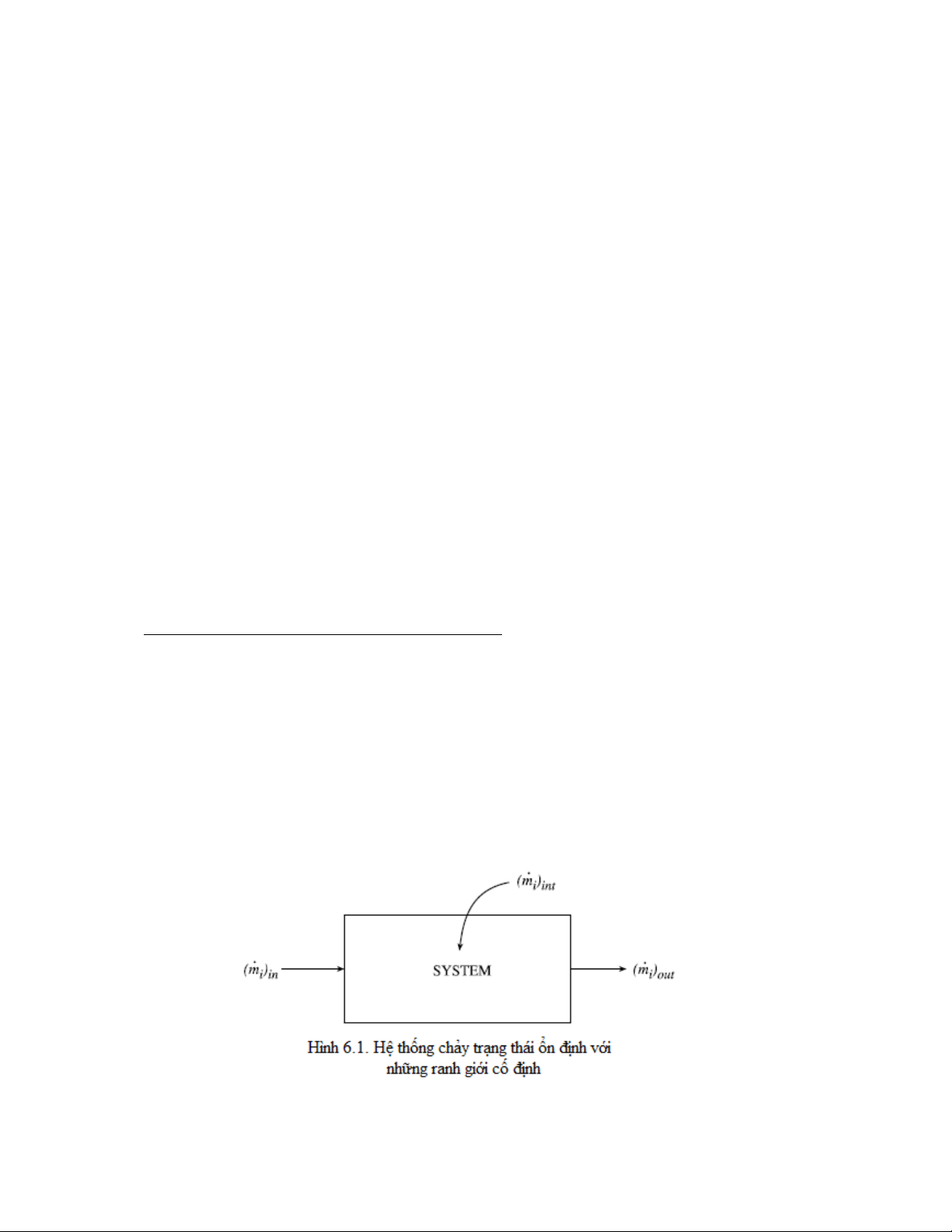Cho một hệ thống với một dòng vào và một dòng ra như hình 6.1, phương trình (6.1-1) có thể được biểu diễn như sau:
Trong đó, tỷ lệ mol của sự sinh ra cấu tử i/ đơn vị thể tích , được thể hiện bởi phương trình (5.3- 27). Số hạng và biểu thị lưu lượng khối vào và ra của cấu tử thứ i, và là khối lượng phân tử của cấu tử thứ i. Tốc độ truyền khối ở bề mặt tiếp xúc, , được biểu diễn như sau: Trong đó là độ chênh lệch nồng độ đặc trưng. Chú ý rằng được xem là dương khi khối lượng được thêm vào hệ. Như đã nói trong phần 2.4.1, lưu lượng khối của cấu tử thứ i, ,được tính bởi: Do đó, phương trình (6.1-2) có dạng: Đôi khi làm việc trên nền tảng mol thì tiện hơn. Chia phương trình (6.1-2) và (6.1-5) cho khối lượng phân tử của cấu tử thứ i, , dẫn đến: và trong đó, và là lưu lượng mol và nồng độ mol của cấu tử thứ i. 6.2 SỰ BẢO TOÀN KHỐI LƯỢNG: Tổng của phương trình (6.1-2) cho tất cả các chất thành phần đưa đến cân bằng tổng khối lượng dưới dạng:
Lưu ý rằng số hạng Bởi vì khối lượng được bảo toàn. Phương trình (6.2-1) chỉ ra rằng tỷ lệ khối lượng tạo thành cho toàn hệ bằng 0. Tuy nhiên, nếu các phản ứng hóa học xảy ra bên trong hệ,một loại riêng có thể được tạo thành. Mặt khác, tổng của phương trình (6.1-6) cho tất cả các chất thành phần đưa đến cân bằng mol tổng như sau: Trong trường hợp số hạng phát sinh khác 0 bởi vì mol thì không được bảo toàn. 6.3. SỰ BẢO TOÀN NĂNG LƯỢNG: Phát biểu sự bảo toàn cho năng lượng tổng dưới điều kiện ổn định có dạng: Định luật thứ nhất của nhiệt động học phát biểu rằng năng lượng tổng có thể không được tạo thành hoặc không bị tiêu hủy. Vì vậy, số hạng lượng năng lượng phát sinh trong phương trình (6.3-1) bằng 0. Năng lượng có thể vào hoặc ra khỏi hệ bằng 2 con đường: (i) bằng dòng vào hoặc ra, (ii) bằng cách trao đổi năng lượng giữa hệ và môi trường xung quanh qua những ranh giới của hệ dưới dạng nhiệt và công. Cho 1 hệ với 1 dòng vào và 1 dòng ra như trong hình 6.2, phương trình (6.3-1) có thể được biểu thị như sau: Trong đó lượng truyền nhiệt giữa các pha, , được biểu diễn:
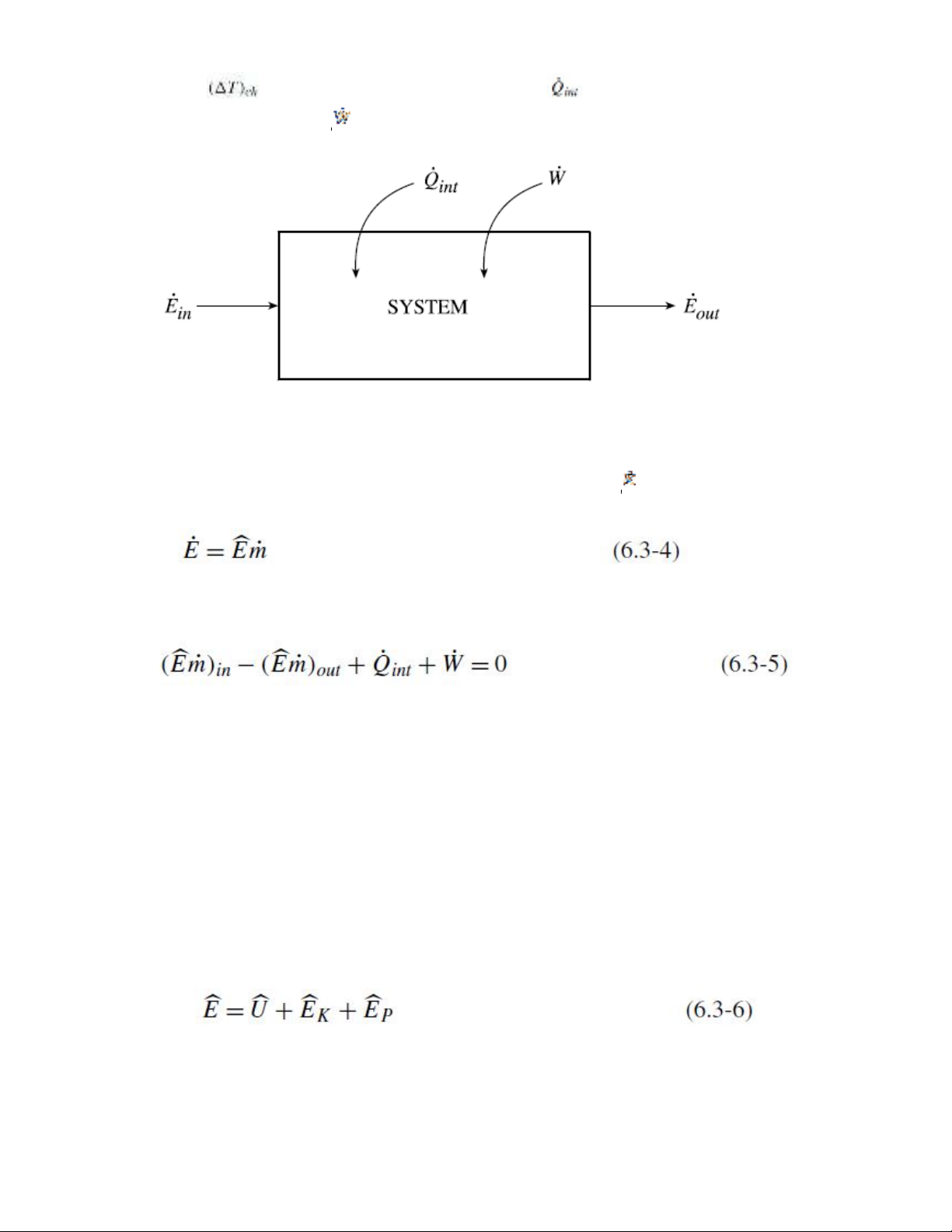
Trong đó là chênh lệch nhiệt độ đặc trưng. Chú ý rằng được coi là dương khi năng lượng được thêm vào hệ. Tương tự, được coi là dương khi công được thực hiện lên hệ. Hình 6.2. Hệ trạng thái ổn định với các ranh giới cố định trao đổi năng lượng dưới dạng nhiệt và công với môi trường. Như đã phát biểu trong phần 2.4.2, lượng năng lượng vào hoặc ra khỏi hệ, , được biểu diễn: Do đó, phương trình (6.3-2) trở thành: Để xác định năng lượng tổng trên đơn vị khối lượng,, xem xét một phi hành gia trên tàu vũ trụ Atlantis. Khi phi hành gia nhìn vào trái đất, anh (chị) ấy thấy rằng trái đất có một động năng ngoài nhờ vào sự quay và chuyển động của nó quanh mặt trời. Trái đất cũng có một động năng trong như một kết quả của tất cả các vật thể, ví dụ, con người, xe cộ, máy bay,..., di chuyển trên bề mặt của nó mà phi hành gia không thể nhìn thấy. Một vật thể luôn được cấu thành bởi những vật thể nhỏ hơn, mỗi vật thể nhỏ có thể có nội năng và ngoại năng. Tổng của nội năng và ngoại năng của những vật thể nhỏ hơn luôn luôn hiển thị như nội năng của những vật lớn hơn. Thảo luận trên chỉ rằng năng lượng tổng của bất cứ hệ nào được biểu diễn là tổng của nội năng và ngoại năng của nó. Động năng và thế năng tạo thành ngoại năng, trong khi năng lượng liên quan đến chuyển động tịnh tiến, quay và dao động của các nguyên tử và phân tử được coi là nội năng. Do đó, năng lượng tổng trên đơn vị khối lượng có thể được biểu diễn: trong đó biểu thị nội năng, động năng và thế năng trên đơn vị khối lượng.Từ phương trình (6.3-6), (6.3-5) ta được:
Tỷ lệ công thực hiện lên hệ bởi môi trường xung quanh được đưa ra bởi: Trong hình 6.2, khi dòng vào hệ, công được thực hiện bởi hệ lên môi trường xung quanh. Chú ý rằng những ranh giới của hệ được cố định trong trường hợp của một hệ ổn định. Do đó, công liên kết với sự thay đổi thể tích thì không bao gồm trong phương trình (6.3-8). Trừ phương trình (6.3-8) cho (6.3-7) và sử dụng định nghĩa của entalpi, ta được: (Phương trình năng lượng trạng thái ổn định) Số hạng động năng và thế năng trong phương trình (6.3-9) được biểu diễn dưới dạng: và Trong đó, g là gia tốc trọng trường và h là độ cao so với mặt phẳng tọa độ. Mặt khác, entalpi phụ thuộc vào nhiệt độ và áp suất. Biến thiên entalpi được biểu diễn: Trong đó β là hệ số giãn nở thể tích và được định nghĩa: Lưu ý rằng:
Khi sự thay đổi động năng và thế năng giữa dòng vào và ra của hệ có thể bỏ qua, phương trình (6.3-9) thu gọn thành: Trong lượng mol, phương trình (6.3-9) và (6.3-15) được viết thành: và 6.3.1 Phương trình năng lượng không có phương trình hóa học: Trong trường hợp không có phản ứng hóa học, phương trình (6.3-9) và (6.3-16) được sử dụng để xác định năng lượng tương tác. Nếu sự thay đổi động năng và thế năng có thể được bỏ qua, khi đó những phương trình này thu gọn thành (6.3-15) và (6.3-17). Việc sử dụng phương trình năng lượng đòi hỏi sự thay đổi entalpi phải được biết hoặc tính toán. Cho một vài chất, như hơi nước và amoniac, giá trị entalpi được liệt kê trong bảng hoặc được đưa ra dưới dạng một đồ thị-hàm của nhiệt độ và áp suất. Trong trường hợp này sự biến đổi entalpi có thể được xác định dễ dàng. Nếu giá trị entalpi không nằm trong bảng, khi đó việc xác định entalpi phụ thuộc vào giá trị của nhiệt độ và áp suất trong quá trình đã cho được đưa ra dưới đây. 6.3.1.1 Áp suất không đổi và không có sự biến đổi pha: Vì dP=0  Tích phân của phương trình (6.3-12) cho : trong đó nhận giá trị 0 tại Tref. Trừ phương trình (6.3-18) cho (6.3-15) cho: Nếu không phụ thuộc nhiệt độ, phương trình (6.3-19) đơn giản thành: 6.3.1.2 Áp suất không đổi với sự thay đổi pha: Khi chúng ta bắt đầu gia nhiệt cho một chất tại áp suất không đổi, biến đổi của nhiệt độ theo thời gian được biểu diễn trong hình 6.3.
Tref= nhiệt độ tại đó diễn ra sự chuyển từ pha γ sang pha σ hoặc ngược lại. Nếu ta chọn entalpy của pha γ bằng 0 tại Tref, khi đó entalpy của pha σ và pha γ tại thời điểm bất kì là: Trong đó tại Tref. 6.3.1.3 Áp suất biến đổi và không có sự thay đổi pha: Entalpy của khí lý tưởng chỉ phụ thuộc nhiệt độ và được biểu diễn bởi phương trình (6.3-18). Do đó, trong những vấn đề liên quan khí lý tưởng, sự biến đổi áp suất không ảnh hưởng đến sự thay đổi entalpy. Trong trường hợp của những chất lưu không nén được, phương trình (6.3-12) đơn giản thành: trong đó, entalpy bằng 0 tại Tref và Pref. Tại áp suất thấp và trung bình, số hạng thứ 2 phía bên phải của phương trình (6.3-22) thường được bỏ qua. 6.3.2 Phương trình năng lượng với một phản ứng hóa học: 6.3.2.1 Nhiệt hóa học: Nhiệt hóa học liên quan những sự thay đổi năng lượng trong những phản ứng hóa học. Hiệu entalpy của 1 mol hợp chất tinh khiết và entalpy tổng của các thành phần cấu tạo nên nó được gọi là nhiệt tạo thành, của hợp chất. Nhiệt tạo thành chuẩn, là nhiệt tạo thành khi cả hợp chất và các thành phần của nó đều ở điều kiện tiêu chuẩn như trong hình 6.4. Kí hiệu ,o, chỉ trạng thái chuẩn. Bởi vì entalpy là một hàm trạng thái,phản ứng có thể diễn ra ở điều kiện tiêu chuẩn hay không là không quan trọng.
Trạng thái chuẩn thường là dạng bền vững của nguyên tố hoặc hợp chất tại nhiệt độ interest, T, và dưới áp suất 1atm (1.013 bar). Do đó, từ „chuẩn” không đề cập tới bất cứ nhiệt độ nào, nhưng lại đề cập tới áp suất 1atm. Các thành phần ở trạng thái chuẩn được quy ước entalpy bằng 0. Nhiệt tạo thành chuẩn của nhiều hợp chất thường được liệt kê trong bảng tại nhiệt độ 25oC và được tìm thấy trong sổ tay kỹ sư hóa học của Perry (1997) và các sách nhiệt động lực học. Ví dụ, nhiệt tạo thành chuẩn của etylbenzen, C8H10, ở trạng thái khí là 29,790J/mol tại 298K. Xem sự tạo thành etylbenzen từ các nguyên tố thành phần của nó qua phản ứng: Nhiệt tạo thành chuẩn : Vì nên ta có: Ta có thể tống quát kết quả này dưới dạng: Nhiệt tạo thành chuẩn của một chất là nhiệt chuẩn của phản ứng trong đó 1 mol của nó được tạo thành từ các đơn chất. Do đó, nhiệt chuẩn của phản ứng, , là hiệu của entalpy tổng của hỗn hợp các sản phẩm tinh khiết và các chất phản ứng ở điều kiện tiêu chuẩn như trong hình 6.5.
Nhiệt chuẩn của phản ứng có thể được tính như sau: Trừ phương trình (6.3-23) cho (6.3-24) dẫn tới: Chú ý rằng nhiệt tạo thành chuẩn của đơn chất bằng 0. Nếu nhiệt được sinh ra trong phản ứng, phản ứng được gọi là tỏa nhiệt. Nếu nhiệt được hấp thụ, phản ứng được gọi là thu nhiệt. Do đó, Nếu nhiệt chuẩn của phản ứng được biết tại 298K, khi đó giá trị của nó tại nhiệt độ khác được tính như sau: Sự biến đổi của nhiệt chuẩn của phản ứng ở áp suất không đổi là hàm của nhiệt độ được đưa ra bởi: Số hạng có thể được biểu diễn như sau: Trừ phương trình (6.3-28) cho phương trình (6.3-27) và lấy tích phân, ta được: 6.3.2.2 Cân bằng năng lượng trong một lò phản ứng khuấy liên tục: Một cân bằng năng lượng trong một lò phản ứng khuấy liên tục với những giả định sau đây là một ví dụ của cân bằng năng lượng với phản ứng hóa học: 1. Những điều kiện trạng thái ổn định chiếm ưu thế. 2. Sự khuấy không đóng góp nhiều năng lượng cho hệ, nghĩa là 3. Thể tích của hệ là hằng số, nghĩa là, lưu lượng thể tích vào và ra bằng nhau.
4. Như một kết quả của sự khuấy trộn lý tưởng, nhiệt độ và nồng độ của hệ là đồng nhất, nghĩa là cout = csys và Tout= Tsys. 5. Những thay đổi của động năng và thế năng được bỏ qua. Vì một phản ứng hóa học liên quan trong trường hợp này, làm việc trên cơ sở mol thì gần đúng hơn. Do đó, phương trình (6.3-17) đơn giản thành: Bất cứ lượng mol nào của hỗn hợp, , có thể được biểu diễn dưới dạng các lượng mol riêng phần, , như: Nhân phương trình (6.3-31) với lưu lượng, , cho: Do đó, phương trình (6.3-30) được biểu diễn: Mặt khác, cân bằng mol vĩ mô cho thành phần i, phương trình (6.1-6), là: Nhân phương trình (6.3-34) với và tổng cho tất cả các thành phần ta được: Trong đó, nhiệt phản ứng được định nghĩa bởi: Trừ phương trình (6.3-35) từ phương trình (6.3-33) mang lại: Chia phương trình (6.3-37) cho lưu lượng thể tích , , được: trong đó là thời gian lưu định nghĩa bởi:
Nhiệt dung mol riêng phần của thành phần i, , liên hệ với entalpy riêng phần bởi: Nếu không phụ thuộc nhiệt độ, khi đó tích phân của phương trình (6.3-40) cho: Trừ phương trình (6.3-40) và (6.3-41) cho (6.3-38) cho: Trong đó: Biểu thức vận tốc phản ứng trong phương trình (6.3-42) chứa hằng số vận tốc phản ứng, k, được thể hiện dưới dạng: Do đó, phương trình (6.3-42) không biến đổi thẳng với nhiệt độ. Khi thành phần nguyên liệu, tỷ lệ và bậc của phản ứng hóa học, nhiệt phản ứng, hằng số vận tốc phản ứng được biết, phát biểu bảo toàn cho các thành phần hóa học và năng lượng chứa 5 biến số, đó là, nhiệt độ vào T in; extent của phản ứng ; nhiệt độ lò phản ứng T; thời gian lưu ; vận tốc truyền nhiệt interphase . Do đó, 3 biến số phải được biết, trong khi đó 2 biến số còn lại có thể được tính từ sự bảo toàn của các thành phần hóa học và năng lượng. Giữa các biến số này, Tin là biến số gắn với nguyên liệu, và T là biến số gắn với sản phẩm, và và là biến số của thiết kế.
7. CÂN BẰNG TRẠNG THÁI KHÔNG ỔN ĐỊNH VĨ MÔ Ở chương này, chúng ta sẽ xem xét các quá trình truyền vận không ổn định giữa các pha chất, giả sử rằng không có sự chênh lệch giữa các pha. Do những biến phụ thuộc, như Nhiệt độ, nồng độ, được coi như đồng nhất trong cùng 1 pha, nên ta có phương trình cân bằng trạng thái vĩ mô là những phương trình vi phân đơn giản theo thời gian. Các bước cơ bản trong sự phát triển của cân bằng không ổn định giống với cân bằng ổn định ở chương 6. Có thể tóm tắt như sau:  Định nghĩa hệ thống của bạn: Một hệ thống là bất cứ vùng nào chiếm thể tích và có một đường ranh giới.  Nếu có thể, hãy vẽ một bức phác họa đơn giản: Một bức phác họa đơn giản giúp chúng ta hiểu được những hình ảnh vật lý.  Liệt kê những giả định  Viết phương trình tỷ lệ tóm tắt cho mỗi khái niệm cơ bản liên quan tới vấn đề quan tâm  Sử dụng những tương quan kỹ thuật để đánh giá các hệ số truyền vận: số lượng các điều kiện ban đầu phải bằng với tổng số bậc của phương trình viết cho hệ đó.  Giải các phương trình vi phân đơn giản. 7.1. CÁC GIÁ ĐỊNH Như đã đề cập ở phương trình(1.1-1), phương trình tổng quát của tốc độ dòng thay đổi của hệ có thể biễu diễn bằng công thức sau: ( tốc độ dòng vào) – ( tốc độ dòng ra) + ( tốc độ phát sinh) = (tốc độ tích lũy) (7.1-1) Lưu ý rằng phân tử và sự phát dòng đối lưu tạo thành khái niệm dòng vào và dòng ra. Xét các biểu thức ở vế trái của phương trình, sự truyền vận phân tử là quá trình chậm nhất. Do đó, trong hệ không ổn định đã cho, biểu thức ở vế phải của phương trình (7.1-1) có thể được coi là không đáng kể nếu (tốc độ truyền vận phân tử) >> ( tốc tộ tích lũy rất nhiều) Hay viết thành: Lưu ý rằng chênh lệch về số lượng/thể tích được biểu diễn dưới dạng:
DifferenceinQuantity / volume Gradient of Quantity/Volume = (7.1- Characteristiclength 4) Mặt khác, thể tích và diện tích đối với độ dài đặc trưng được tính là: Thể tích = (Độ dài đặc trưng)3 (7.1- 5) Diện tích = (Độ dài đặc trưng) 2 (7.1- 6) Thay các phương trình (7.1-4) đến (7.1-6) vào phương trình (7.1-3), ta có ( Diffusity )(Characteristictime)  1 (7.1- (CharacteristicLength) 2 7) Trong các tài liệu ,đại lượng ở vế trái của (7.1-7) gọi là trị số Fourier, ký hiệu là τ Trong các phân tích kỹ thuật, sự lược bỏ những khái niệm trạng thái không ổn định thường được coi gần đúng là trạng thái giả ổn định (pseudo-steady-state). Tuy nhiên, cần phải luôn lưu ý đến điều kiện (7.1-7) ở trên để có thể xem xét sự gần đúng đó. 7.1.2. Không có sự thay đổi của các biến số độc lập trong pha chất đang xem xét Trong các phân tích kỹ thuật, sự thay đổi về nhiệt độ hay nồng độ trong không gian coi như không đáng kể trong lòng chất rắn. Mặc dù sự gần đúng này làm đơn giản hóa việc tính toán, nhưng nó chỉ đúng ở một số trường hợp sau: Hãy xem xét sự truyền vận của một lượng c chất từ pha rắng sang pha lỏng đi qua bề mặt rắn-lỏng. Dưới điều kiện ổn định và không có tái tạo, phương trình thay đổi tốc độ lưu lượng (1.1-1) cho bề mặt có dạng: (Tốc độ truyền φ chất từ pha rắn lên bề mặt) = (tốc độ truyền φ chất từ bề mặt đến pha lỏng) (7.1- 8) Do dòng phân tử của φ chất từ pha rắn vượt trội trong pha lỏng. PT (7.1-8) rút gọn thành: (Dòng phân tử của φ chất từ pha rắn lên bề mặt) = (Dòng φ chất từ bề mặt vào pha lỏng) (7.1- 9) Hay viết thành: [(Transport property)(Gradient of driving force)] solid= [(transfer coeff.)(Difference in Quantity/Volume)] fluid (7.1- 10) Chênh lệch động lực được biểu diễn dưới dạng: Gradient of driving force = (Difference in driving force) / (Characteristic length) (7.1- 11) Ngoài ra,
transport Pr operty (Difference in Quantity/Volume) = ( )( DifferenceInDrivingForce) (7.1- Diffusity 12) Thế (7.1-11) và (7.1-12) vào vế trái và vế phải của phương trình (7.1-10) ta được: Trong đó chỉ số Bi là tỷ lệ: Bi= (Difference in driving force)solid / ((Difference in driving force)fluid Do đó Chỉ số Biot cho truyền nhiệt và khối lượng được xác định bởi: Khi Bi nhỏ, có thể thấy từ (7.1-14) là: (Difference in driving force)solid
Tốc độ truyền khối bề mặt giữa các pha là , được coi là giá trị dương khi khối lượng được công thêm vào cho hệ và được biểu diễn bởi công thức sau: Thế phương trình (7.2-3) vào (7.2-2) ta được Đối với 1 mol chất, phương trình (7.2-2) vào (7.2-4) có dạng: Hoặc 7.3. SỰ BẢO TOÀN TỔNG KHỐI LƯỢNG Tổng của phương trình (7.2-2) đối với tất cả các chất sẽ cho cân bẳng tổng khối lượng của hệ, và có dạng PT trên có được là do khối lượng được bảo toàn nên tổng : =0 Mặt khác, tổng của phương trình (7.2-5) cho tất cả các dòng chất sẽ cho ta phương trình tổng cân bằng mol như sau: Trong đó Dòng tái tạo khác 0, do không bảo toàn về mol. Tổng này chỉ biến mất khi cho tất cả các giá trị j 7.3. SỰ BẢO TOÀN MÔMEN Theo định luật II Niuton về chuyển động, có thể phát biểu sự bảo toàn momen thẳng như sau: Tốc độ thay đổi momen thẳng của vật theo thời gian bằng tổng các lực tác động lên vật.
Ở phần 4.3, chúng ta coi cân bằng lực tác dụng lên một hạt hình cầu, rơi vào chất lỏng với một vận tốc thẳng không đổi vt . Trong trường hợp là hình cầu, có một lực gọi là lực nội lỏng tác động thêm lên hạt đó ngoài các lực bình thường gồm trọng lực, lực nổi, lực kéo. Loại lực này phát sinh khi chất lỏng bao quanh hạt cũng bị tác động từ những phần chất lỏng còn lại, làm thay đổi momen của chất lỏng. Tốc độ thay đổi momen của chất lỏng thể hiện như là một lực bổ sung tác động lên hạt hình cầu, có hướng ngược lại với hướng chuyển động của hạt đó. Do đó phương trình (7.4-1) có thể được viết lại thành Tốc độ thay đổi momen thẳng của hạt cầu= (Trọng lực) - (lực nổi) – (lực kéo) – (Lực nội lỏng) Có thể viết phương trình trên thành: Trong đó DP đường kính hạt cầu rắn; ρP tỷ trọng hạt rắn. ρ: là tỷ trọng chất lỏng. Rút gọn (7.4-3) thành: D P f :Friction Factor thường được cho dưới dạng là hàm của hằng số Reynold (ReP)=  Thay vào ta có: D 2 P d . Re P 3 (ρP + 0,5 ρ) = Ar – f Re 2 P (7.4-  dt 4 6) Trong đó Ar: Chỉ số acsimet, được xác định bằng công thức (4.3-6). Lưu ý khi hạt đạt đến vận tốc thẳng thì d ReP/dt = 0, Phương trình (7.4-6) giản lược thành (4.3-4). Lấy tích phần phương trình (7.4- 6) ta được: (7.4-8) Phương trình trên có thể được đánh giá bằng số học 7.5. SỰ BẢO TOÀN NĂNG LƯỢNG Có thể phát biểu cho tổng năng lượng dưới các điều kiện không ổn định như sau:
Đối với hệ (như hình 7.2), theo diễn giải ở phần 6.3, phương trình trên viết lại thành: Lưu ý, ngược với hệ có dòng ổn định, biên giới của hệ ở đây không cố định một chỗ. Do đó, bên cạnh lực shaft và flow work, thì lực phát sinh do sự co/giãn ranh giới của hệ phải được tính đến. Do đó ta có: Trong đó A: lực phát sinh do sự co/giãn ranh giới của hệ; B: shaft work; C: Flow work Thế (7.5-3) vào (7.5-2) và sử dụng định nghĩa enthalpy: H= U + PV, ta có: Đây là phương trình năng lượng tổng quát. Lưu ý là ở điều kiện ổn định, phương trình (7.5-4) trở thành phương trình (6.3-9). Đối với hệ mol chất, có thể viết công thức dưới dạng sau: Khi những sự thay đổi động năng và thế năng giữa dòng vào và ra của hệ cũng như trong bản thân hệ được coi như không đáng kể thì PT (7.5-4) có thể viết thành: Vế phải ở trên viết lại thành:
Thế (7.5-7) vào (7.5-6) cho ta PT sau: Với mỗi mol chất, ta có: