ng dng tích phân tính din tích, th tích
217
NG DNG TÍCH PHÂN TÍNH DIN TÍCH, TH TÍCH

=
==
=
f

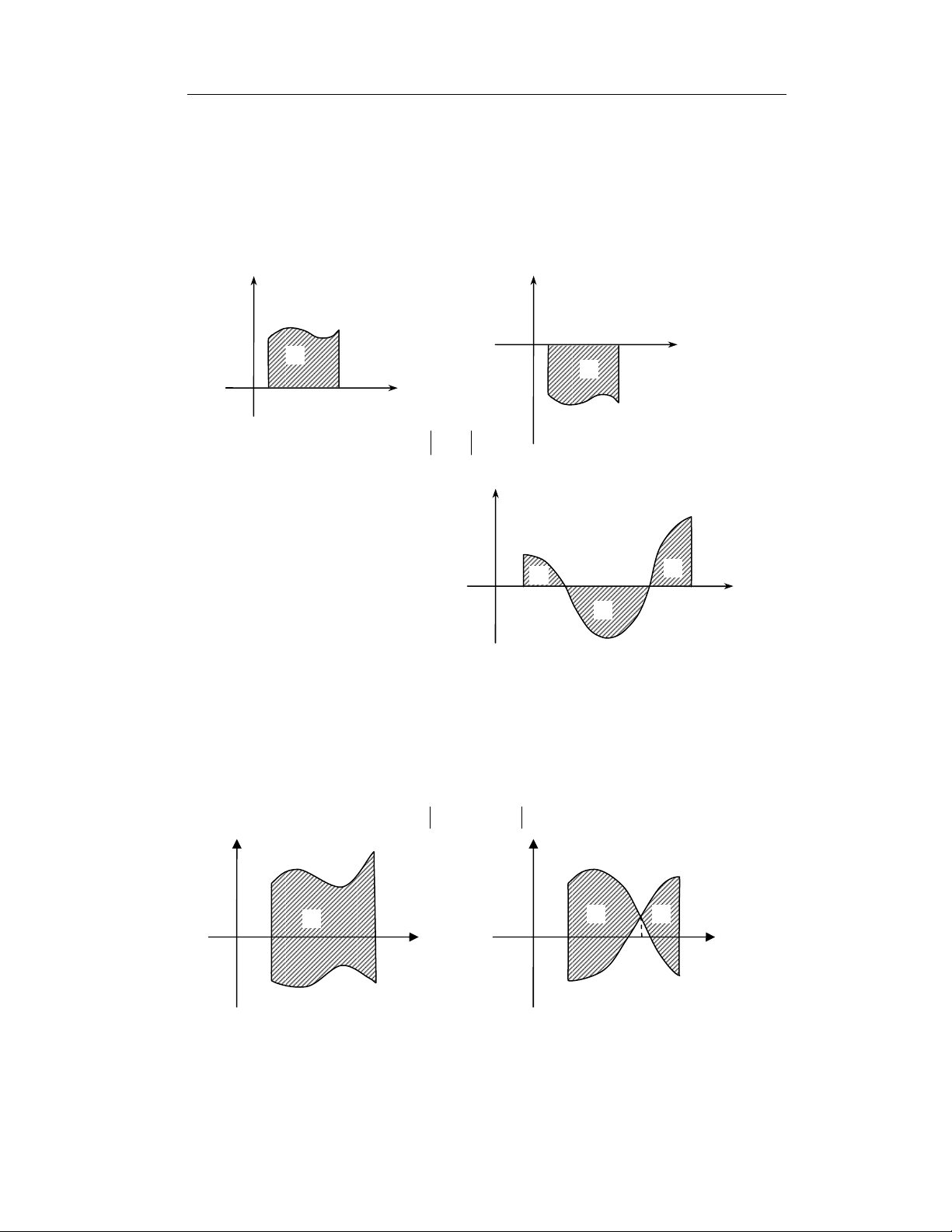
1. DIN TÍCH HÌNH PHNG GII HN BI 1 NG CONG:
Tìm din tích hình phng S gii hn bi
(
)
(
)
:
: 0
,
=
=
= =
y f x
Ox y
x a x b

:
( )
=
b
a
S f x dx
a
a
.
( )
=
b
a
S f x dx
a nu
f
(
x
)
≥
0
b
.
( )
= −
b
a
S f x dx
nu
f
(
x
)
≤
0
c
.
( ) ( ) ( )
= − +
c d b
a c d
2. DIN TÍCH HÌNH PHNG GII HN BI 2 NG CONG:
Tìm din tích hình phng S gii hn bi
(
)
( )
( )
( )
1
2
:
:
,
=
=
= =
y f x
y g x
x a x b

( ) ( )
= −
b
a
S f x g x dx
O a b
x
f
(
x
) < 0
y
S
f
(
x
) < 0
f
(
x
) > 0
f
(
x
) > 0
y
O a b
x
c d
S
2
S
3
S
1
x
y
a b O
S
f
(
x
)
g(
x
)
x
y
a b O
f
(
x
)
g(
x
)
c
g(
x
)
f
(
x
)
S
2
S
1
f
(
x
) > 0
O a b
x
y
S
Chng II. Nguyên hàm và tích phân
−
−−
−
Trn Phng
218
a
a.
( ) ( )
( )
= −
b
a
S f x g x dx
nu
f
(
x
)
≥
g(
x
)
∀
x
∈
[a, b]
b.
( ) ( )
( )
= −
b
a
S g x f x dx
nu
f
(
x
)
≤
g(
x
)
∀
x
∈
[a, b]
c.
( ) ( )
( )
( ) ( )
( )
= − + −
c b
a c
S f x g x dx g x f x dx
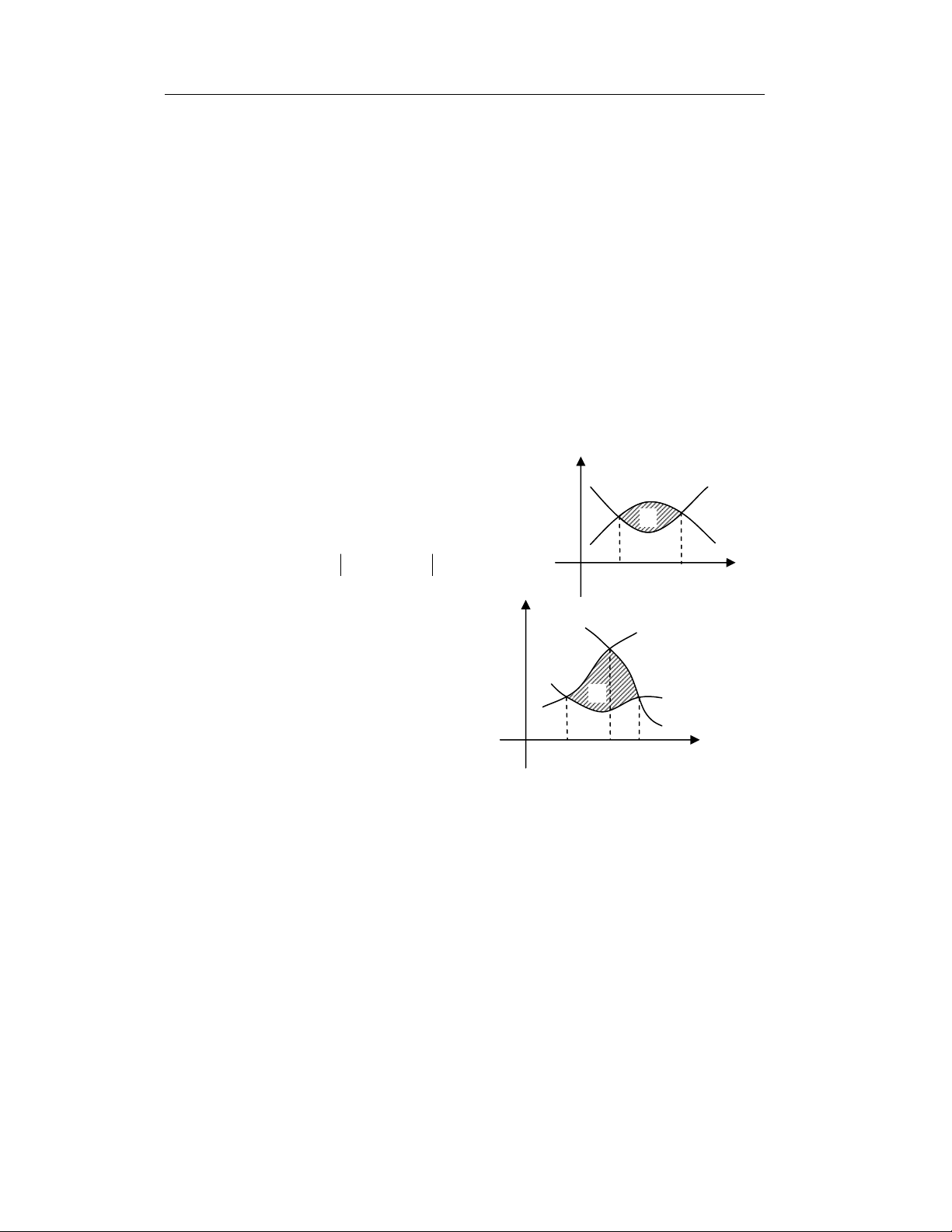
3. DIN TÍCH HÌNH PHNG GII HN BI CÁC NG CONG T CT KHÉP KÍN

Tìm din tích hình phng S gii hn bi
(
)
(
)
( )
( )
1
2
=
=
: y f x
: y g x
Bc 1:
Gii phơng trình:
( ) ( )
=
= ⇔
=
x a
f x g x
x b
Bc 2:
S dng
( ) ( )
= −
b
a
S f x g x dx

Tìm din tích hình phng
S gii hn bi
(
)
( )
( )
( )
( )
( )
1
2
3
=
=
=
: y f x
: y g x
: y h x
Bc 1:
Gii phơng trình tơng giao
→
tìm hoành giao im
(
)
(
)
( )
( )
( )
( )
1 2
2 3
3 1
C
A
B
≡ ∩
≡ ∩
≡ ∩
Bc 2:
S dng
( ) ( )
( )
( ) ( )
( )
= − + −
c b
a c
S f x h x dx g x h x dx
4. CHÚ Ý:
Cn phi in "vdt" vào kt qu cui cùng trong các bài toán
tính din tích hình phng
(
)
(
)
( )
( )
( )
( )
1 2
2 3
3 1
C
A
B
≡ ∩
≡ ∩
≡ ∩
gii phơng trình
f
(
x
)
=
g
(
x
)
gii phơng trình
g
(
x
)
=
h
(
x
)
gii phơng trình
h
(
x
)
=
f
(
x
)
x
y
a b O
f
(
x
)
g(
x
)
S
S
g(
x
)
f
(
x
)
h(
x
)
a b c
x
y
O
A
B
C
ng dng tích phân tính din tích, th tích
219
5. CÁC BÀI TP MU MINH HA
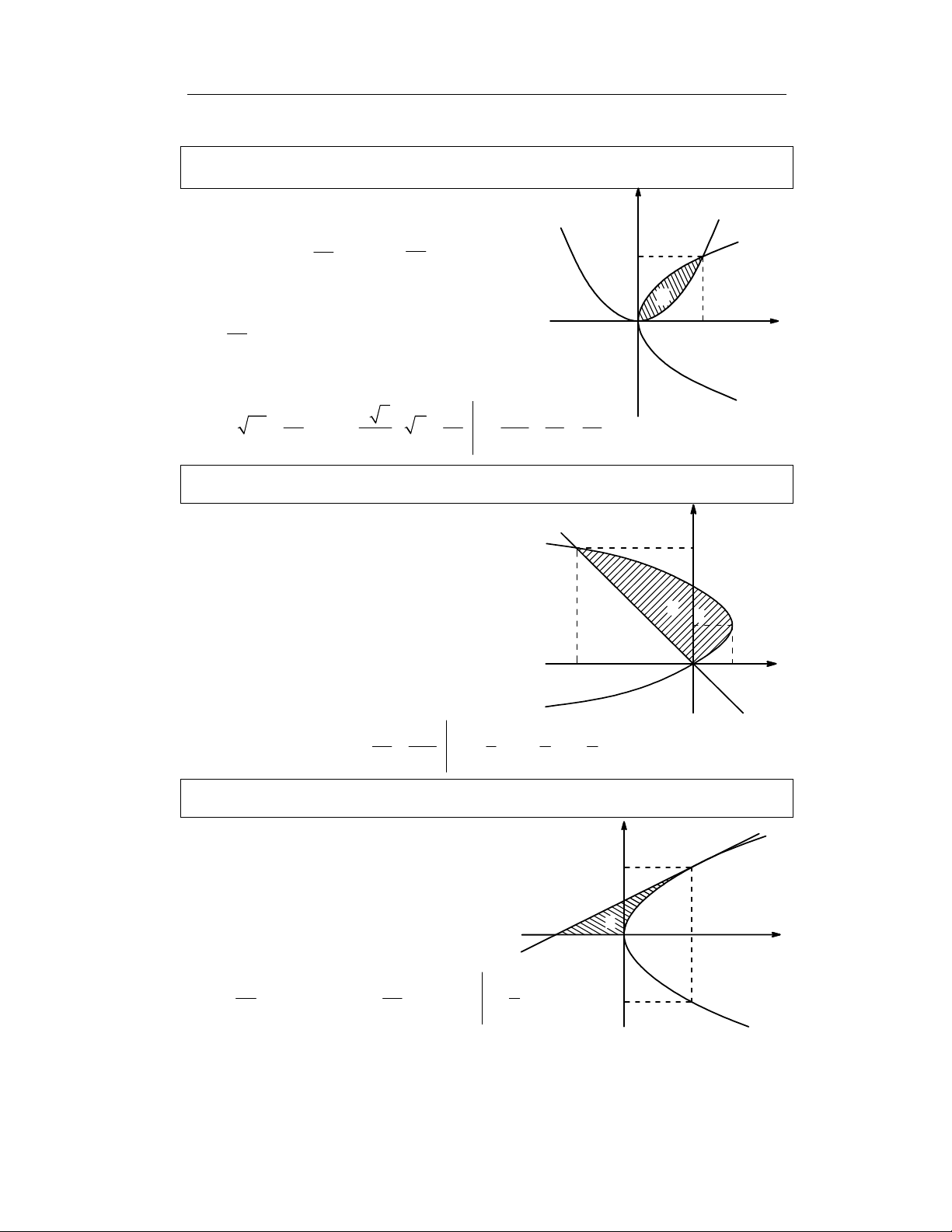
Bài 1.
Tính S:
( ) ( )
{
}
( )
2 2
1 2
P : x ay ; P : y ax a 0
= = >
Gii
( ) ( )
4
2
2
2
1 2
22
4
4 3
2
2
2
x
xy
y
P P : aa
y ax y ax
xax
x a x x 0, y 0
a
x a, y a
y ax
y ax
=
=
∩ ⇔
==
=
= = =
⇔ ⇔ ⇔
= =
=
=
a
a
2 3 2 3 2
00
x 2 a x 2a a a
S ax dx x x
a 3 3a 3 3a 3
= − = − = − =
(vdt)
Bài 2.
Tính S:
( )
( )
{
}
2
: y 2y x 0 ; D : x y 0
− + = + =
Gii
( )
( )
2
: y 2y x 0
D : x y 0
− + =
+ =
⇔
( )
( )
2
: x y 2y
D : x y 0
= − +
+ =
( )
( )
2
y 0; x 0
D : y 2y y 0
y 3; x 3
= =
∩ − + + = ⇔
= = −
( )
( )
( )
3 3
2 2
0 0
S y 2y y dy y 2y y dy
= − + − − = − + +
( )
3
33 2
2
00
y 3y 1 3 9
y 3y dy 27 9
3 2 3 2 2
= − + = − + = − ⋅ + ⋅ =
(vdt)
Bài 3.
Tính S:
(
)
(
)
{
}
2
P : y 2x ; D : x 2y 2 0 ; Ox : y 0
= − + = =
Gii
( ) ( )
( )
2
2
2
y 2 2y 2
y 2x
P D x 2y 2 x 2y 2
y 2
y 4y 4 0
x 2
x 2y 2
= −
=
∩ ⇔ ⇔
= − = −
=
− + =
⇔ ⇔
=
= −
( )
2
22 3
2
00
y y
8
S 2y 2 dy y 2y
2 6 6
= − − = − + =
(vdt)







Chng II. Nguyên hàm và tích phân
−
−−
−
Trn Phng
220
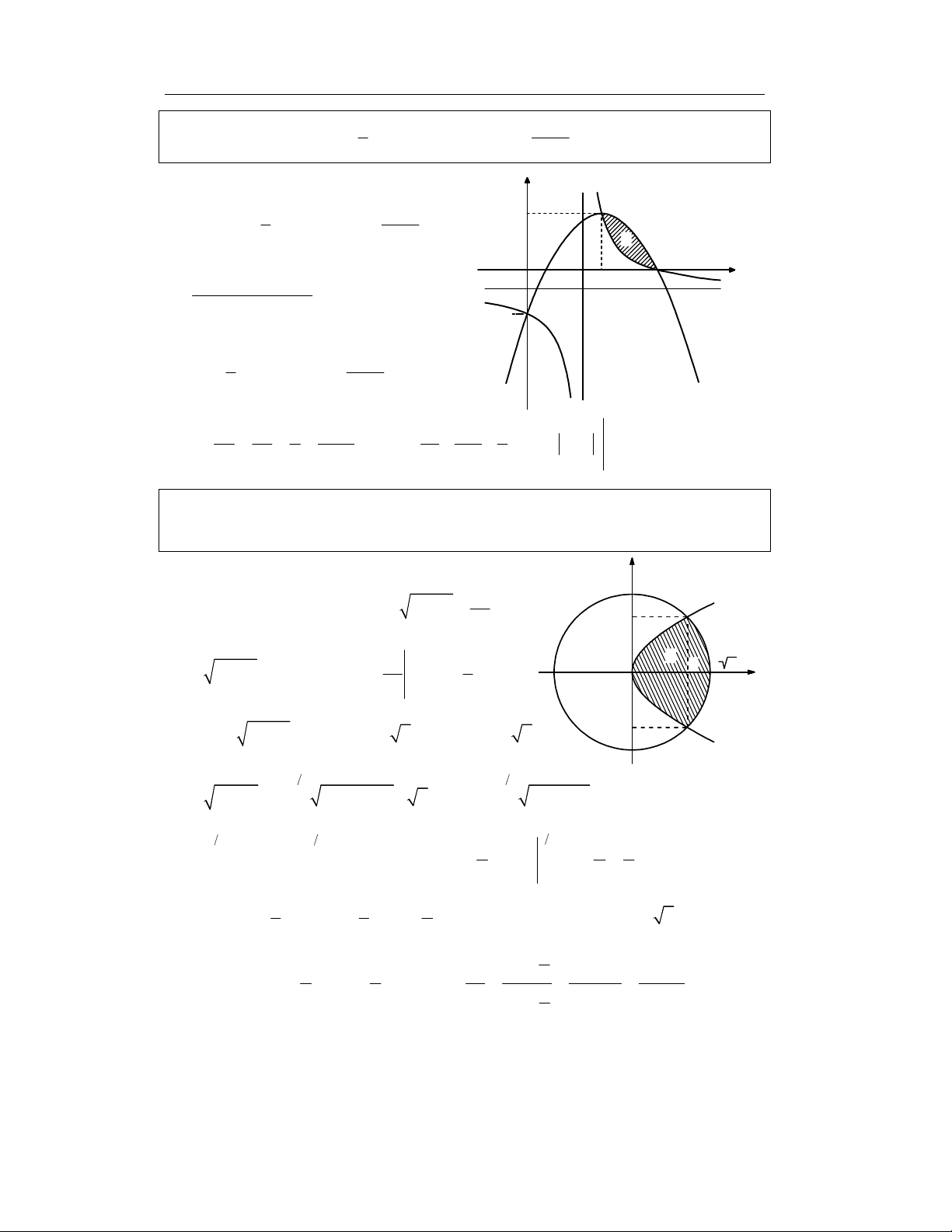
Bài 4.
Tính S:
( )
( )
( )
{
}
2
1 7 x
P : y x 8x 7 ; H : y
3 x 3
−
= − − + =
−
Gii
( ) ( )
( )
( )
( )
2
2
1 7 x
P H : x 8x 7
3 x 3
x 0
x x 11x 28
0 x 4
3 3 x
x 7
−
∩ − − + =
−
=
− +
⇔ = ⇔ =
−=
( )
7
2
4
1 7 x
S x 8x 7 dx
3 x 3
−
= − − + −
−
72
4
x 8x 4 4
dx
3 3 3 x 3
= − + − −
−
7
3 2
4
x 4x 4
x 4ln x 3 9 8ln 2
9 3 3
= − + − − − = +
(vdt)
Bài 5.
Cho:
( )
( )
{
}
2 2 2
P : y 2x ; C : x y 8
= + =
.
(P) chia (C) thành 2 phn, tìm t s din tích ca 2 phn ó.
Gii
Nhìn vào th ta có:
22
2
2
0
y
S 2 8 y dy
2
= − −
2
2 2 3
2 2
0 0 0
y 8
2 8 y dy y dy 2I 2I
3 3
= − − = − = −
Xét
2
2
0
I 8 y dy
= −
. t
y 2 2 sin t dy 2 2 cos tdt
==
( )
4 4
2
2 2 2
0 0 0
4
4 4
2
0
0 0
I 8 y dy 8 8sin t.2 2 cos tdt 8 1 sin t cos tdt
1 1
8 cos t dt 4 1 cos 2t dt 4 t sin 2t 4 2
2 4 2
π π
π
π π
= − = − = −
π
= = + = + = + = π +
Vy
2
8 8 4
S 2I 2 4 2
3 3 3
= − = π + − = π +
(vdt). Ta có:
( )
2
1 2
S S 2 2 8
+ = π = π
(
)
1
4
4
S 8 2 6
3
3
= π − π + = π −
(vdt)
1
2
4
6
S
18 4 9 2
3
4
S 6 4 3 2
2
3
π −
π − π −
= = =
π + π +
π +




ng dng tích phân tính din tích, th tích
221
Bài 6.
Tính S:
( ) ( )
{
}
2
P : y x 4x 3 ; D : y x 3
= − + = +
Gii
( ) ( )
2 2
2 2
x 3 x 4x 3 x 5x 0 x 0, y 3
P D :
x 5, y 8
x 3 x 4x 3 x 3x 6
+ = − + − = = =
∩ ⇔ ⇔
= =
+ = − + − − +
( )
2
x 1
P Ox : y 0 x 4x 3 0
x 3
=
∩ = − + = ⇔
=
( )
( )
( )
( )
( )
( )
1
2
0
3
2
1
5
2
3
S x 3 x 4x 3 dx
x 3 x 4x 3 dx
x 3 x 4x 3 dx
= + − − + +
+ + + − + +
+ + − − +
( ) ( ) ( )
1 3 5
2 2 2
0 1 3
x 5x dx x 3x 6 dx x 5x dx
= − + + − + + − +
1 3 5
3 2 3 2 3 2
0 1 3
x 5x x 3x x 5x 109
6x
3 2 3 2 3 2 6
= − + + − + + − + =
(vdt)
Bài 7.
Tính S:
( ) ( )
( )
2
1 2
3x 12x
C : y 1 2sin ; C : y 1 ; D : x
2 2
π
= − = + =
π
Gii
( )
2
1
3x
C : y 1 2 sin cos3x
2
= − =
Nhìn vào th ta có:
ANOI OIK
S S S
3
= −
66
0
0
7 1
3 cos3xdx 2 sin3x 2 1
2 2
ππ
+ π
= ⋅ − = π − = π −
Bài 8.
Tìm din tích hình phng S gii hn bi
(P): y
=
x
2
−
2x
+
2 và các tip tuyn ca (P)
i qua A(2;
−
2).


ππ
π