
1
B`
AI T ˆ
A
.P PHU
.O
.NG TR`
INH VI PH ˆ
AN
1)
●✐❛
✬✐ ♣❤✉✳♦✳♥❣ tr✏✒♥❤✿
2xy′y” = y′2−1
HD gia
’i:
❉
✲✕❛
✳t
y′=p: 2xpp′=p2−1
❱✓♦✳✐
x(p2−1) 6= 0
t❛ ❝♦✓✿
2pdp
p2−1=dx
x⇔p2−1 = C1⇔p=±√C1x+ 1
p=dy
dx =√C1+ 1 ⇒y=2
3C1
(C1x+ 1)3
2+C2
2)
●✐❛
✬✐ ♣❤✉✳♦✳♥❣ tr✏✒♥❤✿
√y.y” = y′
HD gia
’i:
❉
✲✕❛
✳t
y′=p⇒y” = pdp
dy
✭❤❛✒♠ t❤❡♦ ②✮✳ P❤✉✳♦✳♥❣ tr✏✒♥❤ tr♦✳
✬t❤❛✒♥❤✿
√ypdp
dy =p
❱✓♦✳✐
p6= 0
t❛ ❞✖✉✳♦✳
✳❝ ♣❤✉✳♦✳♥❣ tr✏✒♥❤✿
dp =dy
√y⇒p= 2√y+C1⇔dy
dx = 2√y+C1⇒
dx =dy
2√y+C1
❚✒✉✳❞✖♦✓ ♥❣❤✐❫❡
✳♠ t❫♦
✬♥❣ q✉❛✓t✿
x=√y−C1
2ln |2√y+C1|+C2
◆❣♦❛✒✐ r❛
y=c
✿ ❤✕❛
✒♥❣ ❝✉
⑦♥❣ ❧❛✒ ♥❣❤✐❫❡
✳♠✳
3)
●✐❛
✬✐ ♣❤✉✳♦✳♥❣ tr✏✒♥❤✿
a(xy′+ 2y) = xyy′
HD gia
’i: a(xy′+ 2y) = xyy′⇒x(a−y)y′=−2ay
◆❫❡
✓✉
y6= 0
✱ t❛ ❝♦✓ ♣❤✉✳♦✳♥❣ tr✏✒♥❤ t✉✳♦✳♥❣ ❞✖✉✳♦✳♥❣ ✈✓♦✳✐
a−y
ydy =−2a
xdx ⇔x2ayae−y=C
◆❣♦❛✒✐ r❛
y= 0
❝✉
⑦♥❣ ❧❛✒ ♥❣❤✐❫❡
✳♠✳
4)
●✐❛
✬✐ ♣❤✉✳♦✳♥❣ tr✏✒♥❤✿
y” = y′ey
HD gia
’i:
❉
✲✕❛
✳t
y′=p⇒y” = pdp
dy
t❤❛② ✈❛✒♦ ♣❤✉✳♦✳♥❣ tr✏✒♥❤✿
pdp
dy =pey
❱✓♦✳✐
p6= 0 : dp
dy =ey⇔p=ey+C1⇒dy
dx =ey+C1⇔dy
ey+C1
=dx
❱✓♦✳✐
C16= 0
t❛ ❝♦✓✿
Rdy
ey+C1
=1
C1Rey+C1−ey
ey+ 1 dy =1
C1
(y−Reydy
ey+C1
) = y
C1−
1
C1
ln(ey+C1)
♥❤✉✳✈❫❛
✳②✿
Rdx
ey+C1
=
−e−ynˆe
´uC1= 0
1
C1
(y−ln |ey+C1|) nˆe
´uC16= 0.
◆❣♦❛✒✐ r❛
y=C:
❤✕❛
✒♥❣ ❧❛✒ ♠❫♦
✳t ♥❣❤✐❫❡
✳♠
5)
●✐❛
✬✐ ♣❤✉✳♦✳♥❣ tr✏✒♥❤✿
xy′=y(1 + ln y−ln x)
✈✓♦✳✐
y(1) = e
w w w .VNM ATH.com

2
HD gia
’i:
❉
✲✉✳❛ ♣❤✉✳♦✳♥❣ tr✏✒♥❤ ✈❫❡
✒✿
y′=y
x(1 + ln y
x)
✱ ❞✖✕❛
✳t
y=zx
❞✖✉✳♦✳
✳❝✿
xz′=zln z
•zln z6= 0 ⇒dz
zln z=dx
x⇒ln z=Cx
❤❛②
ln y
x=Cx ⇔y=xeCx
y(1) = e→C= 1.
❱❫❛
✳②
y=xex
6)
●✐❛
✬✐ ♣❤✉✳♦✳♥❣ tr✏✒♥❤✿
y”(1 + y) = y′2+y′
HD gia
’i:
❉
✲✕❛
✳t
y′=z(y)⇒z′=zdz
dy
t❤❛② ✈❛✒♦ ♣❤✉✳♦✳♥❣ tr✏✒♥❤✿
dz
z+ 1 =dy
y+ 1
⇒z+ 1 = C1(y+ 1) ⇒z=C1y+C1−1⇔dy
C1y+C1−1=dx (∗)
•C1= 0 ⇒(∗)
❝❤♦
y=C−x
•C16= 0 ⇒(∗)
❝❤♦
1
C1
ln |C1y+C1−1|=x+C2
◆❣♦❛✒✐ r❛
y=C
❧❛✒ ♥❣❤✐❫❡
✳♠✳
❚♦✓♠ ❧❛
✳✐ ♥❣❤✐❫❡
✳♠ t❫♦
✬♥❣ q✉❛✓t✿
y=C, y =C−x;1
C1
ln |C1y+C1−1|=x+C2
7)
●✐❛
✬✐ ♣❤✉✳♦✳♥❣ tr✏✒♥❤✿
y′=y2−2
x2
HD gia
’i:
❇✐❫❡
✓♥ ❞✖❫♦
✬✐ ✭✸✮ ✈❫❡
✒❞❛
✳♥❣✿
x2y′= (xy)2−2 (∗)
❉
✲✕❛
✳t
z=xy ⇒z′=y+xy′
t❤❛② ✈❛✒♦
(∗)
s✉② r❛✿
xz′=z2+z−2⇔dz
z2+z−2=dx
x⇔3
rz−1
z+x=Cx
❱❫❛
✳② ❚P❚◗✿
xy −1
xy + 2 =Cx3.
8)
●✐❛
✬✐ ♣❤✉✳♦✳♥❣ tr✏✒♥❤✿
yy” + y′2= 1
HD gia
’i:
❉
✲✕❛
✳t
y′=z(y)⇒y” = z.dz
dy
❇✐❫❡
✓♥ ❞✖❫♦
✬✐ ♣❤✉✳♦✳♥❣ tr✏✒♥❤ ✈❫❡
✒✿
z
1−z2dz =dy
y⇔z2= 1 + C1
y2
⇒dy
dx =±r1 + C1
y2⇔ ±Rdy
r1 + C1
y2
=dx ⇒y2+C1= (x+C2)2
◆❣❤✐❫❡
✳♠ t❫♦
✬♥❣ q✉❛✓t✿
y2+C1= (x+C2)2
9)
●✐❛
✬✐ ♣❤✉✳♦✳♥❣ tr✏✒♥❤✿
2x(1 + x)y′−(3x+ 4)y+ 2x√1 + x= 0
HD gia
’i: y′−3x+ 4
2x(x+ 1).y =−1
√x+ 1;x6= 0, x 6=−1
◆❣❤✐❫❡
✳♠ t❫♦
✬♥❣ q✉❛✓t ❝✉
✬❛ ♣❤✉✳♦✳♥❣ tr✏✒♥❤ t❤✉❫❛
✒♥ ♥❤❫❛
✓t✿
Rdy
y=R3x+ 4
2x(x+ 1)dx =R(2
x−1
2(x+ 1))dx ⇔y=Cx2
√x+ 1
w w w .VNM ATH.com

3
❇✐❫❡
✓♥ t❤✐❫❡♥ ❤✕❛
✒♥❣ s❫♦
✓✿
C′=−1
x2⇒C=−1
x+ε.
❱❫❛
✳② ♥❣❤✐❫❡
✳♠ t❫♦
✬♥❣ q✉❛✓t✿
y=x2
√x+ 1(1
x+ε)
10)
●✐❛
✬✐ ♣❤✉✳♦✳♥❣ tr✏✒♥❤✿
y” = e2y
t❤♦❛
✬
(y(0) = 0
y′(0) = 0
HD gia
’i:
❉
✲✕❛
✳t
z=y′→y” = z.dz
dy
♣❤✉✳♦✳♥❣ tr✏✒♥❤ tr♦✳
✬t❤❛✒♥❤
z.dz
dy =e2y⇔z2
2=e2y
2+ε
y′(0) = y(0) = 0 ⇒ε=−1
2.
❱❫❛
✳②
z2=e2y−1.
❚✒✉✳❞✖♦✓✿
z=dy
dx =√e2y−1⇒Zdy
√e2y−1=x+ε. d¯ˆo
’i biˆe
´nt=√e2y−1
arctg√e2y−1 = x+ε
y(0) = 0 ⇒ε= 0.
❱❫❛
✳② ♥❣❤✐❫❡
✳♠ r✐❫❡♥❣ t❤♦❛
✬❞✖✐❫❡
✒✉ ❦✐❫❡
✳♥ ❞✖❫❡
✒❜❛✒✐✿
y=1
2ln(tg2x+ 1).
11)
❚✏✒♠ ♥❣❤✐❫❡
✳♠ r✐❫❡♥❣ ❝✉
✬❛ ♣❤✉✳♦✳♥❣ tr✏✒♥❤✿
xy′+ 2y=xyy′
t❤♦❛
✬♠❛
⑦♥ ❞✖✐❫❡
✒✉ ❦✐❫❡
✳♥ ❞✖❫❛
✒✉
y(−1) = 1
✳
HD gia
’i:
❱✐❫❡
✓t ♣❤✉✳♦✳♥❣ tr✏✒♥❤ ❧❛
✳✐✿
x(1 −y)y′=−2y
❀ ❞♦
y(−1) = 1
♥❫❡♥
y6≡ 0
✳ ❉
✲✉✳❛ ✈❫❡
✒
♣❤✉✳♦✳♥❣ tr✏✒♥❤ t❛✓❝❤ ❜✐❫❡
✓♥✿
1−y
ydy =−2dx
x
t✏✓❝❤ ♣❤❫❛♥ t❫♦
✬♥❣ q✉❛✓t✿
x2ye−y=C
✳ ❚❤❛② ❞✖✐❫❡
✒✉ ❦✐❫❡
✳♥ ✈❛✒♦ t❛ ❞✖✉✳♦✳
✳❝
C=1
e
✳ ❱❫❛
✳② t✏✓❝❤ ♣❤❫❛♥
r✐❫❡♥❣ ❝❫❛
✒♥ t✏✒♠ ❧❛✒✿
x2ye1−y= 1
✳
12)
❇✕❛
✒♥❣ ❝❛✓❝❤ ❞✖✕❛
✳t
y=ux
✱ ❤❛
⑦② ❣✐❛
✬✐ ♣❤✉✳♦✳♥❣ tr✏✒♥❤✿
xdy −ydx −px2−y2dx = 0.(x > 0)
HD gia
’i:
❉
✲✕❛
✳t
y=ux;du =udx +xdu
t❤❛② ✈❛✒♦ ♣❤✉✳♦✳♥❣ tr✏✒♥❤ ✈❛✒ ❣✐❛
✬♥ ✉✳✓♦✳❝
x
✿
xdu −
√1−u2dx = 0
✳ ❘♦
⑦r❛✒♥❣
u−±1
❧❛✒ ♥❣❤✐❫❡
✳♠✳ ❦❤✐
u6≡ ±1
❞✖✉✳❛ ♣❤✉✳♦✳♥❣ tr✏✒♥❤ ✈❫❡
✒t❛✓❝❤ ❜✐❫❡
✓♥✿
du
1−u2=dx
x
✳ ❚P❚◗✿
arcsin u−ln x=C
✭❞♦
x > 0
✮✳
❱❫❛
✳② ◆❚◗ ❝✉
✬❛ ♣❤✉✳♦✳♥❣ tr✏✒♥❤✿
y=±x; arcsin y
x= ln x+C
✳
13)
❚✏✒♠ ♥❣❤✐❫❡
✳♠ r✐❫❡♥❣ ❝✉
✬❛ ♣❤✉✳♦✳♥❣ tr✏✒♥❤✿
xy′=px2−y2+y
t❤♦❛
✬♠❛
⑦♥ ❞✖✐❫❡
✒✉ ❦✐❫❡
✳♥ ❞✖❫❛
✒✉
y(1) = 0
✳
HD gia
’i:
xy′=px2−y2+y⇐⇒ y′=r1−y2
x2+y
x
❞✖✕❛
✳t
u=y
x
❤❛②
y=ux
s✉② r❛
y′=xu′+u
♣❤✉✳♦✳♥❣ tr✏✒♥❤ t❤❛✒♥❤✿
xu′=√1−u2⇐⇒ du
√1−u2=dx
x
w w w .VNM ATH.com
4
⇐⇒ arcsin u= ln Cx
t❤♦❛
✬♠❛
⑦♥ ❞✖✐❫❡
✒✉ ❦✐❫❡
✳♥ ❞✖❫❛
✒✉
y(1) = 0
❦❤✐
C= 1
✳ ❱❫❛
✳② ♥❣❤✐❫❡
✳♠
y=±x
✳
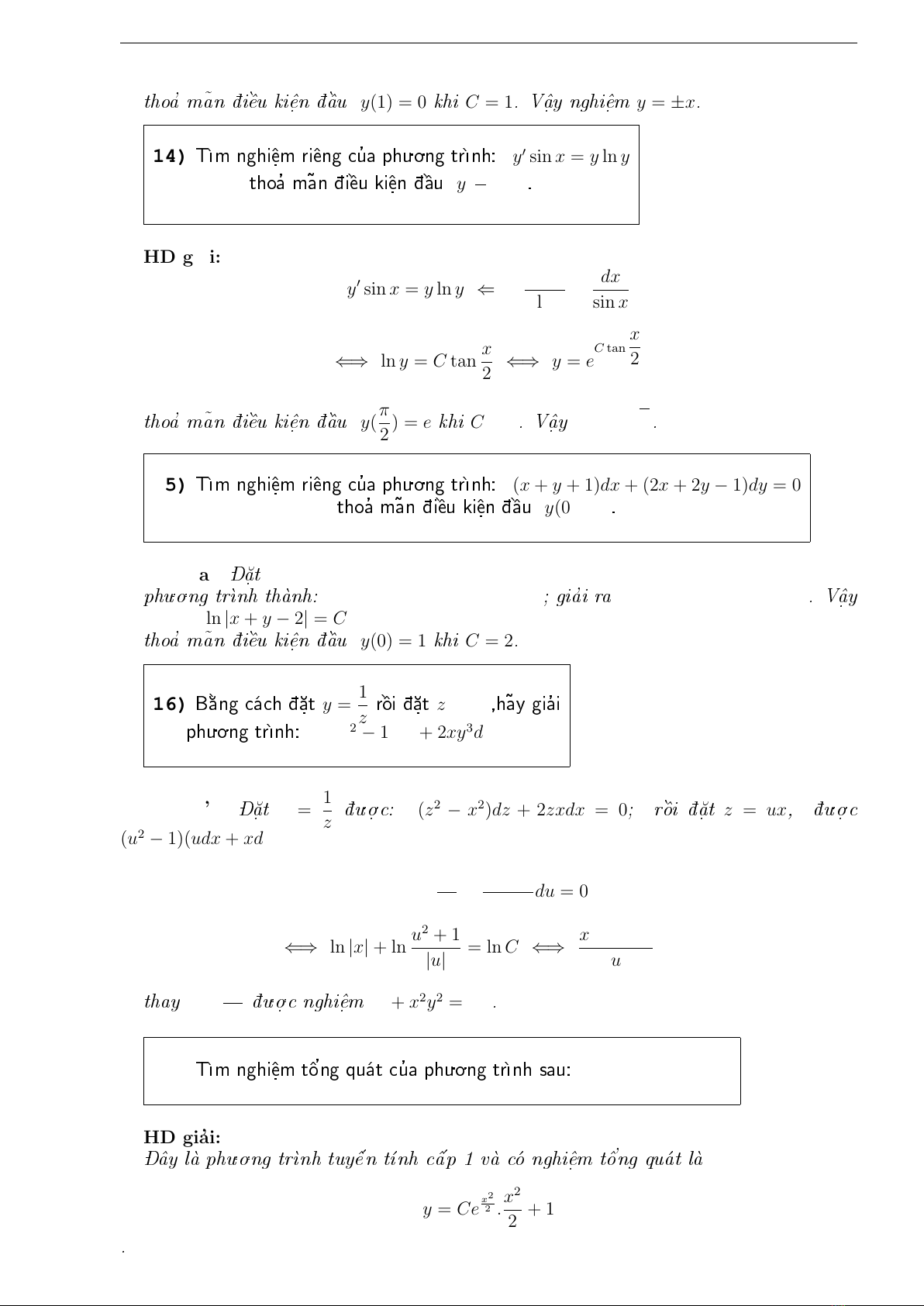
14)
❚✏✒♠ ♥❣❤✐❫❡
✳♠ r✐❫❡♥❣ ❝✉
✬❛ ♣❤✉✳♦✳♥❣ tr✏✒♥❤✿
y′sin x=yln y
t❤♦❛
✬♠❛
⑦♥ ❞✖✐❫❡
✒✉ ❦✐❫❡
✳♥ ❞✖❫❛
✒✉
y(π
2) = e
✳
HD gia
’i:
y′sin x=yln y⇐⇒ dy
yln y=dx
sin x
⇐⇒ ln y=Ctan x
2⇐⇒ y=eCtan x
2
t❤♦❛
✬♠❛
⑦♥ ❞✖✐❫❡
✒✉ ❦✐❫❡
✳♥ ❞✖❫❛
✒✉
y(π
2) = e
❦❤✐
C= 1
✳ ❱❫❛
✳②
y=etan x
2
✳
15)
❚✏✒♠ ♥❣❤✐❫❡
✳♠ r✐❫❡♥❣ ❝✉
✬❛ ♣❤✉✳♦✳♥❣ tr✏✒♥❤✿
(x+y+ 1)dx + (2x+ 2y−1)dy = 0
t❤♦❛
✬♠❛
⑦♥ ❞✖✐❫❡
✒✉ ❦✐❫❡
✳♥ ❞✖❫❛
✒✉
y(0) = 1
✳
HD gia
’i:
❉
✲✕❛
✳t
x+y=z=⇒dy =dz −dx
♣❤✉✳♦✳♥❣ tr✏✒♥❤ t❤❛✒♥❤✿
(2 −z)dx + (2z−1)dz = 0
❀ ❣✐❛
✬✐ r❛
x−2z−3 ln |z−2|=C
✳ ❱❫❛
✳②
x+ 2y+ 3 ln |x+y−2|=C
t❤♦❛
✬♠❛
⑦♥ ❞✖✐❫❡
✒✉ ❦✐❫❡
✳♥ ❞✖❫❛
✒✉
y(0) = 1
❦❤✐
C= 2
✳
16)
❇✕❛
✒♥❣ ❝❛✓❝❤ ❞✖✕❛
✳t
y=1
z
r❫♦
✒✐ ❞✖✕❛
✳t
z=ux
✱❤❛
⑦② ❣✐❛
✬✐
♣❤✉✳♦✳♥❣ tr✏✒♥❤✿
(x2y2−1)dy + 2xy3dx = 0
HD gia
’i:
❉
✲✕❛
✳t
y=1
z
❞✖✉✳♦✳
✳❝✿
(z2−x2)dz + 2zxdx = 0
❀ r❫♦
✒✐ ❞✖✕❛
✳t
z=ux
✱ ❞✖✉✳♦✳
✳❝
(u2−1)(udx +xdu) + 2udx = 0
⇐⇒ dx
x+u2−1
u3+udu = 0
⇐⇒ ln |x|+ ln u2+ 1
|u|= ln C⇐⇒ x(u2+ 1)
u=C
t❤❛②
u=1
xy
❞✖✉✳♦✳
✳❝ ♥❣❤✐❫❡
✳♠
1 + x2y2=Cy
✳
17)
❚✏✒♠ ♥❣❤✐❫❡
✳♠ t❫♦
✬♥❣ q✉❛✓t ❝✉
✬❛ ♣❤✉✳♦✳♥❣ tr✏✒♥❤ s❛✉✿
y′−xy =x+x3
HD gia
’i:
❉
✲❫❛② ❧❛✒ ♣❤✉✳♦✳♥❣ tr✏✒♥❤ t✉②❫❡
✓♥ t✏✓♥❤ ❝❫❛
✓♣ ✶ ✈❛✒ ❝♦✓ ♥❣❤✐❫❡
✳♠ t❫♦
✬♥❣ q✉❛✓t ❧❛✒
y=Cex2
2.x2
2+ 1
✳
w w w .VNM ATH.com

5
18)
❚✏✒♠ ♥❣❤✐❫❡
✳♠ t❫♦
✬♥❣ q✉❛✓t ❝✉
✬❛ ❝❛✓❝ ♣❤✉✳♦✳♥❣ tr✏✒♥❤ s❛✉✿
y′−y=y2.
HD gia
’i:
❉
✲❫❛② ❧❛✒ ♣❤✉✳♦✳♥❣ tr✏✒♥❤ t❛✓❝❤ ❜✐❫❡
✓♥ ✈❛✒ ❝♦✓ ♥❣❤✐❫❡
✳♠ t❫♦
✬♥❣ q✉❛✓t ❧❛✒
ln |y
y+ 1|=x+C.
19)
❚✏✒♠ ♥❣❤✐❫❡
✳♠ ❝✉
✬❛ ❝❛✓❝ ♣❤✉✳♦✳♥❣ tr✏✒♥❤ s❛✉✿
y′+y
x=ex
HD gia
’i:
❉
✲❫❛② ❧❛✒ ♣❤✉✳♦✳♥❣ tr✏✒♥❤ t✉②❫❡
✓♥ t✏✓♥❤ ❝❫❛
✓♣ ✶ ✈❛✒ ❝♦✓ ♥❣❤✐❫❡
✳♠ t❫♦
✬♥❣ q✉❛✓t ❧❛✒
y=C
x+ex−ex
x
✳
20)
❚✏✒♠ ♥❣❤✐❫❡
✳♠ ❝✉
✬❛ ❝❛✓❝ ♣❤✉✳♦✳♥❣ tr✏✒♥❤ s❛✉✿
y′−y=y3.
HD gia
’i:
❉
✲❫❛② ❧❛✒ ♣❤✉✳♦✳♥❣ tr✏✒♥❤ t❛✓❝❤ ❜✐❫❡
✓♥ ✈❛✒ ❝♦✓ ♥❣❤✐❫❡
✳♠ t❫♦
✬♥❣ q✉❛✓t ❧❛✒
C+x= ln |y| − arctgy.
21)
●✐❛
✬✐ ♣❤✉✳♦✳♥❣ tr✏✒♥❤✿
y′=y
x+ sin y
x
✱ ✈✓♦✳✐
y(1) = π
2
HD gia
’i: y=zx ⇒y′=z′x+z
✱ ♣❤✉✳♦✳♥❣ tr✏✒♥❤ tr♦✳
✬t❤❛✒♥❤✿
z′x= sin x⇔dz
sin z=dx
x⇔ln |tg z
2|= ln |x|+ ln C⇔tg z
2=Cx
❱❫❛
✳② ♥❣❤✐❫❡
✳♠ t❫♦
✬♥❣ q✉❛✓t✿
tg y
2x=Cx;y(1) = π
2⇒C= 1.
❱❫❛
✳②✿
tg y
2x=x
✳
22)
●✐❛
✬✐ ♣❤✉✳♦✳♥❣ tr✏✒♥❤✿
(x−ycos y
x)dx +xcos y
xdy = 0
HD gia
’i:
❉
✲✕❛
✳t
y
x=z⇒y′=z′x+z
♣❤✉✳♦✳♥❣ tr✏✒♥❤ ❞✖✉✳♦✳
✳❝ ❞✖✉✳❛ ✈❫❡
✒❞❛
✳♥❣✿
xcos z.z′+ 1 = 0 ⇔Zcos zdz =−dx
x+C⇔sin z=−ln |x|+C
❱❫❛
✳② ❚P❚◗✿
sin y
x=−ln |x|+C
23)
●✐❛
✬✐ ♣❤✉✳♦✳♥❣ tr✏✒♥❤✿
(y′2−1)x2y2+y′(x4−y4) = 0
HD gia
’i:
▲❛✒ ♣❤✉✳♦✳♥❣ tr✏✒♥❤ ❞✖✕❛
✬♥❣ ❝❫❛
✓♣ ♥❤✉✳♥❣ ❣✐❛
✬✐ ❦❤❛✓ ♣❤✓✉✳❝ t❛
✳♣✳
w w w .VNM ATH.com


















![Giáo trình Giải tích hàm một biến 1: Phần 2 [Full Nội Dung]](https://cdn.tailieu.vn/images/document/thumbnail/2026/20260127/hoatulip0906/135x160/60731769587731.jpg)
![Giáo trình Giải tích hàm một biến 1: Phần 1 [Full]](https://cdn.tailieu.vn/images/document/thumbnail/2026/20260127/hoatulip0906/135x160/70271769587732.jpg)



![Bài tập Toán cao cấp (HP1) [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2026/20260127/hoahongcam0906/135x160/69221769507713.jpg)


