
Tư duy mở trắc nghiệm toán lý
Sưu tầm và tổng hợp
(Đề thi có 87 trang)
700 CÂU VD TÍCH PHÂN
Môn: Toán
Thời gian làm bài phút (700 câu trắc nghiệm)
Họ và tên thí sinh: .................................................... Mã đề thi 616
Câu 1. Cho hàm số f(x)liên tục trên Rthỏa mãn
π
4
Z
0
f(tan x) dx= 3 và
1
Z
0
x2f(x)
x2+ 1 dx= 1. Tính
I=
1
Z
0
f(x) dx.
AI= 3.BI= 2.CI= 6.DI= 4.
Câu 2. Cho hàm số y=f(x)thỏa mãn
1
Z
0
f(x) dx= 1 và
3
Z
1
f(x) dx= 8. Tính tích phân
I=
3
Z
1
f(|2x−5|) dx.
AI=−8.BI=−6.CI= 5.DI=−4.
Câu 3. Xét
ln 2
Z
0
√ex−1 dx. Nếu đặt u=√ex−1thì
ln 2
Z
0
√ex−1 dxbằng
A
1
Z
0
1
udu.B
1
Z
0
udu.C
1
Z
0
u
u2+ 1 du.D
1
Z
0
√udu.
Câu 4.
Cho hình (H)giới hạn bởi đồ thị hàm số y=√3
9x3, cung
tròn có phương trình y=√4−x2(với 0≤x≤2) và trục
hoành (phần tô đậm trong hình vẽ). Biết thể tích của khối
tròn xoay tạo thành khi quay (H)quanh trục hoành là V=
−a
b√3 + c
dπ, trong đó a, b, c, d ∈N∗và a
b,c
dlà các phân
số tối giản. Tính P=a+b+c+d.
AP= 34.BP= 52.CP= 46.DP= 40.x
y
O2
2
Câu 5. Cho hàm số f(x)liên tục trên đoạn [−2; 2] và là hàm số chẵn. Biết
1
Z
0
f(2x) dx= 4. Tính
I=
2
Z
−2
f(x) dx.
AI= 8.BI= 16.CI= 4.DI= 2.
Câu 6. Tính thể tích Vcủa vật tròn xoay tạo thành khi quay hình phẳng (H)giới hạn bởi các
đường y=x2;y=√xquanh trục Ox.
AV=7π
10 .BV=π
10.CV=9π
10 .DV=3π
10 .
Trang 1/87 −Mã đề 616
Câu 7. Biết
5
Z
2
dx
x2−x=aln 4 + bln 2 + cln 5,với a,b,clà 3số nguyên khác 0. Tính P=
a2+ 2ab + 3b2−2c.
A7.B8.C4.D5.
Câu 8. Trong không gian Oxyz cho ba điểm A(1; 2 −4),B(1; −3; 1),C(2; 2; 3). Mặt cầu (S)đi
qua A,B,Cvà có tâm thuộc mặt phẳng (Oxy). Khi đó bán kính mặt cầu (S)là
A2.B3√2.C5.D√26.
Câu 9. Tính thể tích vật thể tròn xoay tạo bởi phép quay xung quanh trục Ox hình phẳng giới
hạn bởi các đường y= 0, y =√x, y =x−2.
A10π.B8π.C16π
3.D8π
3.
Câu 10. Một ô-tô bắt đầu chuyển động nhanh dần đều với vận tốc v1(t) = 7t(m/s). Đi được 5
(s), người lái xe phát hiện chướng ngại vật và phanh gấp, ô-tô tiếp tục chuyển động chậm dần
đều với gia tốc a=−70 (m/s2). Tính quãng đường S(m) đi được của ô-tô từ lúc bắt đầu chuyển
bánh cho đến khi dừng hẳn.
AS= 94,00 (m). BS= 87,50 (m). CS= 96,25 (m). DS= 95,70 (m).
Câu 11. Cho hàm số f(x)có đạo hàm dương và liên tục trên R+, thỏa mãn điều kiện f(1) = 3
và ln f′(x)
2x+f(x) = x2+ 2,∀x∈R+. Tính f(3).
A2 + ln 3.B1.C3 + ln 2.D11.
Câu 12. Cho hàm số f(x)liên tục trên Rvà f(2) = 16,
2
Z
0
f(x) dx= 4. Tính I=
4
Z
0
xf′x
2dx.
AI= 28.BI= 144.CI= 12.DI= 112.
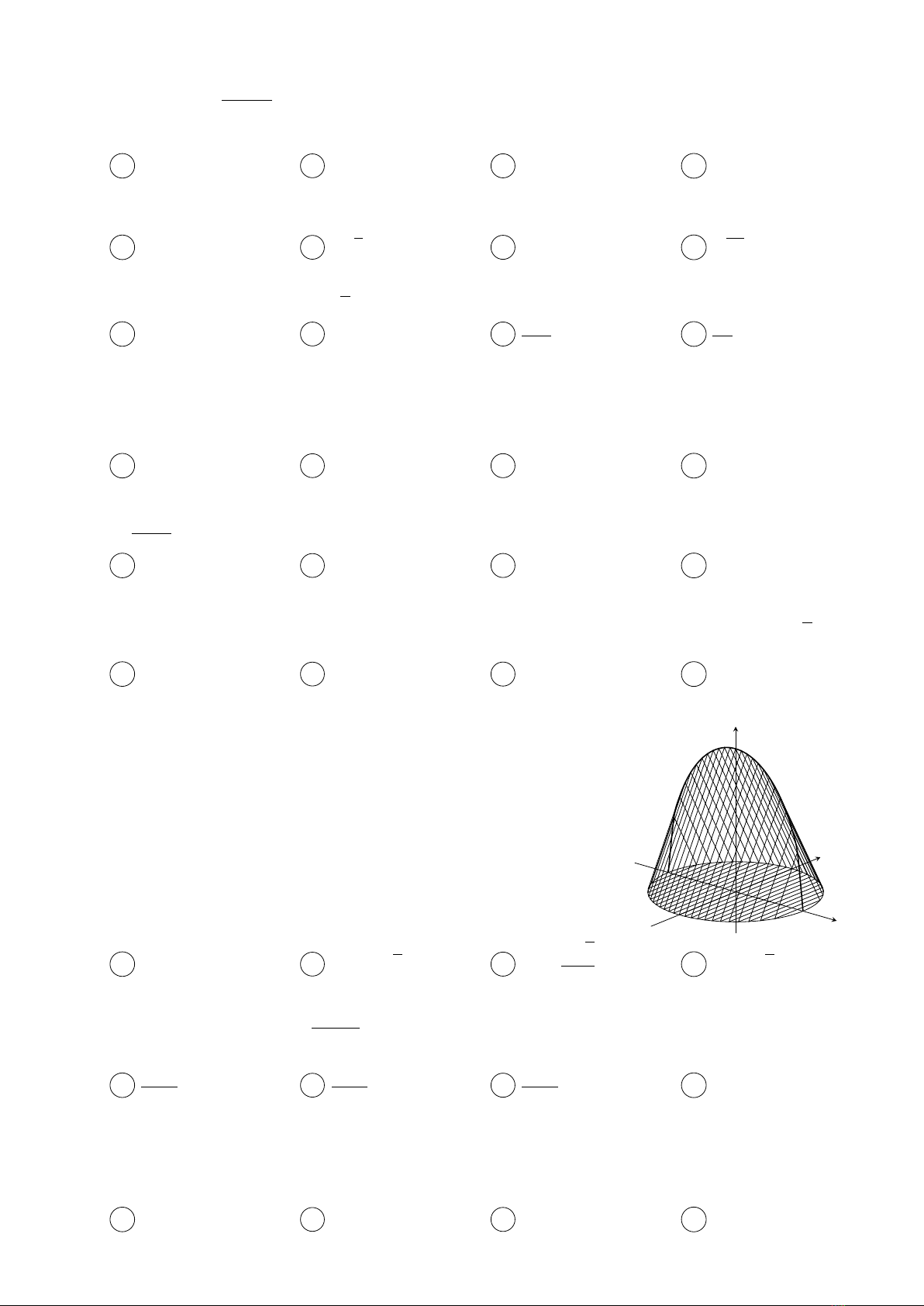
Câu 13.
Cho vật thể có mặt đáy là hình tròn có bán kính bằng 1(hình vẽ).
Khi cắt vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có
hoành độ x(−1≤x≤1) thì được thiết diện là một tam giác đều.
Tính thể tích Vcủa vật thể đó.
x
y
z
AV=π.BV= 3√3.CV=4√3
3.DV=√3.
Câu 14. Tích phân I=
2
Z
−2
x2020
ex+ 1dxcó giá trị bằng
A22021
2021.B22022
2022.C22022
2021.D0.
Câu 15. Cho hàm số y=f(x)liên tục trên đoạn [0; 1] và
1
Z
0
xf′(x) dx=a. Tính
1
Z
0
f(x) dxtheo
avà b=f(1).
Aa+b.B−a−b.Cb−a.Da−c.
Trang 2/87 −Mã đề 616
Câu 16. Gọi Slà diện tích hình phẳng giói hạn bởi đồ thị của hàm số (P): y=x2−4x+ 3 và
các tiếp tuyến kẻ từ điểm A3
2;−3đến đồ thị (P). Giá trị của Sbằng
A9.B9
2.C9
8.D9
4.
Câu 17. Biết
2
Z
−2
x+ 1
x2−9dx=−a
bln 5 với a, b ∈Nvà a
blà phân số tối giản. Tính giá trị a+b.
A8.B7.C10.D4.
Câu 18. Cho hàm số f(x)liên tục trên R. Biết F(x) = x2
2−1sin x+xcos xlà một nguyên
hàm của hàm số f(x) cos x, họ tất cả các nguyên hàm của hàm số f′(x) sin xlà
Axsin x+ cos x+C.Bxsin x+xcos x+C.
Csin x−xcos x+C.Dsin x+xcos x+C.
Câu 19. Tìm tất cả các giá trị thực của tham số kđể có
k
Z
1
(2x−1)dx = 4 lim
x→0
√x+ 1 −1
x.
A"k= 1
k= 2.B"k=−1
k= 2 .C"k=−1
k=−2.D"k= 1
k=−2.
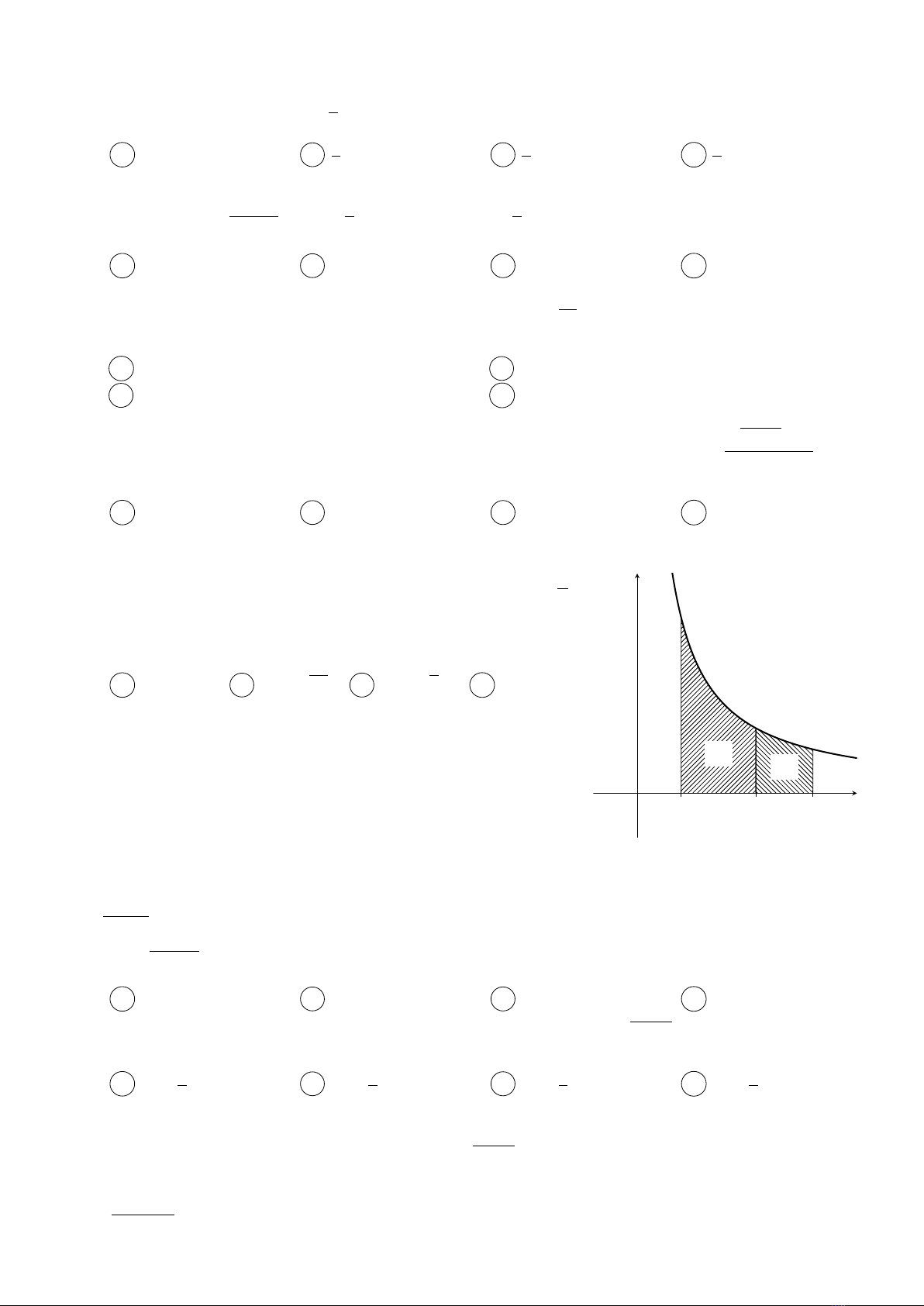
Câu 20.
Cho hình thang cong (H)giới hạn bởi các đường y=1
x,
y= 0,x= 1,x= 5. Đường thẳng x=k,1< k < 5chia (H)
thành hai phần có diện tích S1và S2(hình vẽ bên). Giá trị k
để S1= 2S2là
Ak= 5.Bk=3
√25.Ck=3
√5.Dk= ln 5.
5
k
1
0x
y
S1S2
Câu 21. Cho hàm số f(x)liên tục trên Rthỏa mãn
2018
Z
0
f(x) dx= 2. Khi đó giá trị tích phân
√e2018−1
Z
0
x
x2+ 1flnx2+ 1dxbằng
A4.B1.C2.D3.
Câu 22. Cho hình (H)là hình phẳng giới hạn bởi các đường y=√x+ 1, y = 1 −xvà trục Ox.
Diện tích Scủa hình (H)bằng bao nhiêu?
AS=7
6.BS=3
2.CS=5
4.DS=4
3.
Câu 23. Cho hàm số y=f(x)thỏa mãn
1
Z
0
f′(x)
x+ 1 dx= 1 và f(1) −2f(0) = 2. Tính I=
1
Z
0
f(x)
(x+ 1)2dx.
Trang 3/87 −Mã đề 616
AI= 3.BI= 1.CI=−1.DI= 0.
Câu 24. Cho F(x)là nguyên hàm của hàm số f(x) = x2+x+ 1
x+ 1 và F(0) = 2018. Tính F(−2).
AF(−2) = 2018.BF(−2) không xác định.
CF(−2) = 2020.DF(−2) = 2.
Câu 25. Tính diện tích hình phẳng giới hạn bởi các đường y=x2−4x+ 3; y= 0; x= 0 và
x= 4.
A4
3.B4.C3
4.D1
4.
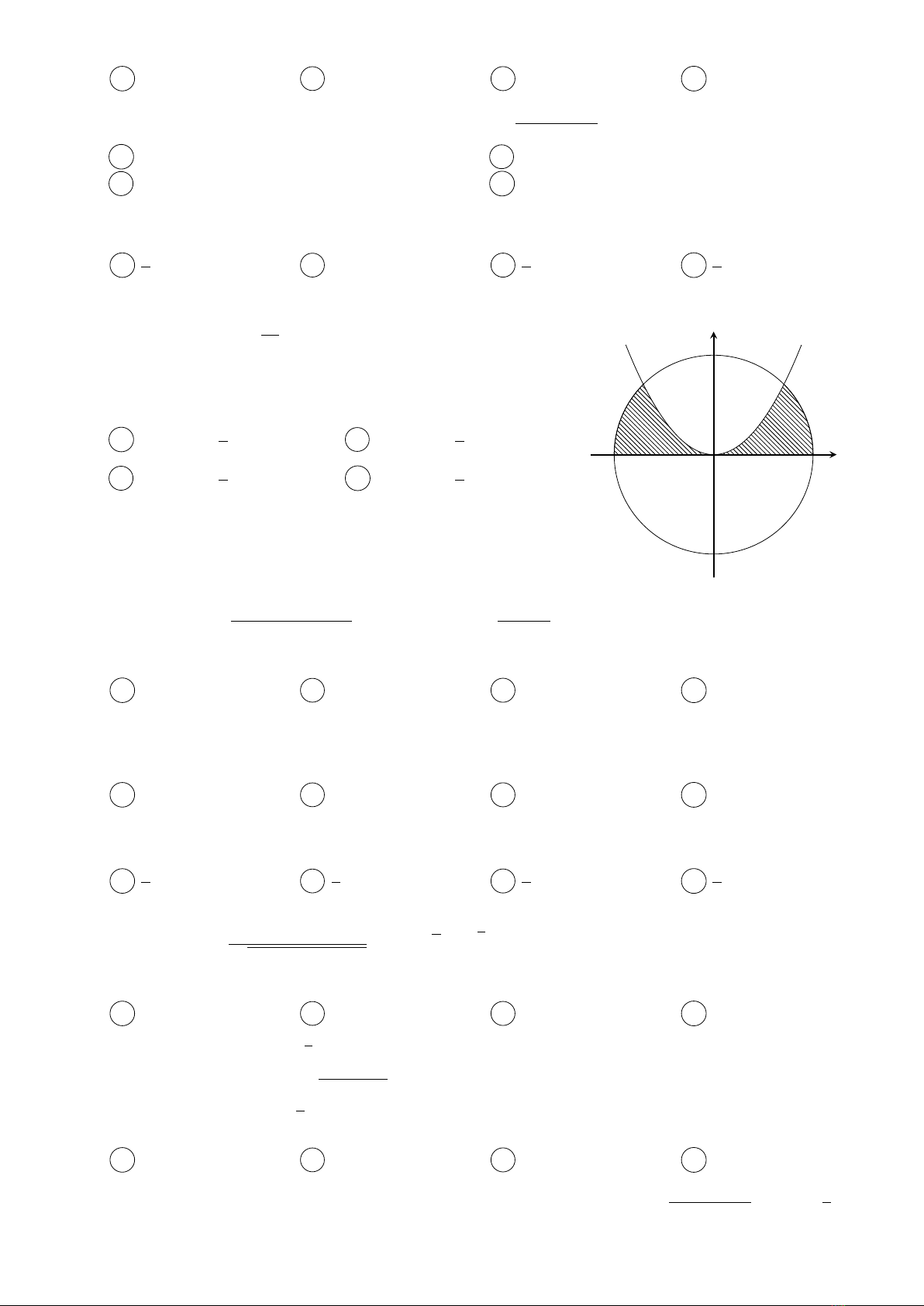
Câu 26.
Cho Parabol (P):y=x2
2và đường tròn (C) : x2+y2= 8. Gọi
(H)là phần hình phẳng giới hạn bởi (P),(C)và trục hoành
(phần tô đậm như hình vẽ bên). Tính diện tích S của hình
phẳng (H).
AS= 2π+4
3.BS= 2π−2
3.
CS= 2π+1
3.DS= 2π−4
3.O
x
y
Câu 27. Biết
1
Z
0
(x2+ 5x+ 6)ex
x+ 2 + e−xdx=a.e−b−ln a.e + c
3với a, b, c là các số nguyên và elà cơ
số của logarit tự nhiên. Tính S= 2a+b+c.
AS= 10.BS= 9.CS= 0.DS= 0.
Câu 28. Giá trị của tích phân
100
Z
0
x(x−1) ···(x−100)dxbằng
A100.B1.Cmột giá trị khác. D0.
Câu 29. Cho parabol (P) : y=x2và hai điểm A,Bthuộc (P)sao cho AB = 2. Tìm giá trị lớn
nhất của diện tích hình phẳng giới hạn bởi parabol (P)và đường thẳng AB.
A3
2.B4
3.C3
4.D5
6.
Câu 30. Cho
1
Z
0
1
p(x+ 3)(x+ 1)3dx=√a−√bvới a, b là các số nguyên. Giá trị của biểu thức
ab+babằng
A32.B17.C145.D57.
Câu 31. Cho tích phân
π
2
Z
π
3
sin x
cos x+ 2 dx=aln 5 + bln 2 với a, b ∈Z. Mệnh đề nào sau đây
đúng?
Aa−2b= 0.Ba+ 2b= 0.C2a+b= 0.D2a−b= 0.
Câu 32. Cho hàm số f(x)xác định trên R\ {−2; 1}thoả mãn f′(x) = 1
x2+x−2, f(0) = 1
3và
f(−3) −f(3) = 0. Tính giá trị của biểu thức T=f(−4) + f(−1) −f(4).
Trang 4/87 −Mã đề 616

A1
3ln 2 + 1
3.B1
3ln 4
5+ ln 2 + 1.
Cln 80 + 1.D1
3ln 8
5+ 1.
Câu 33. Cho hàm số f(x)6= 0 thỏa mãn điều kiện f′(x) = (2x+ 3)f2(x)và f(0) = −1
2. Biết
rằng tổng f(1) + f(2) + f(3) + ··· +f(2017) + f(2018) = a
bvới (a∈Z, b ∈N∗)và a
blà phân số
tối giản. Mệnh đề nào sau đây đúng?
Aa
b<−1.Bb−a= 3029.Ca
b>1.Da+b= 1010.
Câu 34. Cho tích phân
3
Z
2
1
x3+x2dx=aln 3 + bln 2 + c, với a, b, c ∈Q. Tính S=a+b+c.
AS=−2
3.BS=7
6.CS=−7
6.DS=2
3.
Câu 35.
Cho hàm số y=f(x)xác định và liên tục trên đoạn [−3; 3]. Biết rằng
diện tích hình phẳng S1,S2giới hạn bởi đồ thị hàm số y=f(x)
với đường thẳng y=−x−1lần lượt là M,m. Tính tích phân
3
Z
−3
f(x) dx.
A6 + m−M.Bm−M−6.
C6−m−M.DM−m+ 6.
x
y
1 3
−3
−4
2
−2
0
−1
−6
S1S2
Câu 36. Biết
1
Z
0
1
x2+ 3x+ 2 dx=aln 2 + bln 3 với a,blà các số hữu tỉ. Hỏi a+bbằng bao
nhiêu?
A3.B4.C1.D2.
Câu 37. Cho hàm số f(x)liên tục trên R. Biết ln xlà một nguyên hàm của hàm số xf(x),họ
tất cả các nguyên hàm của hàm số f′(x) ln xlà
Aln x
x2−1
2x2+C.Bln x
x+1
2x2+C.Cln x
x2+1
x+C.Dln x
x2+1
2x2+C.
Câu 38. Cho
e
Z
1
ln x
√xdx=a√e + bvới a, b là các số hữu tỉ. Tính P=a·b.
AP= 8.BP=−4.CP= 4.DP=−8.
Câu 39.
Tính diện tích hình phẳng giới hạn bởi nửa đường tròn y=√2−x2,
đường thẳng AB biết A(−√2; 0),B(1; 1) (phần tô đậm như hình vẽ).
Aπ−2√2
4.B3π−2√2
4.C3π+ 2√2
4.Dπ+√2
4.x
y
−√2
A
1
O
B
Câu 40. Cho f(x)là hàm số chẵn, liên tục trên Rthoả mãn
1
Z
0
f(x) dx= 2018 và g(x)là hàm
Trang 5/87 −Mã đề 616





![Bài tập so sánh hơn và so sánh nhất của tính từ [kèm đáp án/mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250808/nhatlinhluong27@gmail.com/135x160/77671754900604.jpg)
![Tài liệu tham khảo Tiếng Anh lớp 8 [mới nhất/hay nhất/chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250806/anhvan.knndl.htc@gmail.com/135x160/54311754535084.jpg)




![Tài liệu Lý thuyết và Bài tập Tiếng Anh lớp 6 [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250802/hoihoangdang@gmail.com/135x160/18041754292798.jpg)




