
An toàn và An ninh thông tin
Nguyễn Linh Giang
BộmônTruyền thông
vàMạng máytính
I. Nhập môn An toàn thông tin
II. Các phương pháp mã hóa đốixứng
III. Các hệmật khóa công khai
IV. Xác thực thông điệp
V. Chữký sốvà các giao thứcxácthực
VI. Đánh dấuẩnvàodữliệu
Chương II.
Các phương pháp mã hóa đốixứng
1. Sơđồchung củaphương phápmãhóa
đốixứng
2. Mộtsốphương phápmãhóađốixứng
kinh điển
3. Phương phápDES
4. Quảntrịvàphânphốikhóa
zGiảthiết
–Thuậttoánmãhóaphảiđủ mạnh để không thểgiải
mãđượcthông điệpnếuchỉdựatrênduynhấtnội
dung củavănbảnđượcmãhóa( ciphertext ).
–Sựan toàncủaphương phápmãhóađốixứng chỉ
phụthuộcvàođộ bímậtcủakhóamàkhông phụ
thuộcvàođộ bímậtcủathuậttoán.
Sơđồmãhóađốixứng
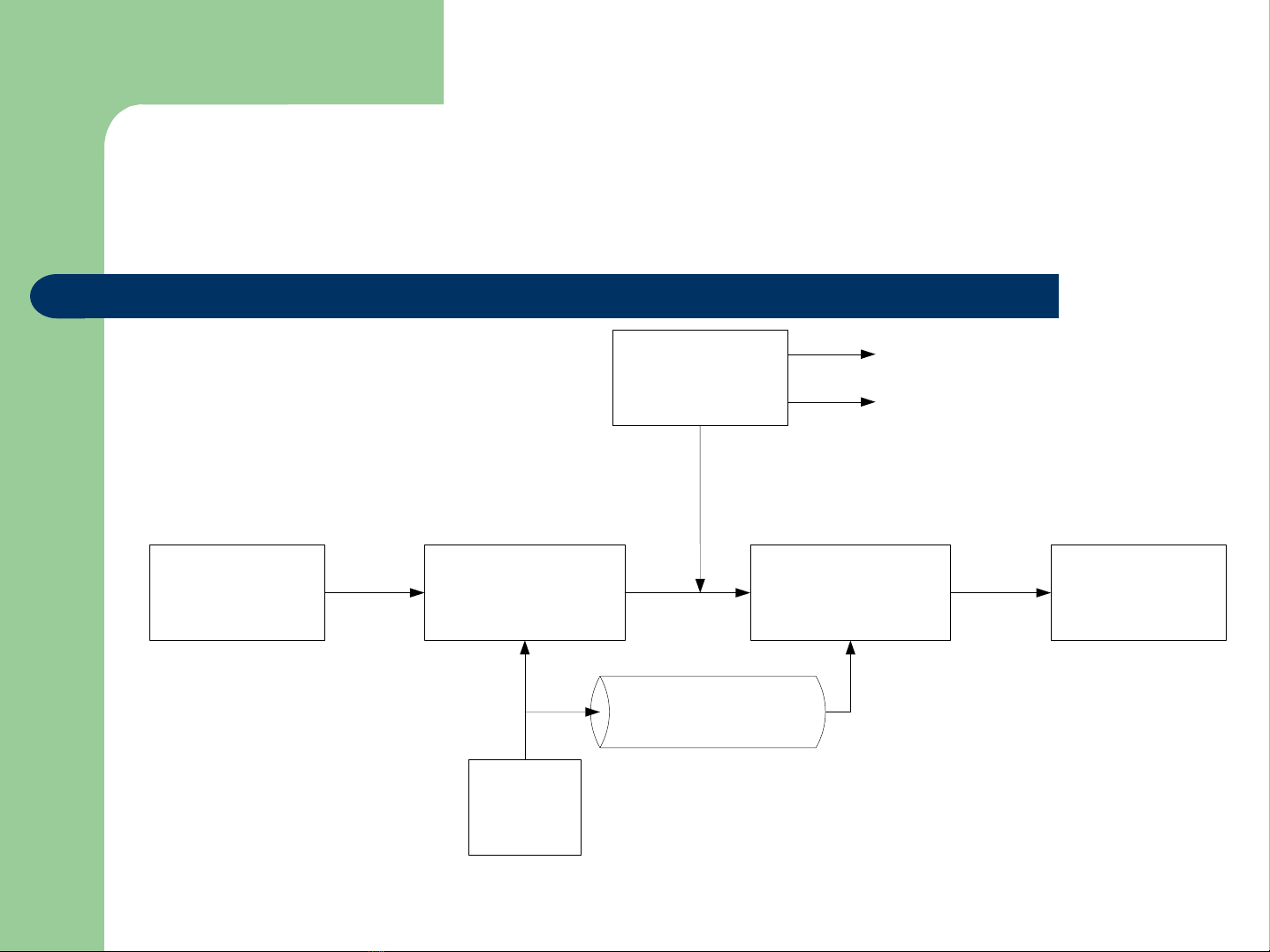
Môhình hệthống mãhóađốixứng.
Nguån th«ng
®iÖp Khèi m· hãa Khèi gi¶i m· Nguån th«ng
®iÖp
Khãa
mËt
Th¸m m·
Kªnh mËt
XY X
K
X
*
K
*
Sơđồmãhóađốixứng


























