intTypePromotion=1
zunia.vn Tuyển sinh 2024 dành cho Gen-Z zunia.vn zunia.vn
ADSENSE
 » 
 » 

Bài giảng Cơ học ứng dụng: Tuần 2 - Nguyễn Duy Khương

Chia sẻ: Thiên Lăng Sở | Ngày: | Loại File: PDF | Số trang:17

Thêm vào BST
Báo xấu
24
lượt xem 2
download
 
  Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng Cơ học ứng dụng: Tuần 2 - Nguyễn Duy Khương cung cấp cho học viên những kiến thức về thu gọn hệ lực, điều kiện cân bằng; bất biến của hệ lực; định lý tương đương cơ bản; điều kiện cân bằng của hệ; hệ lực đặc biệt;... Mời các bạn cùng tham khảo chi tiết nội dung bài giảng!

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Cơ học ứng dụng: Tuần 2 - Nguyễn Duy Khương

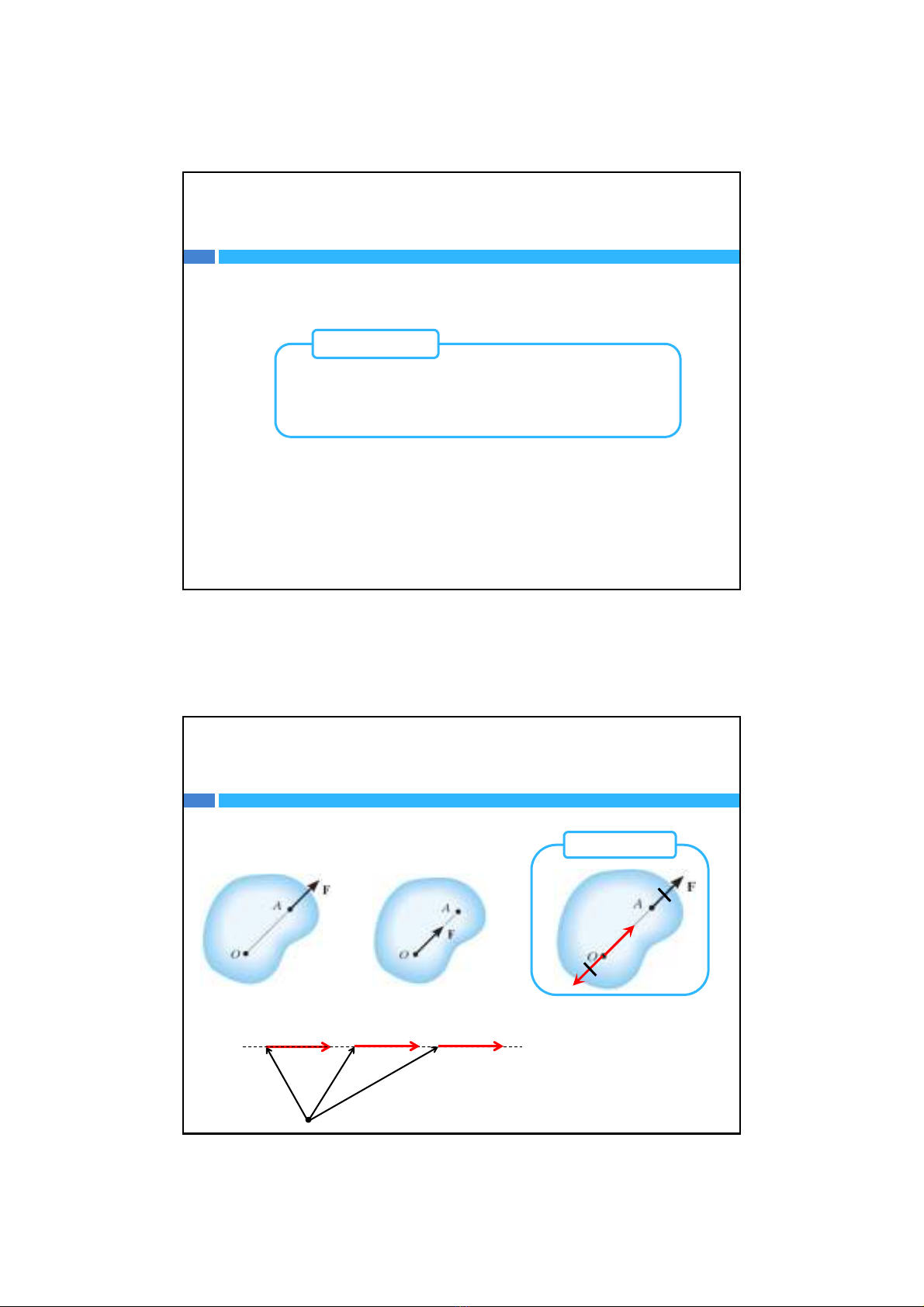
  1. Khoa Khoa Học Ứng Dụng 9/7/2011 Bài giảng Cơ Học Ứng Dụng - Tuần 2 CHƯƠNG 2 Thu gọn hệ lực, điều kiện cân bằng NỘI DUNG 1. Định lý tương đương cơ bản 2. Điều kiện cân bằng của hệ CHƯƠNG 2 Thu gọn hệ lực, điều kiện cân bằng 1. Định lý tương đương cơ bản Định lý dời lực: 1.Dời lực trên đường tác dụng của lực Chứng minh  F ‐F Lực trượt trên đường tác dụng của nó thì hệ không thay đổi. F F F r1 r2 r3        M O ( F )  r1  F  r2  F  r3  F O Giảng viên Nguyễn Duy Khương 1
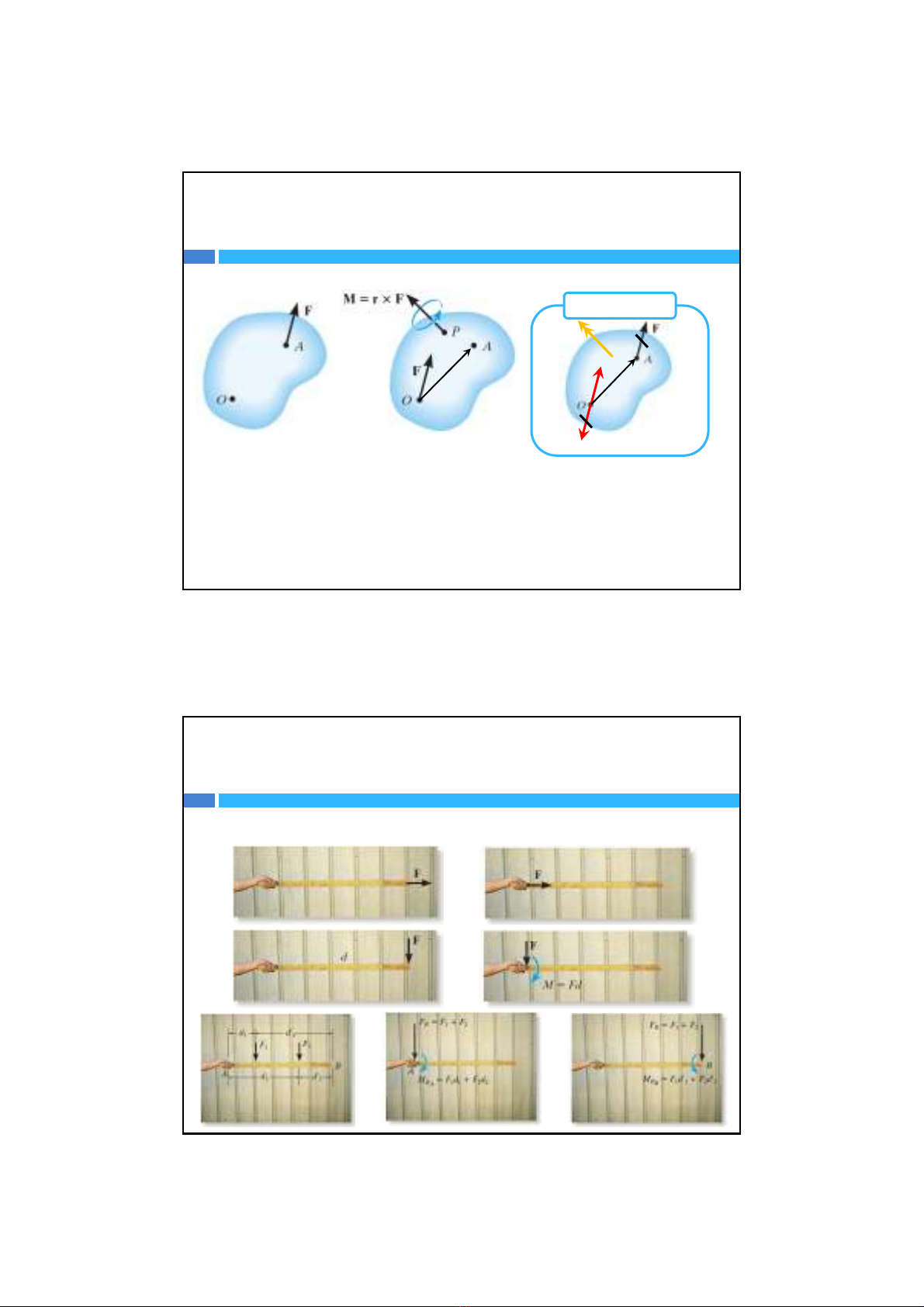
  2. Khoa Khoa Học Ứng Dụng 9/7/2011 Bài giảng Cơ Học Ứng Dụng - Tuần 2 CHƯƠNG 2 Thu gọn hệ lực, điều kiện cân bằng 1. Định lý tương đương cơ bản 2.Dời lực không trên đường tác dụng của lực Chứng minh  r F r ‐F    Lực không trượt trên giá của nó sẽ sinh ra Moment M  rF Momen có điểm đặt tự do, có thể ở P, O, A hoặc bất kì đâu Moment không phụ thuộc điểm đặt CHƯƠNG 2 Thu gọn hệ lực, điều kiện cân bằng 1. Định lý tương đương cơ bản Thực hành dời lực     Giảng viên Nguyễn Duy Khương 2
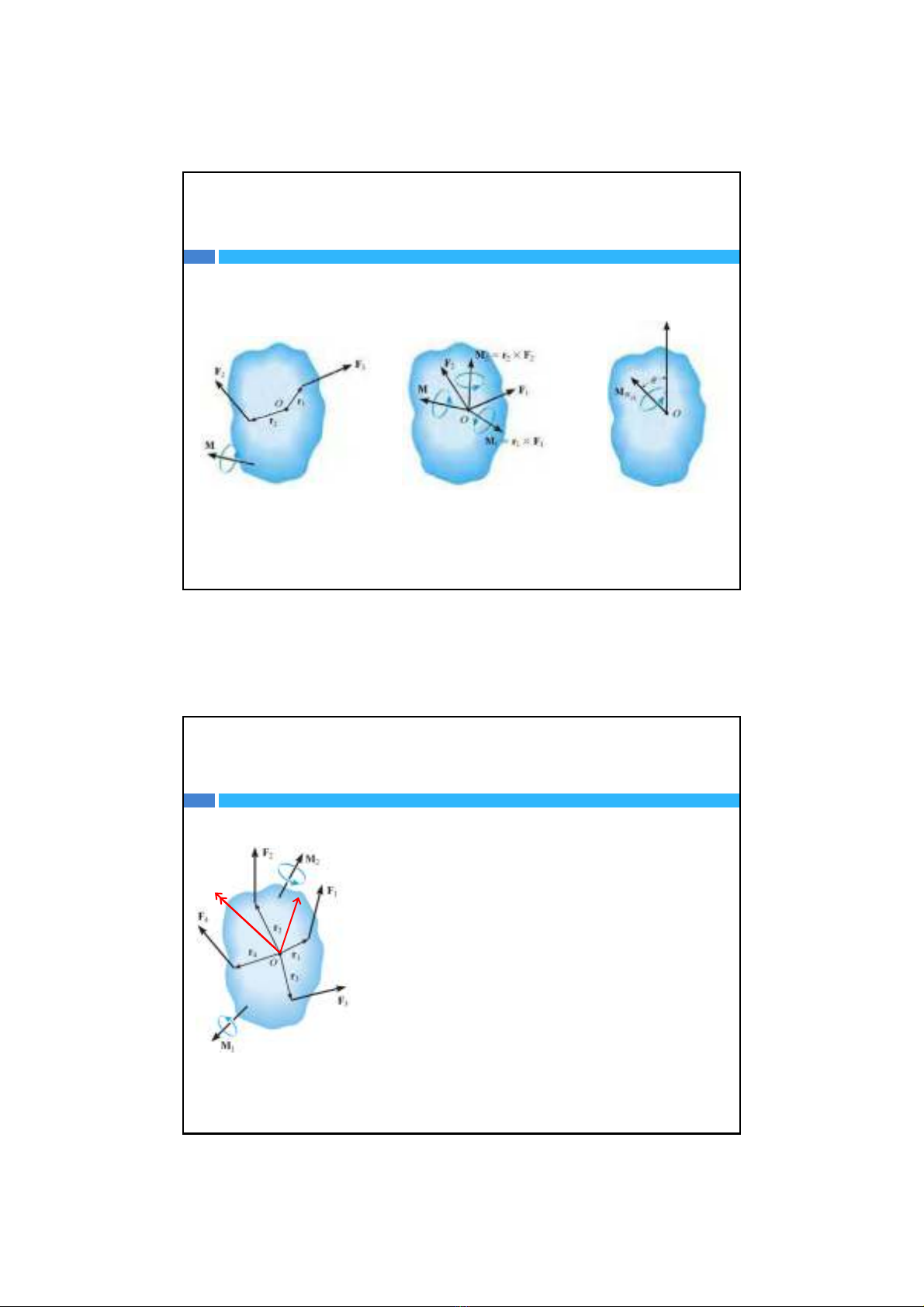
  3. Khoa Khoa Học Ứng Dụng 9/7/2011 Bài giảng Cơ Học Ứng Dụng - Tuần 2 CHƯƠNG 2 Thu gọn hệ lực, điều kiện cân bằng 1. Định lý tương đương cơ bản R = = CHƯƠNG 2 Thu gọn hệ lực, điều kiện cân bằng 1. Định lý tương đương cơ bản Thu gọn hệ lực về một điểm tương với một vector chính và một vector moment chính (phương pháp giải tích)  M RO  Vector chính: R   R   Fi Với Fi là các lực thành phần Vector moment chính:     M RO   M O ( F i )  M j Với Mj là các moment thành phần MO(Fi) là các moment do các lực thành phần đối với tâm O Giảng viên Nguyễn Duy Khương 3
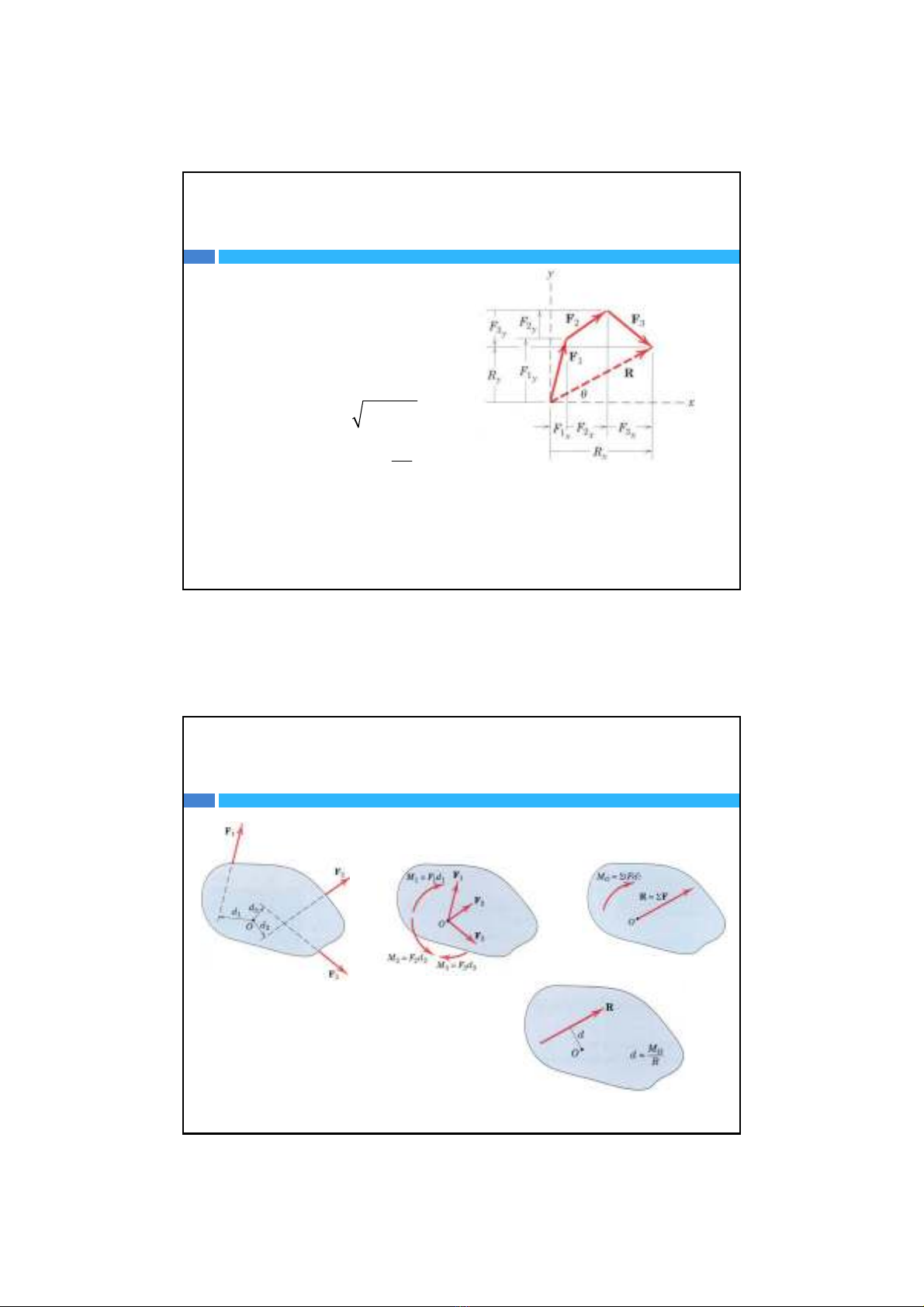
  4. Khoa Khoa Học Ứng Dụng 9/7/2011 Bài giảng Cơ Học Ứng Dụng - Tuần 2 CHƯƠNG 2 Thu gọn hệ lực, điều kiện cân bằng 1. Định lý tương đương cơ bản Hợp lực trong mặt phẳng (phương pháp đại số) Vector chính:      R  F1  F2  F3  ...   Fi Với: Rx   Fix Ry   Fiy R  Rx2  Ry2 Ry   tan 1 Rx Là góc hợp bởi hợp lực và phương ngang CHƯƠNG 2 Thu gọn hệ lực, điều kiện cân bằng 1. Định lý tương đương cơ bản = = Ta có thể dời hợp lực đến một điểm nào đó chỉ có lực chính mà không có moment  chính không? Chỉ còn một lực duy nhất !! Giảng viên Nguyễn Duy Khương 4
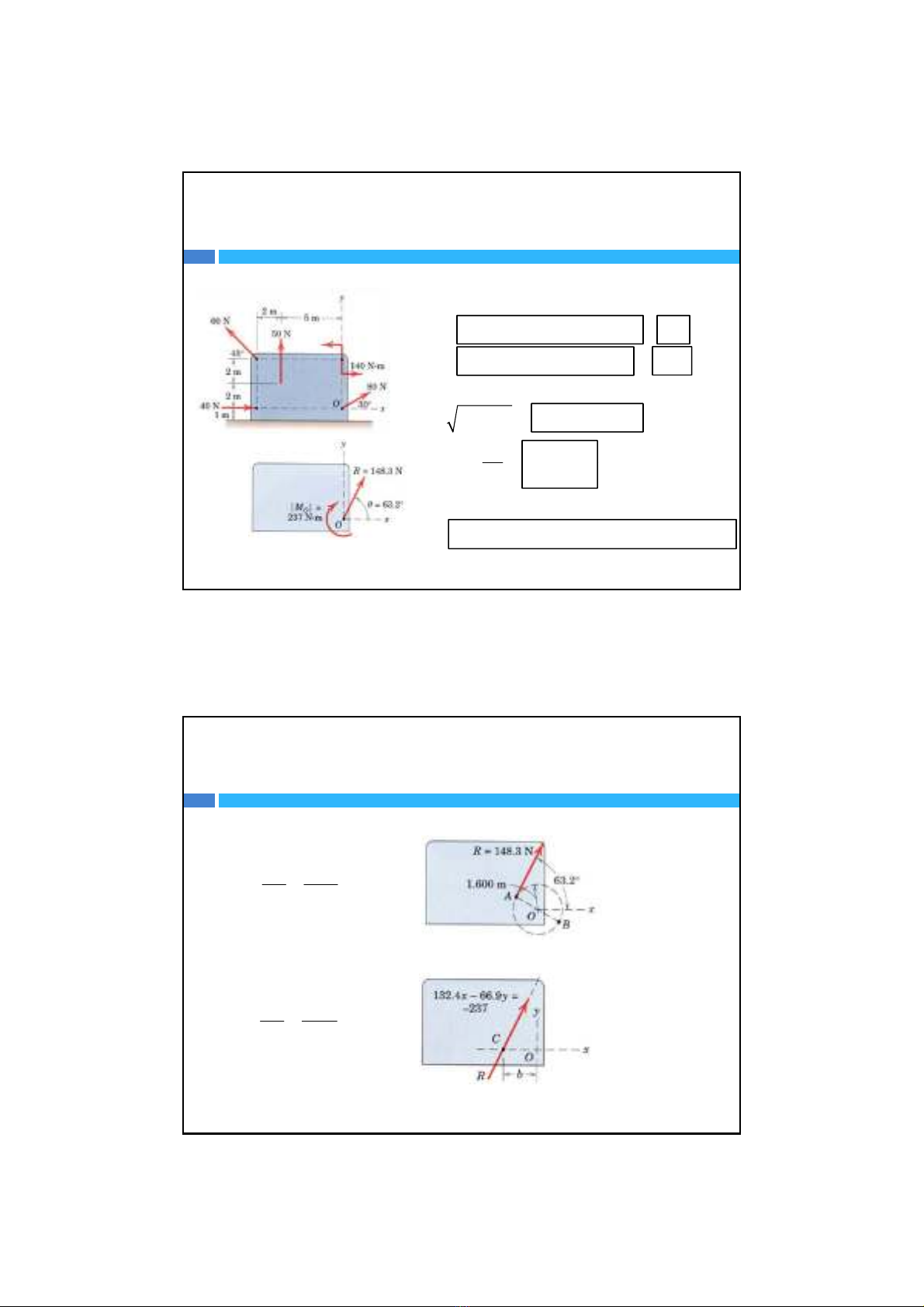
  5. Khoa Khoa Học Ứng Dụng 9/7/2011 Bài giảng Cơ Học Ứng Dụng - Tuần 2 CHƯƠNG 2 Thu gọn hệ lực, điều kiện cân bằng 1. Định lý tương đương cơ bản Ví dụ 1: Thu gọn hệ lực về tâm O (phương pháp đại số) Lực chính theo phương x và y Rx  40  80 cos 30o  60 cos 45o  66,9 N Ry  50  80sin 30o  60sin 45o  132, 4 N Lực chính tổng là: R  Rx2  Ry2  66,92  132, 42  148,3 N Ry 132, 4   tan 1  tan 1  63, 2o Rx 66,9 Moment tổng tại O M O  140  50(5)  60 cos 45o (4)  60sin 45o (7)  237 N  m CHƯƠNG 2 Thu gọn hệ lực, điều kiện cân bằng 1. Định lý tương đương cơ bản Điểm đặt của lực chính để hệ không còn moment chính là MO 237 d= = = 1, 6m R 148,3 Điểm đặt của lực chính nằm trên Ox cách O một khoảng b là MO 237 b= = = 1, 792m Ry 132, 4 Giảng viên Nguyễn Duy Khương 5
  6. Khoa Khoa Học Ứng Dụng 9/7/2011 Bài giảng Cơ Học Ứng Dụng - Tuần 2 CHƯƠNG 2 Thu gọn hệ lực, điều kiện cân bằng 1. Định lý tương đương cơ bản Ví dụ 2: Thu gọn hệ lực về tâm A (phương pháp giải tích)  F1  100i  (100, 0)  F2  600 j  (0, 600)  F3  200 2i  200 2 j  (282.9, 282.9) Vector chính:      FR   Fi  F1  F2  F3  (382.8, 882.8) FRy 882.8   tan 1  tan 1  66.6o FRx 382.8 Vector moment chính: M RA   M A ( Fi ) 2 2  100  0  600  0.4  400 0.3  400 0.8 2 2  551 CHƯƠNG 2 Thu gọn hệ lực, điều kiện cân bằng 1. Định lý tương đương cơ bản Điểm đặt của lực chính để hệ không còn moment chính là M RA 551 d= = = 0.6m FR 962 d = 0.6m Giảng viên Nguyễn Duy Khương 6
  7. Khoa Khoa Học Ứng Dụng 9/7/2011 Bài giảng Cơ Học Ứng Dụng - Tuần 2 CHƯƠNG 2 Thu gọn hệ lực, điều kiện cân bằng 1. Định lý tương đương cơ bản Ví dụ 3: Thu gọn hệ lực về tâm O (phương  pháp giải tích) rC  (0, 0,1) rB  (0.15, 0.1,1)   F1  (0, 0, 800) F2  (250,166, 0)  M  (0, 400,300) Vector chính:     FR   Fi  F1  F2  ( 250,166, 800) Vector moment chính:     M RO   M ( F i )  M       M O ( F1 )  M O ( F2 )  M  (166, 250, 0)  (0, 400,300)  (166, 650,300) CHƯƠNG 2 Thu gọn hệ lực, điều kiện cân bằng 1. Định lý tương đương cơ bản Giảng viên Nguyễn Duy Khương 7
  8. Khoa Khoa Học Ứng Dụng 9/7/2011 Bài giảng Cơ Học Ứng Dụng - Tuần 2 CHƯƠNG 2 Thu gọn hệ lực, điều kiện cân bằng 1. Định lý tương đương cơ bản Ví dụ 3: Cho hình lập phương cạnh 1 đơn vị. Thu gọn hệ lực về tâm O z    F1  (0, 0,1) F2  (0, 1, 0) F3  (1, 0, 1)    2 r1  (0, 0, 0) r2  (1,1,1) r3  (0,1,1) 3     1 M O ( F1 )  r1  F1  (0, 0, 0) 1     O M O ( F2 )  r2  F2  (1, 0, 1) 2 y     M O ( F3 )  r3  F3  (1,1, 1)   x M 1  (1, 0, 1) M 2  (1, 1, 0)  Vector lực chính R   Fi  (1, 1, 0)     Vector moment chính M O   M O ( Fi )   M i  (0, 0, 3) CHƯƠNG 2 Thu gọn hệ lực, điều kiện cân bằng 1. Định lý tương đương cơ bản Thu gọn hệ lực để làm gì???    FR  0    HỆ CÂN BẰNG TĨNH  M RO  0   FR  FR  0    HỆ CÓ HỢP LỰC  M RO  0 Giảng viên Nguyễn Duy Khương 8
  9. Khoa Khoa Học Ứng Dụng 9/7/2011 Bài giảng Cơ Học Ứng Dụng - Tuần 2 CHƯƠNG 2 Thu gọn hệ lực, điều kiện cân bằng 1. Định lý tương đương cơ bản MR    FR  0 M RO F d HỆ TƯƠNG ĐƯƠNG    MỘT NGẪU  M RO  0 d       FR  0  M RO  0  FR .M RO  0 HỆ CÓ HỢP LỰC  M RO d   FR CHƯƠNG 2 Thu gọn hệ lực, điều kiện cân bằng 1. Định lý tương đương cơ bản       FR  0  M RO  0  FR .M RO  0 HỆ XOẮN Giảng viên Nguyễn Duy Khương 9
  10. Khoa Khoa Học Ứng Dụng 9/7/2011 Bài giảng Cơ Học Ứng Dụng - Tuần 2 CHƯƠNG 2 Thu gọn hệ lực, điều kiện cân bằng 1. Định lý tương đương cơ bản Tổng kết     FR  0  M RO  0  Hệ cân bằng tĩnh     FR  0  M RO  0  Hệ có hợp lực     FR  0  M RO  0  Hệ tương đương một ngẫu       FR  0  M RO  0  FR .M RO  0  Hệ có hợp lực       FR  0  M RO  0  FR .M RO  0  Hệ xoắn    FR  FR Hai hệ lực được gọi là tương đương    1   2  M O1  M O 2 CHƯƠNG 2 Thu gọn hệ lực, điều kiện cân bằng 1. Định lý tương đương cơ bản Bất biến của hệ lực Bất biến thứ nhất (BB1) là vector chính của hệ lực FR Bất biến thứ hai (BB2) là tích vô hướng của vector chính FR và vector moment chính MRO của hệ lực Dựa vào hai bất biến này ta sẽ tìm được dạng chuẩn (dạng tương đương tối giản) •BB1 0 và BB2=0 thì hệ là hệ có hợp lực •BB1 0 và BB2  0 thì hệ là hệ xoắn •BB1= 0 dẫn đến BB2 = 0 thì hệ là hệ cân bằng nếu vector moment chính bằng không và là hệ tương đương với ngẫu lực nếu vector moment chính khác không Giảng viên Nguyễn Duy Khương 10
  11. Khoa Khoa Học Ứng Dụng 9/7/2011 Bài giảng Cơ Học Ứng Dụng - Tuần 2 CHƯƠNG 2 Thu gọn hệ lực, điều kiện cân bằng 1. Định lý tương đương cơ bản Bài tập về nhà Cho hình lập phương cạnh 1 đơn vị. Thu gọn hệ lực về tâm O và tìm các tính  chất của hệ lực đó O O O O O CHƯƠNG 2 Thu gọn hệ lực, điều kiện cân bằng 2. Điều kiện cân bằng của hệ (Hệ 6 phương trình)  Fkx  0   Fky  0      Fkz  0 Hệ cân bằng tĩnh  FR  0  M R  0    mx ( Fk )  0 O  my ( Fk )  0   mz ( Fk )  0 Giảng viên Nguyễn Duy Khương 11
  12. Khoa Khoa Học Ứng Dụng 9/7/2011 Bài giảng Cơ Học Ứng Dụng - Tuần 2 CHƯƠNG 2 Thu gọn hệ lực, điều kiện cân bằng 2. Điều kiện cân bằng của hệ Hệ lực đặc biệt 1. Hệ lực phẳng  Fkx  0  Dạng 1  Fky  0 A là điểm bất kì trong mặt phẳng  m (F )  0  A k  Fka  0 A và B là hai điểm bất  Dạng 2  mA ( Fk )  0 kì trong mặt phẳng  m (F )  0 không trùng nhau  B k  mA ( Fk )  0  Dạng 3   mB ( Fk )  0 A, B, C không thẳng hàng  m (F )  0  C k CHƯƠNG 2 Thu gọn hệ lực, điều kiện cân bằng 2. Điều kiện cân bằng của hệ 2. Hệ lực đồng quy z F1 Trong ba chiều F3  Fkx  0   Fky  0  F 0 y   kz F2 x Trong hai chiều y F1  Fkx  0   Fky  0 F3 F2 x Giảng viên Nguyễn Duy Khương 12
  13. Khoa Khoa Học Ứng Dụng 9/7/2011 Bài giảng Cơ Học Ứng Dụng - Tuần 2 CHƯƠNG 2 Thu gọn hệ lực, điều kiện cân bằng 2. Điều kiện cân bằng của hệ Định lý bổ sung Nếu vật rắn tự do mà cân bằng dưới tác dụng của ba lực không song song nằm trên cùng một mặt phẳng, thì đường tác dụng của chúng cắt nhau tại một điểm Chứng minh F1 R F2 F3 CHƯƠNG 2 Thu gọn hệ lực, điều kiện cân bằng 2. Điều kiện cân bằng của hệ N A NB B A P NC B RA C A P Giảng viên Nguyễn Duy Khương 13
  14. Khoa Khoa Học Ứng Dụng 9/7/2011 Bài giảng Cơ Học Ứng Dụng - Tuần 2 CHƯƠNG 2 Thu gọn hệ lực, điều kiện cân bằng 2. Điều kiện cân bằng của hệ 3. Hệ lực song song z F3 Trong ba chiều  Fkz  0   M Ox  0 O.  M 0 y  Oy F1 F2 x Trong hai chiều a F3  Fka  0  O.  M O  0 F1 F2 CHƯƠNG 2 Thu gọn hệ lực, điều kiện cân bằng 2. Điều kiện cân bằng của hệ Giảng viên Nguyễn Duy Khương 14
  15. Khoa Khoa Học Ứng Dụng 9/7/2011 Bài giảng Cơ Học Ứng Dụng - Tuần 2 CHƯƠNG 2 Thu gọn hệ lực, điều kiện cân bằng 2. Điều kiện cân bằng của hệ Q N1 N2 N3 P CHƯƠNG 2 Thu gọn hệ lực, điều kiện cân bằng 2. Điều kiện cân bằng của hệ Ví dụ: Cho mô hình mối nối của cầu, tìm ẩn số lực C và T Điều kiện cân bằng của hệ lực đồng quy Cách 1 (chiếu lên hệ trục Oxy)  Fx  8  T cos 30o  C sin 20o  16  0   Fy  T sin 40  C cos 20  3  0 o o T  9, 09kN  C  3, 03kN Cách 2 (chiếu lên hệ trục Ox’y’)  Fx '  T  8cos 40  16 cos 40  3sin 40  C sin 20  0 o o o o   Fy '  C sin 20  3cos 40  8sin 40  16sin 40  0 o o o o Chỉ còn 1 ẩn ở phương trình 2!! Giảng viên Nguyễn Duy Khương 15
  16. Khoa Khoa Học Ứng Dụng 9/7/2011 Bài giảng Cơ Học Ứng Dụng - Tuần 2 CHƯƠNG 2 Thu gọn hệ lực, điều kiện cân bằng 2. Điều kiện cân bằng của hệ Ví dụ: Cho một thanh dầm nặng 100kg và kích thước như hình vẽ, nối sợi dây vào điểm C và kéo một lực P sao cho đầu B di chuyển lên độ cao 3m so với mặt đất. Tính lực kéo P và phản lực của mặt đất lên dầm tại điểm A. Điều kiện cân bằng của hệ lực song song  Fy  P  R  100 * 9,81  0   M A  P (6 cos  )  100 * 9,81(4 cos  )  0 3 Lưu ý: sin      22o 8  R  327 N   P  654 N CHƯƠNG 2 Thu gọn hệ lực, điều kiện cân bằng 2. Điều kiện cân bằng của hệ Ví dụ: Tìm phản lực liên kết Điều kiện cân bằng của hệ  Ay  320 N  Fkx   Bx  600 cos 45  0 o    Bx  424 N   Fky  By  Ay  200  100  600sin 45  0  B  405 N o  y  M  100  2  600sin 45o  5  600 cos 45o  0.2  A  7  0  B y Giảng viên Nguyễn Duy Khương 16
  17. Khoa Khoa Học Ứng Dụng 9/7/2011 Bài giảng Cơ Học Ứng Dụng - Tuần 2 CHƯƠNG 2 Thu gọn hệ lực, điều kiện cân bằng 2. Điều kiện cân bằng của hệ Ví dụ: Tìm phản lực liên kết Điều kiện cân bằng của hệ  Fkx  Ax  N B sin 30o  0  Ax  100 N    Fky  Ay  60  N B cos 30  0   Ay  233N o  M  90  60 1  N  0.75  0  N B  200 N  A B CHƯƠNG 2 Thu gọn hệ lực, điều kiện cân bằng 2. Điều kiện cân bằng của hệ Ví dụ: Cho dầm AC như hình vẽ, tại đầu C treo một bao cát nặng 80kg. Tính phản lực ngay tại A và lực căng dây tại B và E Ay T T Ax P Giảng viên Nguyễn Duy Khương 17
ADSENSE

CÓ THỂ BẠN MUỐN DOWNLOAD

LV.15: Bộ Đồ Án Tốt Nghiệp Chuyên Ngành Cơ Khí
65 tài liệu
2431 lượt tải
THÔNG TIN
TRỢ GIÚP
HỖ TRỢ KHÁCH HÀNG
Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.

 

Đồng bộ tài khoản
2=>2