Chương 4. Đối tượng điều chỉnh
Đối tượng điều chỉnh trong công nghiệp
72
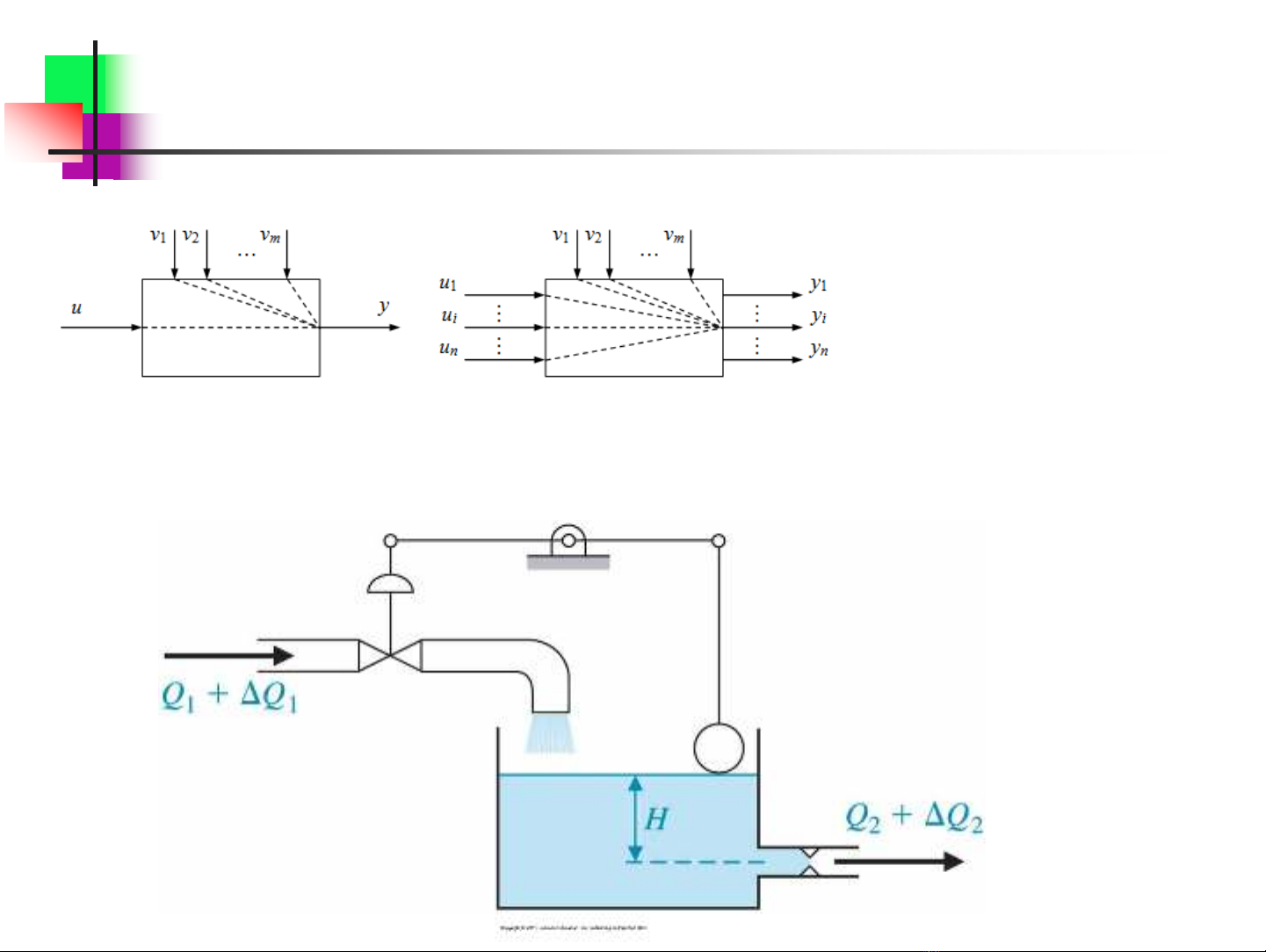
Đối tượng một đầu ra và đối tượng nhiều đầu ra
u : tác động điều chỉnh
v: chấn động (nhiễu)
y: tín hiệu ra

73
Khi thiết kế hệ thống cần:
Biết tính chất động học của đối tượng điều khiển ứng với mỗi
kênh tín hiệu vào, chọn ra những tác động điều khiển hiệu quả
nhất và kiểm soát những chấn động ảnh hưởng lớn.
Xây dựng mô hình của đối tượng cho từng kênh điều khiển
cũng như các kênh nhiễu.
Cần xác định sự thay đổi đặc tính động học của đối tượng
điều chỉnh do các chấn động bên trong gây ra
Chương 4. Đối tượng điều chỉnh
Đối tượng điều chỉnh trong công nghiệp (tiếp)
74
Chương 4. Đối tượng điều chỉnh
Đặc trưng các đối tượng công nghiệp
Quán tính
lớn
Trễ vận tải
Đặc trưng của
đối tượng công nghiệp
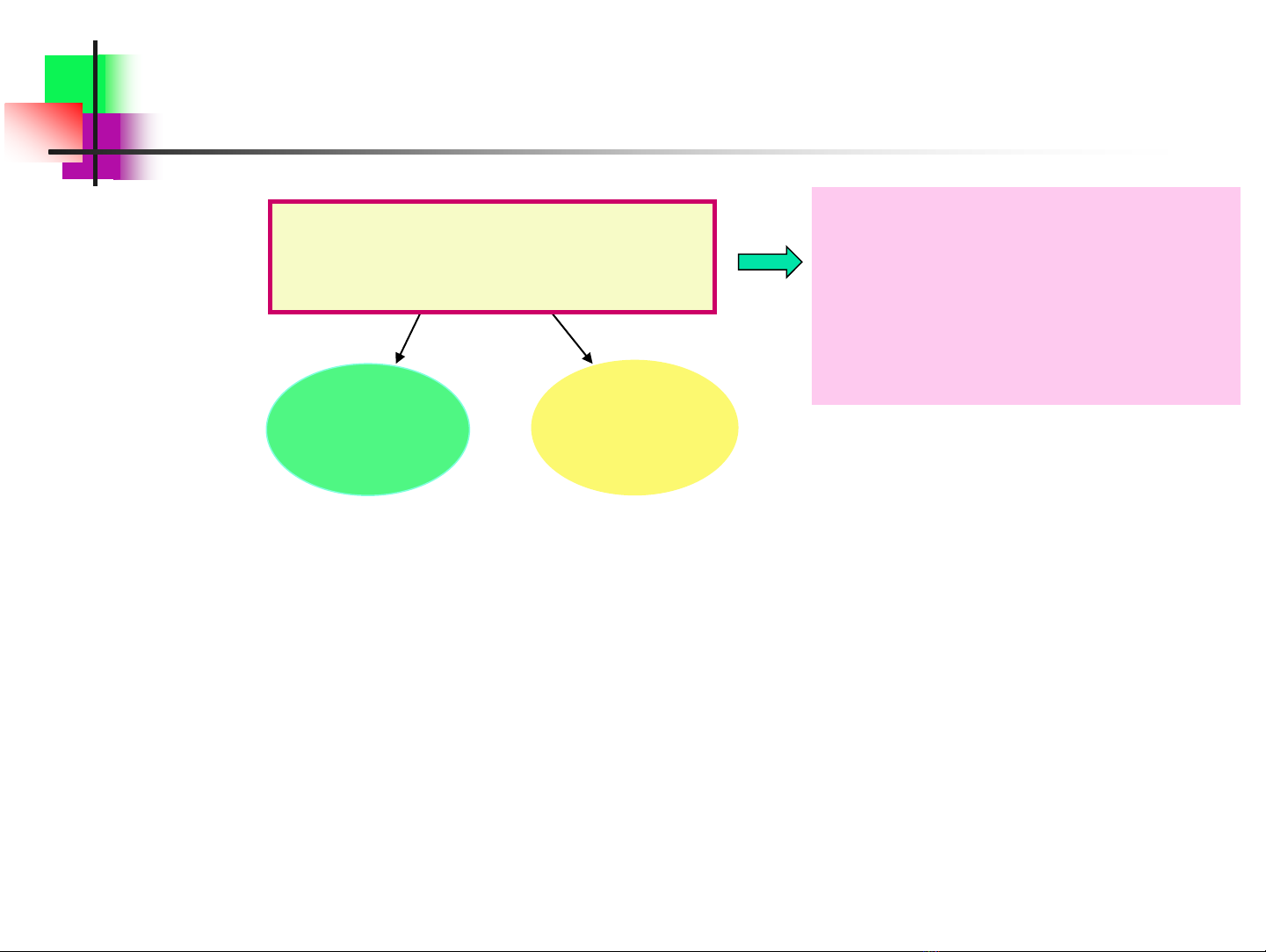
•Trễ vận tải còn gọi là trễ tuyệt đối, trễ thời gian chết (dead time), v,v…, đó là
thời gian kể từ thời điểm xuất hiện xung đầu vào (≠0) đến khi đại lượng ra
bắt đầu thay đổi so với giá trị xác lập ban đầu.
•Độ quán tính của đối tượng phản ánh mức độ chậm phản ứng của nó, kể từ
khi đại lượng ra đã bắt đầu thay đổi.
Hầu hết các đối tượng điều
khiển công nghiệp cũng như hệ
thống điều khiển tương ứng là
những bộ lọc tần số thấp
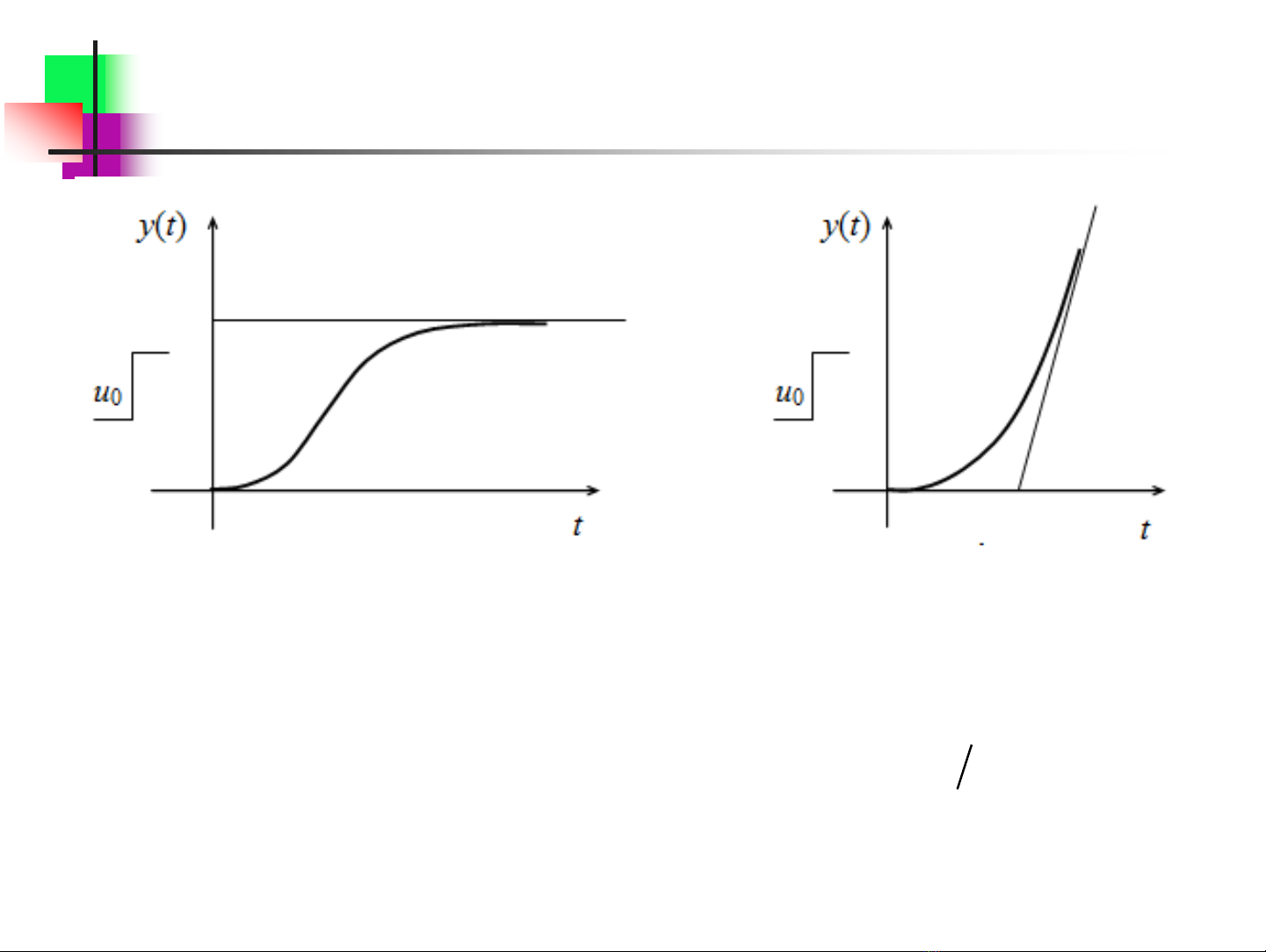
Đặc trưng: tốc độ biến thiên cực đại vmax và hệ số tĩnh học K∞
u0 là độ lớn xung bậc thang vào
y(∞) là giá trị xác lập đầu ra
75
Chương 4. Đối tượng điều chỉnh
Phân loại đối tượng công nghiệp
Đặc tính quá độ đặc trưng của
đối tượng tĩnh
Đặc tính quá độ đặc trưng của
đối tượng phi tĩnh
max 0 0
max '( ) / , ( )v y t u K y u
76
Chương 4. Đối tượng điều chỉnh
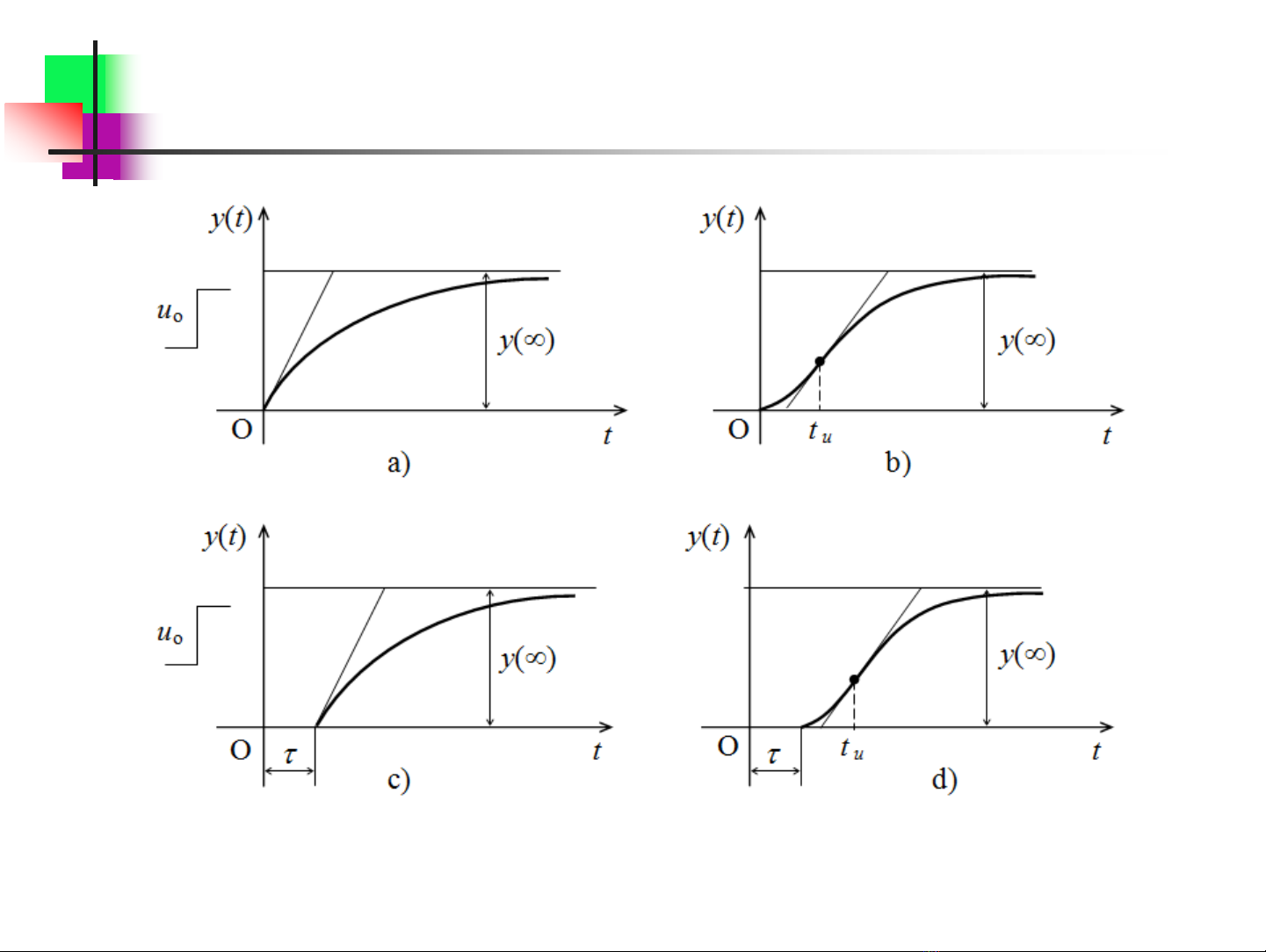
Mô hình đối tượng tĩnh (đối tượng có tự cân bằng)
Các dạng đặc tính quá độ của đối tượng có tự cân bằng







![Bài giảng Kỹ thuật nhiệt: Các quá trình của không khí ẩm - Trần Thị Thu Hằng [Chuẩn SEO]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250506/antrongkim0609/135x160/2371746505990.jpg)
![Bài giảng Kỹ thuật nhiệt: Các quá trình nhiệt động cơ bản của khí lý tưởng - Trần Thị Thu Hằng [Chuẩn Nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250506/antrongkim0609/135x160/221746505996.jpg)










![Ngân hàng trắc nghiệm Kỹ thuật lạnh ứng dụng: Đề cương [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251007/kimphuong1001/135x160/25391759827353.jpg)






